-
Notifications
You must be signed in to change notification settings - Fork 232
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
About the y_likelihoods #306
Comments
|
Please see the following two sections:
Briefly, each element of y is encoded using a probability distribution p. The y_likelihoods represent the value p(y).
|
|
Thank you for your reply! I really appreciate it!!I still have some issues to ask: |
|
|
Thank you so much! I have another question:how can I calculate the y_likelihoods if I don't use quantization(add uniform noise)(Because I want to apply it to my research domain) |
|
Sorry to bother you again.The element of y_likelihoods represents the value p(yi).Is p(yi) the probability that the symbol yi appears? If so,how is it ensured that the sum of the probabilities of all symbols appearing is equal to 1? |
|
For the But how is
|
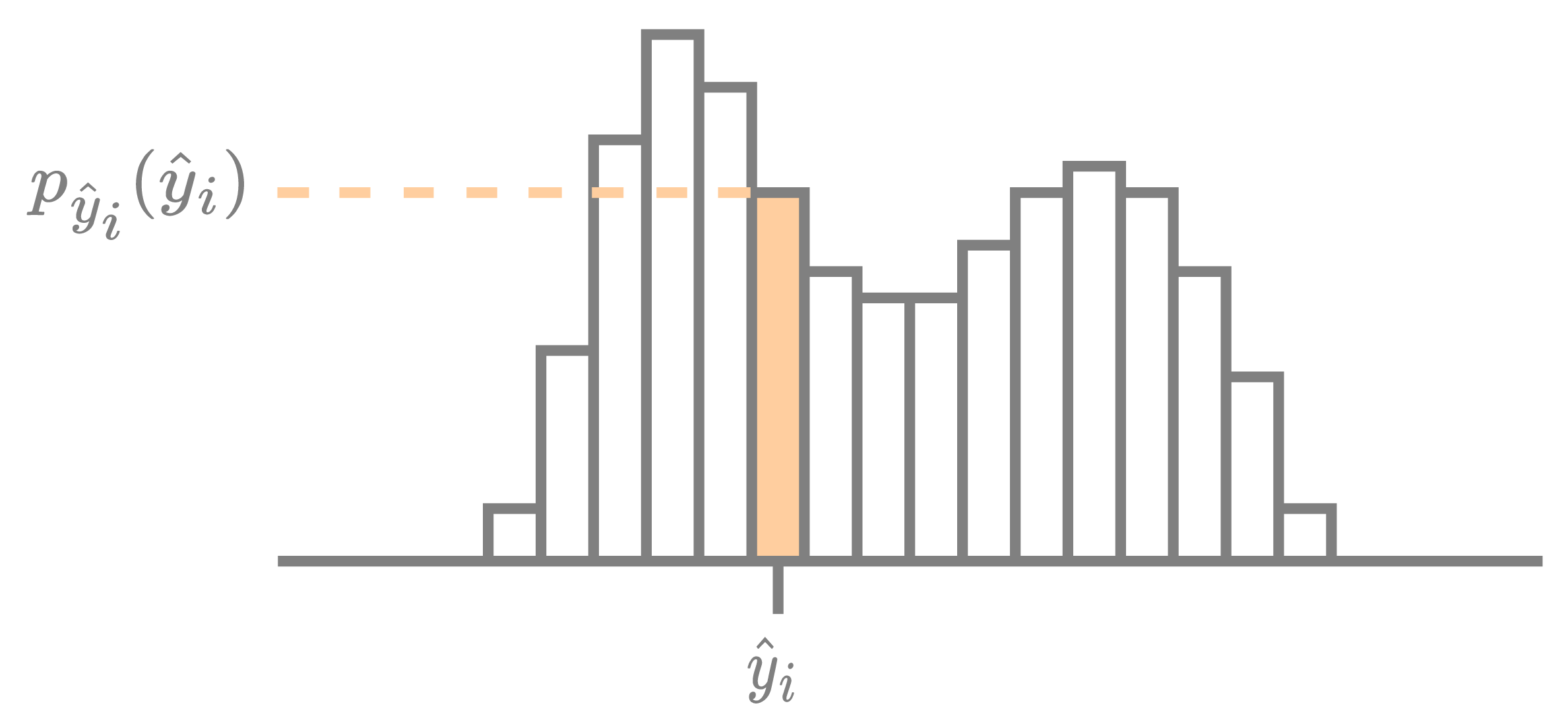
Sorry to bother you, I am recently been in the area of compression, take VARIATIONAL IMAGE COMPRESSION WITH A SCALE HYPERPRIOR as example, what is the meaning of each element in y_likelihoods matrix("likelihoods": {"y": y_likelihoods})?
The text was updated successfully, but these errors were encountered: