1424. Diagonal Traverse II

1424. Diagonal Traverse II (Medium)

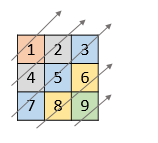
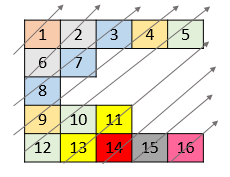
Given a list of lists of integers, nums, return all elements of nums in diagonal order as shown in the below images.

 

Example 1:

Input: nums = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,4,2,7,5,3,8,6,9]

Example 2:

Input: nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
Output: [1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]

Example 3:

Input: nums = [[1,2,3],[4],[5,6,7],[8],[9,10,11]]
Output: [1,4,2,5,3,8,6,9,7,10,11]

Example 4:

Input: nums = [[1,2,3,4,5,6]]
Output: [1,2,3,4,5,6]

 

Constraints:

• 1 <= nums.length <= 10^5
• 1 <= nums[i].length <= 10^5
• 1 <= nums[i][j] <= 10^9
• There at most 10^5 elements in nums.

Related Topics:
Array, Sort

Solution 1.

At each level, we can use two iteractors to scan the elements, the first one is the scanning iterator, and the second one is the end iterator.

When the scanning iterator meets the end iterator, this array is exhausted.

So we can use a list of iterator pairs, for each level:

• if there are new arrays to scan, add its begin and end iterator into the list
• For iterator pairs in the list, visit each of them and add the corresponding elements to the result.
• We add the updated iterator pair into the end of the list if the array is not exhausted.

// OJ: https://leetcode.com/problems/diagonal-traverse-ii/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
    typedef vector<int>::iterator iter;
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& A) {
        vector<int> ans;
        int i = 0, N = A.size();
        list<pair<iter, iter>> q;
        while (i < N || q.size()) {
            if (i < N) {
                q.emplace_front(A[i].begin(), A[i].end());
                ++i;
            }
            int cnt = q.size();
            while (cnt--) {
                auto p = q.front();
                q.pop_front();
                ans.push_back(*p.first);
                p.first++;
                if (p.first != p.second) q.emplace_back(p.first, p.second);
            }
        }
        return ans;
    }
};

Solution 2.

// OJ: https://leetcode.com/problems/diagonal-traverse-ii/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& A) {
        unordered_map<int, vector<int>> m;
        int N = A.size(), maxKey = 0, cnt = 0;
        for (int i = N - 1; i >= 0; --i) {
            int M = A[i].size();
            cnt += M;
            for (int j = M - 1; j >= 0; --j) {
                m[i + j].push_back(A[i][j]);
                maxKey = max(maxKey, i + j);
            }
        }
        vector<int> ans;
        ans.reserve(cnt);
        for (int i = 0; i <= maxKey; ++i) {
            for (int n : m[i]) ans.push_back(n);
        }
        return ans;
    }
};