1637. Widest Vertical Area Between Two Points Containing No Points

1637. Widest Vertical Area Between Two Points Containing No Points (Medium)

Given n points on a 2D plane where points[i] = [xi, yi], Return the widest vertical area between two points such that no points are inside the area.

A vertical area is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The widest vertical area is the one with the maximum width.

Note that points on the edge of a vertical area are not considered included in the area.

 

Example 1:

​

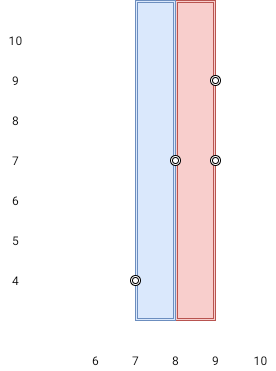
Input: points = [[8,7],[9,9],[7,4],[9,7]]
Output: 1
Explanation: Both the red and the blue area are optimal.

Example 2:

Input: points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]
Output: 3

 

Constraints:

• n == points.length
• 2 <= n <= 105
• points[i].length == 2
• 0 <= xi, yi <= 109

Related Topics:
Sort

Solution 1. Sort

Sort the points in ascending order of x values, then traverse to find the maximum distance of x values between adjacent points.

// OJ: https://leetcode.com/problems/widest-vertical-area-between-two-points-containing-no-points/
// Author: github.com/lzl124631x
// Time: O(NlogN)
// Space: O(1)
class Solution {
public:
    int maxWidthOfVerticalArea(vector<vector<int>>& A) {
        sort(begin(A), end(A), [](auto &a, auto &b) { return a[0]< b[0]; });
        int ans = 0;
        for (int i = 1; i < A.size(); ++i) ans = max(ans, A[i][0] - A[i - 1][0]);
        return ans;
    }
};