212. Word Search II

212. Word Search II (Hard)

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

 

Example 1:

Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2:

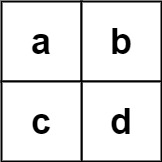
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

 

Constraints:

• m == board.length
• n == board[i].length
• 1 <= m, n <= 12
• board[i][j] is a lowercase English letter.
• 1 <= words.length <= 3 * 104
• 1 <= words[i].length <= 10
• words[i] consists of lowercase English letters.
• All the strings of words are unique.

Companies:
Amazon, Microsoft, Uber, Google, Cisco, Snapchat, Twitter, Apple, Oracle

Related Topics:
Array, String, Backtracking, Trie, Matrix

Similar Questions:

• Word Search (Medium)
• Unique Paths III (Hard)

Solution 1. Trie + Backtracking

Complexity Analysis

Building the Trie takes O(WL) time and O(WL) space, where W is the size of array words and L is the maximum length of a word.

The DFS part will take each point on the board as a starting point. There are O(MN) starting points. For each starting point, we DFS in 4 directions with the maximum depth being L. So the DFS part takes O(MN * 4^L) time.

// OJ: https://leetcode.com/problems/word-search-ii/
// Author: github.com/lzl124631x
// Time: O(WL + MN * 4^L) where M, N is the size of board, W is the size of words and L is the average length of word
// Space: O(WL)
struct TrieNode {
    TrieNode *next[26] = {0};
    bool word = false;
};
void addWord(TrieNode *node, string &w) {
    for (char c : w) {
        if (node->next[c - 'a'] == NULL) node->next[c - 'a'] = new TrieNode();
        node = node->next[c - 'a'];
    }
    node->word = true;
}
class Solution {
    int M, N, dirs[4][2] = {{0,1}, {0,-1}, {1,0}, {-1,0}};
    vector<string> ans;
    string path;
    void dfs(vector<vector<char>> &A, TrieNode *node, int x, int y) {
        char c = A[x][y];
        node = node->next[c - 'a'];
        if (!node) return;
        path.push_back(c);
        A[x][y] = 0;
        if (node->word) {
            ans.push_back(path);
            node->word = false; // prevent adding the same word again.
        }
        for (auto &dir : dirs) {
            int a = x + dir[0], b = y + dir[1];
            if (a >= M || a < 0 || b >= N || b < 0 || A[a][b] == 0) continue;
            dfs(A, node, a, b);
        }
        A[x][y] = c;
        path.pop_back();
    }
public:
    vector<string> findWords(vector<vector<char>>& board, vector<string>& words) {
        if (board.empty() || board[0].empty()) return {};
        M = board.size(), N = board[0].size();
        TrieNode root;
        for (auto &w : words) addWord(&root, w);
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) dfs(board, &root, i, j);
        }
        return ans;
    }
};

Solution 2. Trie + Backtracking

We mark visited end nodes using end = false to prevent re-adding the same word. But we still might waste time visting a subtree of Trie which doesn't have any valid words. To prevent such case, we can keep a counter cnt in the TrieNode. Whenever an end node is visited, we decrement the counter on it and on all its ancester nodes. In this way, when the counter is 0, we don't need to traverse the Trie subtree.

// OJ: https://leetcode.com/problems/word-search-ii/
// Author: github.com/lzl124631x
// Time: O(WL + MN * 4^L) where M, N is the size of board, W is the size of words and L is the average length of word
// Space: O(WL)
struct TrieNode {
    TrieNode *next[26] = {};
    int cnt = 0;
    bool end = false;
};
class Solution {
    TrieNode root;
    void addWord(TrieNode *node, string &s) {
        for (char c : s) {
            if (!node->next[c - 'a']) node->next[c - 'a'] = new TrieNode();
            node = node->next[c - 'a'];
            node->cnt++;
        }
        node->end = true;
    }
public:
    vector<string> findWords(vector<vector<char>>& A, vector<string>& words) {
        for (auto &s : words) addWord(&root, s);
        int M = A.size(), N = A[0].size(), dirs[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
        vector<string> ans;
        string tmp;
        function<int(int, int, TrieNode*)> dfs = [&](int x, int y, TrieNode *node) {
            int c = A[x][y] - 'a', cnt = 0;
            if (!node->next[c] || !node->next[c]->cnt) return 0;
            node = node->next[c];
            tmp.push_back(A[x][y]);
            if (node->end) {
                ans.push_back(tmp);
                ++cnt;
                node->end = false;
            }
            A[x][y] = 0;
            for (auto &[dx, dy] : dirs) {
                int a = x + dx, b = y + dy;
                if (a < 0 || a >= M || b < 0 || b >= N || A[a][b] == 0) continue;
                cnt += dfs(a, b, node);
            }
            A[x][y] = 'a' + c;
            tmp.pop_back();
            node->cnt -= cnt;
            return cnt;
        };
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) {
                dfs(i, j, &root);
            }
        }
        return ans;
    }
};