333. Largest BST Subtree

333. Largest BST Subtree (Medium)

Given the root of a binary tree, find the largest subtree, which is also a Binary Search Tree (BST), where the largest means subtree has the largest number of nodes.

A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties:

• The left subtree values are less than the value of their parent (root) node's value.
• The right subtree values are greater than the value of their parent (root) node's value.

Note: A subtree must include all of its descendants.

 

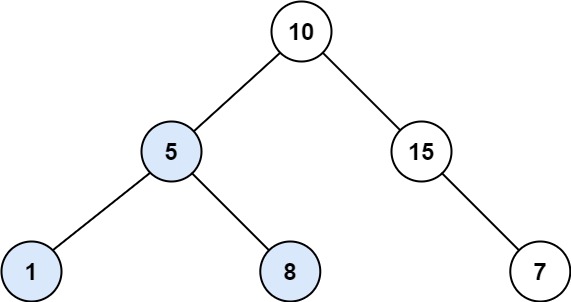
Example 1:

Input: root = [10,5,15,1,8,null,7]
Output: 3
Explanation: The Largest BST Subtree in this case is the highlighted one. The return value is the subtree's size, which is 3.

Example 2:

Input: root = [4,2,7,2,3,5,null,2,null,null,null,null,null,1]
Output: 2

 

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• -104 <= Node.val <= 104

 

Follow up: Can you figure out ways to solve it with O(n) time complexity?

Companies:
Amazon, ByteDance

Related Topics:
Dynamic Programming, Tree, Depth-First Search, Binary Search Tree, Binary Tree

Solution 1. Post-order Traversal

// OJ: https://leetcode.com/problems/largest-bst-subtree/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(H)
class Solution {
    int ans = 0;
    array<int, 3> dfs(TreeNode *root) { // min, max, count. If invalid, count = -1
        if (!root) return {INT_MAX,INT_MIN,0};
        auto left = dfs(root->left), right = dfs(root->right);
        bool valid = left[2] != -1 && right[2] != -1 && left[1] < root->val && right[0] > root->val;
        if (valid) ans = max(ans, 1 + left[2] + right[2]);
        return {left[2] ? left[0] : root->val, right[2] ? right[1] : root->val, valid ? 1 + left[2] + right[2] : -1};
    }
public:
    int largestBSTSubtree(TreeNode* root) {
        dfs(root);
        return ans;
    }
};