Skip to content

Latest commit

 

History

History
306 lines (164 loc) · 30.5 KB

casper_note.md

File metadata and controls

306 lines (164 loc) · 30.5 KB
Raw

Casper

下文是摘錄自 Vitalik 的 Casper note，若有看不懂的地方，可以對照原文

一個以保證金設計的權益證明演算法 (PoS)，目的是達到：

  1. 高度的最終安全
  2. 低成本的共識演算法

我們會描述該演算法，以及如何在異步網路中確保系統具備

  1. 安全性 (Safety)
  2. 活性 (Liveness)

以及描述保證金設計所帶來的賽局激勵

我們會描述在不同階段，設計的複雜度，並討論在此演算法中，驗證者 (Validator) 以及經濟激勵兩個特色。

背景

權益證明 (PoS) 已經發展一段時間，且被認為是有前景的，期望成為公有鏈上用來替代工作量證明 (PoW) 的共識演算法。

在 PoW 中，某一個 state 或某一段歷史的經濟共識是由量化計算資源來定義的。PoS 嘗試以 "Virtual mining"，虛擬挖礦的方式取代物理上的挖礦，即以 CPU、GPU 或 ASIC 挖礦的設備，而 PoS 對於經濟共識的定義，是靠系統內部的資源 (權益)，對某個特定的 state 或歷史去做承諾 (commit)。

然而，早期一些權益證明演算法存在一種缺陷，即 "Nothing at Stake"，沒有利害關係。如果只是很單純地用權益來產生區塊，當發生區塊不一致時，會不曉得如何處理鏈 A 或鏈 B 的選擇。這是由於在 PoS 之中不像 PoW，礦工必須集中算力來確保順利挖礦，進而對於鏈的選擇上，不會有模糊的空間。而在 PoS 之中，只要是理性的 validator，當看到不同的鏈時，他都能將權益押在不同的鏈上，確保兩邊都能得利，也就是所謂的"沒有利害關係"。

在 PoW 下，節點會集中算力押在 A，或是工作量最大的鏈

在 PoS 下，當節點看到兩個鏈，兩邊都押，有押有賺

Casper 的發展建立在引入 Slasher 的方法，企圖偵測這種模稜兩可的情況，(即拜占庭容錯問題中，同一人卻傳送了兩筆內容不同的訊息，在此，則指兩個鏈發生衝突)，並利用經濟懲罰的手段來遏止這種行為。

Casper 試圖規範節點只能押在一條鏈，否則進行懲罰

如此，便可以解決"沒有利害關係"的問題，並確保 PoS 可以比 PoW 來得更為安全。Vlad 指出過，建立在有懲罰機制上的共識算法，相比僅有獎勵機制的 PoW 共識算法更安全。因為系統會存在懲罰帶來的天生不對稱性，獎勵的多寡會限制有多少參與者的激勵，獎勵多少就是系統付出多少，而懲罰則是可擴大到整個權益池中所有人的權益。

這引入了一個新概念，"economic finality"，經濟的最終性。

一個區塊、一個狀態或是一段歷史，會被認為已成定局。假設在同個高度上，存在一個證明可以用於懲罰造假或有誤的另一方，並課以 X 等量的罰金，這個 X 值，被稱作加密經濟的邊際安全 (Cryptoeconomic Security Margin)。

然而，除了安全之外，PoS 還存在另一個可能的風險，就是當系統動彈不得的時候。例如下例之中，分別有各伴的 validator 分別對不同的區塊進行承諾，但是沒有任何一方勝出，就會造成系統卡住。

一個設計不良的算法或機制，在沒有懲罰或採取任何動作的情況下，很可能造成區塊無法完成被確認。

為了讓演算法能夠提供不可偽造的確認性，並要能夠避免系統發生動彈不得的情況，這是系統設計的一大挑戰。還好拜占庭容錯理論的發展已有一段時間，有些解決之道可用以借鏡。

演算法像是 PBFT、Paxos、HoneyBadger BFT 都嘗試在一群節點中(或是行程)，達到共識。早期該問題定義為參考拜占庭將軍問題，一群將軍計畫要攻下某座城，但是其中有些將軍是叛徒，目標是要達到：

  1. 忠誠的將軍會如實地執行既有計畫
  2. 小部分叛將不應該影響既有的決定

在現實中，共識算法中的"既有計畫"，可能是指操作的執行順序。

在區塊鏈的情形下，不是指共識能夠在一個回合中就被決定。而是必須經過多個回合，且在不停增長的鏈上達成共識。

在區塊鏈中，每一個區塊內的 hash 值，都會參照到前一個區塊的 hash，所以天生上，會連同過去的紀錄一直參照到創世區塊，達到共識。某種程度上，會與祖宗區塊 (ancestor block) 一同達到共識。因此共識演算法，應該避免不只是某段時間內，相互衝突的區塊；同時還要避免，當某區塊已經與某區塊達成共識，卻與其祖宗區塊發生衝突的狀況。

接著，我們將以 "Minimal Slashing Condition" 作為 PBFT 之外的替代演算法進行系統設計。

Minimal Slashing Conditions (最小懲罰條件)

在 Casper 中，假設底層存在一種提案機制 (proposal mechanism)，能夠產生持續增長的塊鏈，對於給定一組區塊，有個決定性的方式計算什麼是鏈的"尖端"。鏈可能很完美的增長，每隔幾秒一個區塊會被加到鏈的頂部，也有可能鏈會"分叉"，例如在某個母區塊往上分叉長出兩個子區塊，但其中一個子區塊最後會被棄置x，也有可能鏈的增漲情形是混亂的，需要多個回合來辨識哪個區塊才是鏈的頂部，以維持鏈的一致性。

產生這種"品質良好"區塊的提案機制，並不是安全性的必要因素。只要超過三分之二的節點正確地遵循協定，有衝突的檢查點 (checkpoint) 就不會被確認，僅管區塊的提案機制品質很差。然而，如果區塊的提案機制運行的很糟糕，會影響到系統的活性 (liveness)。

提案機制刻意保持抽象化。它可以是一個獨裁者，它可以是一個循環方案 (round-robin scheme)，由參與者彼此協商方式，又或是像我們的 Casper，採混合式的架構，由原始的工作量證明來提供區塊。

鏈上每一百個區塊，被稱作檢查點 (checkpoint)，兩個檢查點之間的稱作一個時期 (epoch)。我們假設存在好幾組驗證者 V1, ..., Vn，每一組的驗證者數量為 S(V1), ..., S(Vn)，在混合式的權益證明中，參與的驗證者必須放置保證金。保證金的數量相當於他們的大小。

驗證者有能力傳送兩種類型的訊息：

  1. [PREPARE, epoch, hash, epoch_source, hash_source]
  2. [COMMIT, epoch, hash]

目的是為了在每個時期 (epoch=n)，驗證者等待提案機制，來產生在 epoch=n 時的檢查點，且其 hash=H，首先驗證者會發送他的看法，PREPARE 訊息伴隨 epoch n 與 hash H。而 epoch_source 及 hash_source 會參考到最近一次的檢查點(epoch x)，該檢查點收到 prepare 數量來自 PREPSET 中的驗證者，且數量超過所有驗證者的三分之二。

sum_{v in PREPSET} S(V) >= sum_{v in ALL_VALIDATORS} S(V) * 2/3

如果有至少三分之二的驗證者發起 (epoch=n, hash=H) 的 PREPARE，並且他們的 epoch_source 及 hash_source 是相同的，驗證者就會發送 COMMIT 來提交 n 與 H。若得到超過三分之二的人支持，則這個檢查點就被確認 (finalized)。

雖然我們認為驗證者"應該"要遵循這樣的機制，但我們無法強迫他們。舉例來說，考慮當提案機制的區塊產生分叉時，並產生在 epoch=n 時，有兩個競爭的檢查點，C1 和 C2。假設有個驗證者在 C2 來之前的前 5 秒先看到 C1，則那個驗證者按規則會預備看到 C1 的訊息。然而，如果驗證者先預備 C2，我們無法偵測，因為 C1 的訊息可能因為延遲了 6 秒才送到該驗證者的電腦，導致他先看到 C2。

有可能因為延遲造成訊息收到的順序不一致

然而我們能做的就是，判別驗證者有明顯違規的狀況，並且狠狠的處罰他們，甚至拿到他們的保證金。

我們定義"懲罰條件"，當驗證者觸發這些條件的時候，他們會喪失所有的保證金。

並且，我們想要證明這個機制的兩個特性：

  1. 可咎責的安全 (Accountable safety)：如果兩個衝突的哈希被確認，肯定的是至少有三分之一的驗證者違反規則
  2. 看似可行的活性 (Plausible liveness)：除非有三分之一的人違反懲罰條件，否則必須存在有三分之二以上的驗證者，能夠發送確認某個哈希的訊息

詳細的機器驗證可參看 Isabelle，簡略的證明如下：

假設兩個衝突的哈希 C1 及 C2 被確認，這表示，在某個 epoch=e1 的時期， C1 拿到超過三分之二的 prepare 以及 commit，並在某個 epoch=e2 的時期，C2 拿到超過三分之二的 prepare 以及 commit。

考慮簡單的情形，當 e1=e2，那麼 C1 與 C2 同時有三分之二的 prepare，表示有三分之一的驗證者違反了 NO_DBL_PREPARE，他們重複在同一時期送出兩次不同的 prepare。又或是令一種狀況，如果有驗證者沒拿到超過三分之二的 prepare，則違反 PREPARE_REQ。

不失一般性，考慮 e2 > e1 的狀況，因為有 PREPARE_REQ 的限制，表示在 C2，有三分之二的驗證者在 e2' < e2 的時期做了 prepare，同理，可以回推到 e2" 的時期，直到遇到下列兩種條件停止：

  1. e2*=e1：表示有三分之二的人在 C1 與在某個 C2 的祖宗時期做了 prepare，其中有三分之一的人違反了 NO_DBL_PREPARE，重複發送 prepare 訊息。
  2. e2*<e1：有三分之二的 prepare 發生在 e1 之後的 e2，他的 epoch_source < e1，並且有三分之二的 commmit 在 e2 時期，其哈希與 e1 的相同。因此，至少有三分之一的預備者違反了 PREPARE_COMMIT_CONSISTENCY。

看似可行的活性的證明較簡單。假設：

  1. P 是最新的 epoch 時期且有三分之二以上的 prepare
  2. M 是最新的 epoch 時期，且任何訊息都已經送出

因為 (1) 我們知道沒有任何誠實的 commit 高過 P，表示有三分之二的驗證者可以在 M+1 的時期安全地做預備，且其 epoch_source 為 P，可以安全地被提交。

補充

由下列文章補充一些說明

為了達到 1) 容錯; 2) 異步安全; 3) 密碼經濟共識，Casper 的目標關鍵在於達到"經濟確認"。假設區塊 B1 被確認，那麼 a) B1 永遠是鏈的一部分; b) 對於導致 B1 被撤銷的人，會被課以 至少 X 價值的處罰，我們需要要求驗證者繳交保證金來完成"經濟確認"，某種程度上可視作 Authenticated Byzantine General，這也有益我們沒收他的保證金，而這些驗證者，對於區塊的確認，則可視作"經濟確認"，而對於違反保證金機制來確認區塊的人，定義了一些懲罰條件 ("Slashing conditions")。

懲罰條件可以看作

如果一個驗證者簽署了一份如下的訊息:

["PREPARE", epoch, HASH1, epoch_source1]

以及另一份他簽署的訊息

["PREPARE", epoch, HASH2, epoch_source2]

我們可以觀察到 Hash1 != Hash2 或是 epoch_source1 != epoch_source2，但是 epoch 的值在兩個訊息當中是相同的，那麼他的保證金就會被沒收。

有人在同一時間送了兩份不同的聲明，那他的保證金就該被沒收

為了處理這樣的懲罰條件，協定定義了一些懲罰條件，如果誠實的遵循規則運作就不會觸發懲罰條件，反之，同一時間送出兩次 PREPARE 訊息被抓到，就會被處罰。

"PREPARE" 與 "COMMIT" 這兩個單詞，是由傳統的拜占庭容錯共識理論借來的。在這，想像他們是兩種不同型式的訊息，之後在協定中，你可在想成共識需要由兩個回合的協議來達成，"PREPARE" 用於第一回合，"COMMIT" 用於第二回合。

另外，需要定義確認條件 (finality condition)，表示驗證者能夠決定某個特定的哈希值會被確認。

當有哈希值在某一個時期 (epoch) 被確認，會存在一種形式的訊息如下：

["COMMIT", epoch, HASH]

如果將送出如上 COMMIT 訊息的驗證者的保證金加總，會得到的金額總數約佔了總有保證金的三分之二以上。簡言之，有三分之二的驗證者對這個哈希值進行承諾。

懲罰條件需要滿足兩個條件：

  1. 可咎責的安全 (Accountable safety)：有人不守規矩，要能抓到他們，消減他們。
  2. 看似可行的活性 (Plausible liveness)：除了要保證低於三分之一的人不違反規則，還必須有三分之二的驗證者要能夠送出 COMMIT，確保系統不會動彈不得。有人作怪，剔除他，並保證踢完他後系統能正常運作。

有四類的懲罰條件：

懲罰條件一：[COMMIT_REQ]

當驗證者送出簽名後的 COMMIT 訊息，如果沒看到他之前對於該 Hash 的 PREPARE，且該 PREPARE 有其他超過三分之二的驗證者聲明，那他就違反懲罰條件。

送出 ["COMMIT", epoch, HASH] 之前，要有其他三分之二的人包含他自己，聲明 ["PREPARE", epoch, HASH, epoch_source]

懲罰條件二：[PREPARE_REQ]

當驗證者送出簽名後的 PREPARE 訊息，如果在這之前，他在某個時期也有送出 PREPARE，但屬於不同時期，則除非該 PREPARE 也有超過三分之二的人聲明，他才能夠送出對於新的時期的 PREPARE 聲明，否則他就違反懲罰條件。

送出 ["PREPARE", epoch, HASH, epoch_source] 之前，要確認之前的聲明 ["PREPARE", epoch_source, ANCESTOR_HASH, epoch_source_source] 有其他三分之二的人也同樣聲明

懲罰條件三：[PREPARE_COMMIT_CONSISTENCY]

當驗證者送出簽名後的 COMMIT 訊息，未來他的 PREPARE 訊息中，不應該包含較 COMMIT 早的 epoch 時期，，否則他就違反懲罰條件。因為這明顯 PREPARE 與 COMMIT 的順序不一致。

送出 ["COMMIT", epoch1, HASH1] 後，若未來的聲明中 ["PREPARE", epoch2, HASH2, epoch_source]，時間序不一致 epoch_source < epoch1 < epoch2，不論哈希值是否衝突，都算違反條件。

懲罰條件四：[NO_DBL_PREPARE]

當驗證者送出簽名後的 PREPARE 訊息，並且同一時期他有兩份不同聲明，他明顯違反懲罰條件

單一時期內，不應該見到兩份訊息來自同一個驗證者

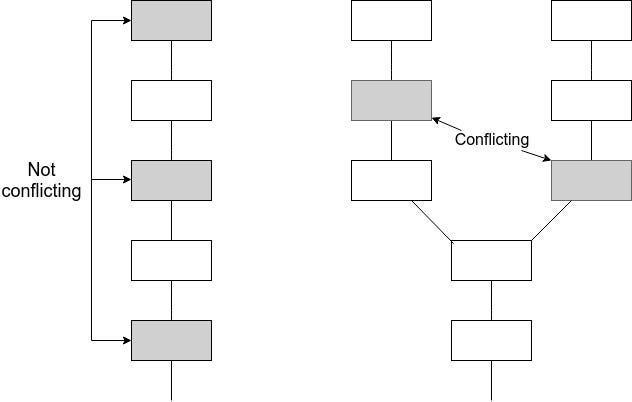
值得注意的是，有可能兩個不同的哈希值同時被確認，如果他們都是過去紀錄裡的一部分。事實上，在一個持續增長的鏈當中，會有越來越多的哈希被確認，而那是我們想要達到的結果。

下圖裡，左邊的鏈當中，可能同時有三個不同的哈希值被確認，但不衝突，因為他們都是鏈的一部分，而在右圖中，當鏈出現分叉後，不應該在分叉的情況下，同時有兩個不同的哈希值在不同的鏈上被確認。

回來看經濟確認，我們需要一個池來記錄驗證者。並且，驗證者可以自由地加入，一段時間後，需要投放保證金，且任何的參與者可以自由地離開，並在較長的一段時間後，可以領回他們的保證金。並且，這些驗證者可以簽署以下的訊息：

  1. ["PREPARE", epoch, HASH, epoch_source]
  2. ["COMMIT", epoch, HASH]

如果某個時期的哈希值，能夠蒐集到足夠的 COMMIT，那麼這個哈希值就被確認。哈希之間會鏈在一起，新的哈希會參照先前的哈希，我們期待有一個持續增長的鏈，新的哈希會不停近來，且被確認。而對於遵循這套機制的驗證者，給予經濟獎勵。

你可以將這個模型，視作在 PBFT 之中，具備 "live under synchrony, safe under asynchrony" 這樣的特性，只是透過懲罰條件來達到可咎責的安全與看似可行的活性。

這個想法啟發自 PBFT 與 Tendermint 的綜合，但模型定義不同，可能會有不同的結果。

值得注意的是，看似可行的活性與實際的活性有所不同。看似可行的活性指的是，理論上我們能夠進行確認，但是我們需要一個提案機制 (proposal mechanism)，要有人不停地提出哈希，這樣 PREPARE 與 COMMIT 才能運行，並被確認。提案機制可能會故障，懲罰條件必須能夠確認他故障，且不會有安全失敗的風險。

我們可以結合懲罰條件與其他不同的提案機制，只要他們滿足少數條件：

  1. 存在一種提案機制，會在每個時期都提出一個有效的(合法的)哈希值
  2. 哈希值會形成鏈的形式
  3. 提案的哈希值不應該讓懲罰條件無法確認

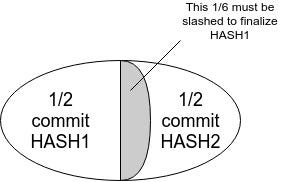
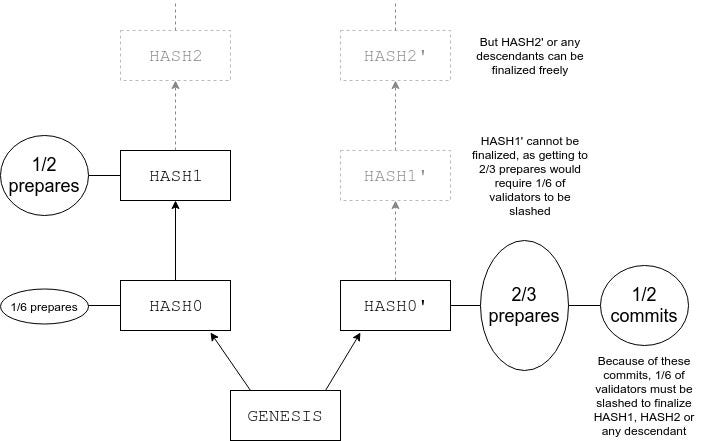
考慮一種狀況，如下圖，我們有個提案機制在 epoch=0 時，提出 Hash0，在 epoch=1 時，提出 Hash1，Hash1 指向 Hash0，但在某種緣故下，沒有任何足夠的 PREPARE 來達成 COMMIT。此外，因為故障的原因，提案機制對 epoch=0 提出 Hash0'，這使得 Hash0' 獲得三分之二的聲明，二分之一的提交。

現在，提案機制可能發生兩種狀況，一種是繼續生成 Hash2 和 Hash3，但沒有哈希會被提交，除非有六分之一的人被懲罰條件給消減。另一種情形是，提案機制繼續提出 Hash1'，但 Hash1' 無法被確認，因為 Hash1 掌握了二分之一的 prepare 所以他無法拿超過三分之二，提案機制繼續提出 Hash2'，而這次 Hash2' 有可能被終結，提案機制會繼續提案繼續運作。

另外一種想法是，有沒有可能利用傳統的最長鏈規則來解決上述的問題？

最長鏈規則也不一定能夠完整運作，就上圖，按最長鏈規則會等待 Hash2 而不是 Hash1'，這會造成鏈永遠也無法被確認，解決這樣的狀況，不一定需要有人被削減，只要礦工能夠商量好繼續在 Hash0' 下進行，因此我們提出"修改版本的分叉選擇規則" (modified fork choice rule)。

  1. 從創世的 HEAD 開始執行
  2. 找到 HEAD 的有效子孫，並且有超過三分之二的 PREPARE 與最大數量的 COMMIT
  3. 將 HEAD 設為那個有效子孫的哈希，並回到第二步
  4. 當第二步找不到滿足的條件時，採用區塊鏈底層的分叉選擇規則 (最長鏈，GHOST 或其他) 來找初鏈的頂部

在這樣修改後的版本，Hash0' 比起 Hash1 更有利成為鏈的頂部，這也滿足我們想要的行為。

上述懲罰規則，使得要反轉確認的區塊變得成本昂貴。但還有一些型態的錯誤或故障，沒有涵蓋在本文中，想是確認無效的哈希，或是在已經確認的哈希之中，有些資料無法存取。最簡單的方式，就是下載所有的區塊來進行驗證，就可以忽略那些無效的哈希。

決定一個特定的哈希是否被確認有兩個步驟

  1. 檢查是否有三分之二的提交
  2. 檢查鏈是否有效

個人看法

  1. 要在保證金還在的時期內，完成經濟確認
  2. 要在驗證者的保證金還被鎖在合約當中，對他們的不當行為進行偵測與懲罰
  3. 當驗證者不在線上，要有能力激勵他們回來工作

什麼是 Proof of Stake

權益證明 (Proof of Stake, PoS) 是公有鏈共識演算法的一類，以太坊接下來的 Casper 演算法也是其中之一。它和比特幣、目前的以太坊及許多其他區塊鏈背後的工作量證明 (Proof of Work) 有著相似的作用 - 鞏固鏈的安全，但在安全性及能源使用效率上有著更顯著的優點。

總的來說，PoS 演算法大致如下。區塊鏈上會保持追蹤著一組驗證者 (Validator)，任何持有該區塊鏈原幣 (以太坊而言，指的是以太幣) 的人，都可藉由一個特殊交易鎖住他們的以太幣當作押金，成為驗證者。同意新區塊產生的過程會透過一個共識演算法來完成，而所有的驗證者都能夠參與這個過程。

有許多的共識演算法以及方式來指派獎勵給參與共識算法的驗證者，因此 PoS 有許多調料。從演算法的角度，主要分為兩種：鏈形式的權益證明以及拜占庭容錯 (Byzantine Fault Tolerance, BFT) 形式的權益證明。

在鏈形式的權益證明中，演算法會每隔一段時間 (例如十秒一個間隔)，以偽隨機的方式挑選一個驗證者，並賦予該驗證者擁有建立一個區塊的權利，而這個區塊必須指向前一個區塊 (正常來說為最長鏈的最新區塊)，所以隨著時間，區塊會收斂成一條持續增長的鏈。

在拜占庭容錯形式的權益證明中，一群驗證者會隨機被指派來提出區塊，但是同意以那一個區塊為標準，需要經過多個回合，在每一輪當中，每一個驗證者會投票給特定的區塊，最後一輪的時候，所有的 (誠實以及在線上的) 驗證者會一致同意，任何被指定到的區塊是屬於鏈的一部分。注意區塊仍然會被鏈在一起，主要的差異在，一個區塊的共識來自一個區塊的時間內，而不是依靠鏈的長度或大小來決定。

權益證明相較於工作量證明有哪些優勢？

這篇文章 - 權益證明的設計哲學：A Proof of Stake Design Philosophy，有更完整的論述。

簡短來說：

  • 不需要為了鏈的安全而消耗大量電力，（估計以太坊和比特幣每天都會各消耗一百萬美元在電力及硬體成本上）。
  • 因為不需要消耗大量電力，所以沒有發行較多新貨幣的需求，來提供參與者加入網路的動機。理論上甚至可能有負的淨發行量，因為有部分交易手續費不見了，所以供應量隨時間而減少。
  • 權益證明打開更廣泛的技術大門，使用賽局理論與機制設計來避免集權卡特爾的形成，以及當他們的組織會危害到網路。(例如，工作量證明中的自私挖礦 (selfish mining))。
  • 減少中心化造成的風險，當經濟規模不是一個問題。相比一百萬貨幣，一千萬的貨幣讓你獲得高於十倍的報酬，沒有額外不成比例的收益，越有錢你能買得起越多大規模的生產設備。
  • 利用經濟懲罰來提高不同形式的 51% 攻擊成本，更勝於工作量證明的實行，引用 Vlad Zamfir 的話，"想像一參與 51% 攻擊，你的 ASIC 工廠就被燒毀"。

權益證明如何套用到傳統的拜占庭容錯研究？

拜占庭容錯研究有一些重要的結論，可以應用到所有共識算法，包括傳統的共識算法像是 PBFT，也可以是任何的權益證明演算法，以及有適當數學模型的工作量證明。

重要結論包含：

  • CAP 理論 - "在網路分區發生的情況下，必須選擇一致性或可用性，系統無法同時滿足"。簡單直觀的論點：如果網路分成兩區 (partition)，在其中一區我送了一筆交易"將我的十元給 A"，另一區送另一筆交易"將我的十元給 B"。若是系統無法服務，可能單筆或兩筆交易都無法被處理；也可能系統中的資料變得不一致，其中一個分區看到的是第一筆交易的結果，另一個分區看到的是第二筆交易的結果。注意 CAP 理論與擴展性 (scalability) 無關，同樣適用於分片 (sharded) 與非分片系統。"
  • FLP 不可能性 - 在非同步 (asynchronous) 的設定中 (即正常運作的節點間都無法保證網路的延遲)，即使存在一個故障/惡意節點，都無法保證系統在有限時間下達成一致。值得注意的是，"Las Vegas" algorithms不在其中，該演算法在每一輪 (T 秒) 皆有一定機率達成共識，而隨著 T 值增加，機率會越趨近於 1，這是許多成功的共識演算法會採用的突破口。
  • 容錯上限 - 由 DLS paper，我們知道： 1）在部分同步 (partially synchronous) 的網路環境中 (即網路延遲有上限，但我們無法事先知道是多少)，協議可以容忍最多 1/3 的節點故障 (即拜占庭故障)。 2）在非同步 (asynchronous) 的網路環境中，具確定性的協議 (deterministic protocol) 無法容忍任何錯誤，但這篇論文並沒有提及隨機演算法(randomized algorithms) 在這種情況可以容忍最多 1/3 的故障節點。 3）在同步 (synchronous) 的網路環境中 (即網路延遲已知並小於 d)，協議可以容忍 100% 的節點故障，但超過半數的節點都故障，會有一些條件限制。要注意的是，"認證過的拜占庭將軍 (authenticated Byzantine)" 模型是值得考慮的，不是"一般的拜占庭模型"；認證的部分，基本上是指我們可以將公私鑰加密用於我們的演算法當中，現在已有大量研究且計算成本低廉。

工作量證明已被 Andrew Miller 及他人嚴格的分析過，並應用在依賴於同步網路模型的算法中。我們可以將網路模型設為具有接近無窮數量的節點數，每個節點代表一個很小的計算單元，在給定的時間下生成區塊的機率非常低。在這個模型中，協定有 50% 的容錯率且假設沒有延遲，在這樣的觀察條件下，以太坊和比特幣分別有將近 46% 及 49.5% 的容錯率，但若網路延遲相當於區塊產生的時間時，容錯率會下降到 33%，如果網路延遲為無限大，容錯率為零。

權益證明的共識算法非常適合用在拜占庭容錯的共識模型，由於所有的驗證者有已知身份 (固定的以太坊地址)，且網路能夠追蹤驗證者集合的大小。權益證明的研究一般可分為兩個路線，一個是同步的網路模型，一個是部分非同步的網路模型。鏈型式的權益證明演算法，幾乎都仰賴同步的網路模型，其安全性分析相似於工作量證明的安全証明。另一個權益證明的研究路線是將傳統拜占庭容錯共識與部分同步網路相結合，解釋較為複雜，在後面的章節會有更深入的細節。

工作量證明和鏈形式的權益證明演算法，選擇資料的可用性而非一致性，但拜占庭容錯形式的共識算法更傾向於選擇資料一致性。Tendermint 很清楚地選擇一致性，而 Casper 採混合模型，更偏好資料的可用性，但也盡可能地確保資料的一致性，讓鏈上的應用與使用者知道在任何指定的時間內，當前的資料一致性有多大保證。

在 Ittay Eyal 和 Emin Gun Sirer 對於 自私挖礦 的發現中， - 在不同網路環境的模型中，比特幣挖礦的激勵兼容性（incentive compatibility）分別受到 25% 及 33% 的限制，即只有在 25% 或 33% 的礦工同謀不可能發生的前提下，挖礦的機制才是激勵兼容的（即礦工按照正常的方式挖礦--有多少算力獲得多少報酬）。這個結論和傳統的共識演算法的結論無關，因為傳統共識演算法的結論並沒有牽涉到激勵兼容性。

什麼是"缺乏利害關係"問題且該如何解決？

早期有許多 (都是鏈型態的) 權益證明演算法，包含 Peercoin，只有對區塊的產生給予獎勵而沒有懲罰。這造成一個不幸的後果，在有多條競爭鏈的情況下，驗證者會嘗試立即在每條鏈上都產生新區塊，只是要確定:

而在工作量證明中，這麼做會導致算力切半且無利可圖：

結果是，如果所有參與者都有這麼狹隘的經濟理性 (narrowly economically rational)，即使不存在任何攻擊者，區塊鏈本身也無法達成共識。如果存在攻擊者，攻擊者只要壓制那些無私心的節點 (永遠壓在原始鏈)，不需理會理性節點 (同時壓在原始鏈以及攻擊者的鏈)，相比工作量證明，攻擊者必須同時壓制無私心與理性的節點。 (或至少是有效威脅，請見P + epsilon 攻擊)

有些人認為利益關係人會有動機守規則且只壓在最長鏈上，為的是要"保存他們的投資"，然而這忽略考慮這動機會遭受公有地悲劇問題 (tragedy of the commons)：每位利益關係人可能只有 1% 的機會成為關鍵 (即他的參與影響攻擊的成敗)，所以說服他們參與攻擊的賄賂金只需要是他們的押金的 1%。因此，總共需要的賄賂金額僅佔所有押金的 0.5-1%。

此外，這個論點意味著任何零機會失敗的情況都不是一個穩定的平衡，好像失敗的機會是零，那麼每個人都有0％的機會是關鍵。

有些人會認為下注者有動機按照規則來下注且只下注在最長的鏈上，好讓他們的投資能夠保值，然而這個論點忽略了這個動機受制於公地悲劇理論（tragedy of the commons）：每個下注者可能只會有 1% 的機會成為關鍵的（pivotal）角色（即他的決定會影響一個攻擊的成敗），所以用來買通他們的賄絡金額只需要是他們總賭注金額的 1% 。因此，全部的賄賂金額只需要下注金額總額的 0.5-1% 。此外，這個（本段開頭的）論點同時暗示著任何"不可能失敗"的情況都不是一個穩定的平衡，因為不可能失敗的情況代表每個下注者成為關鍵角色的機會是零，即只要賄賂金額超過 0% 都能讓下注者有動機參與攻擊。