DSIN全称是Deep Session Interest Network(深度会话兴趣网络), 重点在这个Session上,这个是在DIEN的基础上又进行的一次演化,这个模型的改进出发点依然是如何通过用户的历史点击行为,从里面更好的提取用户的兴趣以及兴趣的演化过程,这个模型就是从user历史行为信息挖掘方向上进行演化的。而提出的动机呢? 就是作者发现用户的行为序列的组成单位,其实应该是会话(按照用户的点击时间划分开的一段行为),每个会话里面的点击行为呢? 会高度相似,而会话与会话之间的行为,就不是那么相似了,但是像DIN,DIEN这两个模型,DIN的话,是直接忽略了行为之间的序列关系,使得对用户的兴趣建模或者演化不是很充分,而DIEN的话改进了DIN的序列关系的忽略缺点,但是忽视了行为序列的本质组成结构。所以阿里提出的DSIN模型就是从行为序列的组成结构会话的角度去进行用户兴趣的提取和演化过程的学习,在这个过程中用到了一些新的结构,比如Transformer中的多头注意力,比如双向LSTM结构,再比如前面的局部Attention结构。
DSIN模型全称叫做Deep Session Interest Network, 这个是阿里在2019年继DIEN之后的一个新模型, 这个模型依然是研究如何更好的从用户的历史行为中捕捉到用户的动态兴趣演化规律。而这个模型的改进动机呢? 就是作者认为之前的序列模型,比如DIEN等,忽视了序列的本质结构其实是由会话组成的:
这是个啥意思呢? 其实举个例子就非常容易明白DIEN存在的问题了(DIN这里就不说了,这个存在的问题在DIEN那里说的挺详细了,这里看看DIEN有啥问题),上一篇文章中我们说DIEN为了能够更好的利用用户的历史行为信息,把序列模型引进了推荐系统,用来学习用户历史行为之间的关系, 用兴趣提取层来学习各个历史行为之间的关系,而为了更有针对性的模拟与目标广告相关的兴趣进化路径,又在兴趣提取层后面加了注意力机制和兴趣进化层网络。这样理论上就感觉挺完美的了啊。这里依然是把DIEN拿过来,也方便和后面的DSIN对比:
但这个模型存在个啥问题呢? 就是只关注了如何去改进网络,而忽略了用户历史行为序列本身的特点, 其实我们仔细想想的话,用户过去可能有很多历史点击行为,比如[item3, item45, item69, item21, .....], 这个按照用户的点击时间排好序了,既然我们说用户的兴趣是非常广泛且多变的,那么这一大串序列的商品中,往往出现的一个规律就是在比较短的时间间隔内的商品往往会很相似,时间间隔长了之后,商品之间就会出现很大的差别,这个是很容易理解的,一个用户在半个小时之内的浏览点击的几个商品的相似度和一个用户上午点击和晚上点击的商品的相似度很可能是不一样的。这其实就是作者说的homogeneous和heterogeneous。而DIEN模型呢? 它并没有考虑这个问题,而是会直接把这一大串行为序列放入GRU让它自己去学(当然我们其实可以人工考虑这个问题,然后如果发现序列很长的话我们也可以分成多个样本哈,当然这里不考虑这个问题),如果一大串序列一块让GRU学习的话,往往用户的行为快速改变和突然终止的序列会有很多噪声点,不利于模型的学习。
所以,作者这里就是从序列本身的特点出发, 把一个用户的行为序列分成了多个会话,所谓会话,其实就是按照时间间隔把序列分段,每一段的商品列表就是一个会话,那这时候,会话里面每个商品之间的相似度就比较大了,而会话与会话之间商品相似度就可能比较小。作者这里给了个例子:
这是某个用户过去的历史点击行为,然后按照30分钟的时间间隔进行的分段,分成了3段。这里就一下子看出上面说的那些是啥意思了吧。就像这个女生,前30分钟在看裤子,再过30分钟又停留在了化妆品,又过30分钟,又看衣服。这种现象是非常普遍的啊,反映了一个用户通常在某个会话里面会有非常单一的兴趣但是当过一段时间之后,兴趣就会突然的改变。这个时候如果再统一的考虑所有行为就不合理了呀。这其实也是DSIN改进的动机了, DSIN,这次的关键就是在S上。
那它要怎么改呢? 如果是我们的话应该怎么改呢? 那一定会说,这个简单啊,不是说DIEN没考虑序列本身的特点吗? 既然我们发现了上面用户点击行为的这种会话规律,那么我们把序列进行分段,然后再用DIEN不就完事了? 哈哈, 那当然可以呀, 如果想用DIEN的话确实可以这么玩, 但那样就没有新模型了啊,那不还是DIEN? 这样的改进思路是没法发顶会的哟哈哈。 下面分析下人家是怎么改进的。
简单的说是用了四步,这个也是DSIN模型的整体逻辑:
-
首先, 分段这个是必须的了吧,也就是在用户行为序列输入到模型之前,要按照固定的时间间隔(比如30分钟)给他分开段,每一段里面的商品序列称为一个会话Session。 这个叫做会话划分层
-
然后呢,就是学习商品时间的依赖关系或者序列关系,由于上面把一个整的行为序列划分成了多段,那么在这里就是每一段的商品时间的序列关系要进行学习,当然我们说可以用GRU, 不过这里作者用了多头的注意力机制,这个东西是在多个角度研究一个会话里面各个商品的关联关系, 相比GRU来讲,没有啥梯度消失,并且可以并行计算,比GRU可强大多了。这个叫做会话兴趣提取层
-
上面研究了会话内各个商品之间的关联关系,接下来就是研究会话与会话之间的关系了,虽然我们说各个会话之间的关联性貌似不太大,但是可别忘了会话可是能够表示一段时间内用户兴趣的, 所以研究会话与会话的关系其实就是在学习用户兴趣的演化规律,这里用了双向的LSTM,不仅看从现在到未来的兴趣演化,还能学习未来到现在的变化规律, 这个叫做会话交互层。
-
既然会话内各个商品之间的关系学到了,会话与会话之间的关系学到了,然后呢? 当然也是针对性的模拟与目标广告相关的兴趣进化路径了, 所以后面是会话兴趣局部激活层, 这个就是注意力机制, 每次关注与当前商品更相关的兴趣。
所以,我们细品一下,其实DSIN和思路和DIEN的思路是差不多的,无非就是用了一些新的结构,这样,我们就从宏观上感受了一波这个模型。接下来,研究架构细节了。 看看上面那几块到底是怎么玩的。
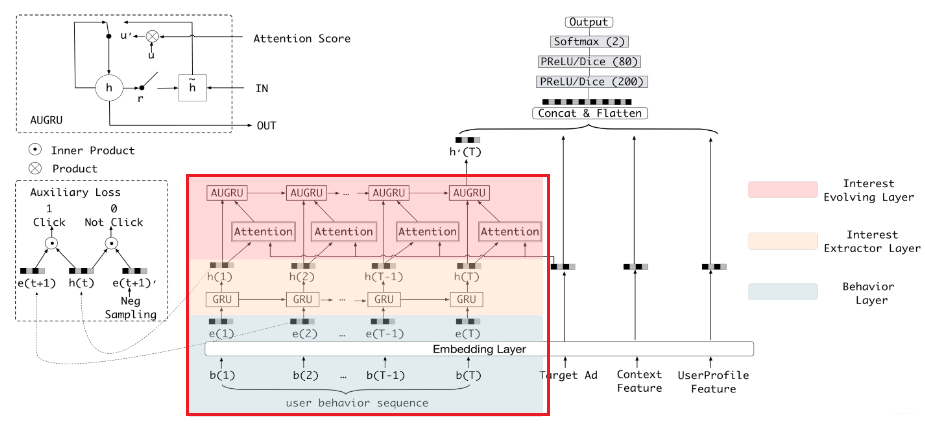
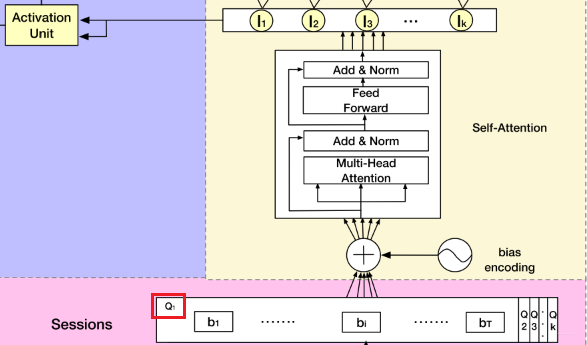
这里在说DSIN之前,作者也是又复习了一下base model模型架构,这里我就不整理了,其实是和DIEN那里一模一样的,具体的可以参考我上一篇文章。直接看DSIN的架构:
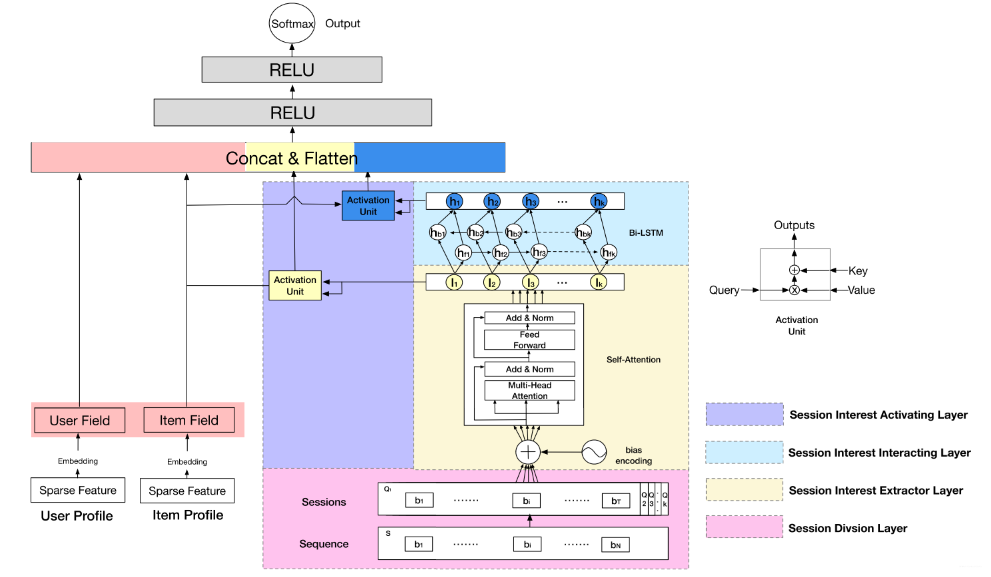
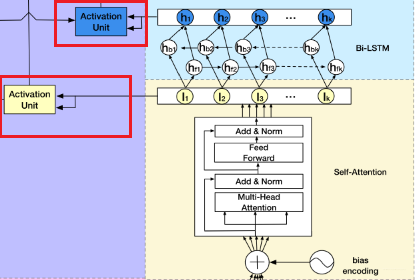
这个模型第一印象又是挺吓人的。核心的就是上面剖析的那四块,这里也分别用不同颜色表示出来了。也及时右边的那几块,左边的那两块还是我们之前的套路,用户特征和商品特征的串联。这里主要研究右边那四块,作者在这里又强调了下DSIN的两个目的,而这两个目的就对应着本模型最核心的两个层(会话兴趣提取层和会话交互层):
这一层是将用户的行为序列进行切分,首先将用户的点击行为按照时间排序,判断两个行为之间的时间间隔,如果前后间隔大于30min,就进行切分(划一刀), 当然30min不是定死的,具体跟着自己的业务场景来。
划分完了之后,我们就把一个行为序列$\mathbf{S}$转成了Sessions
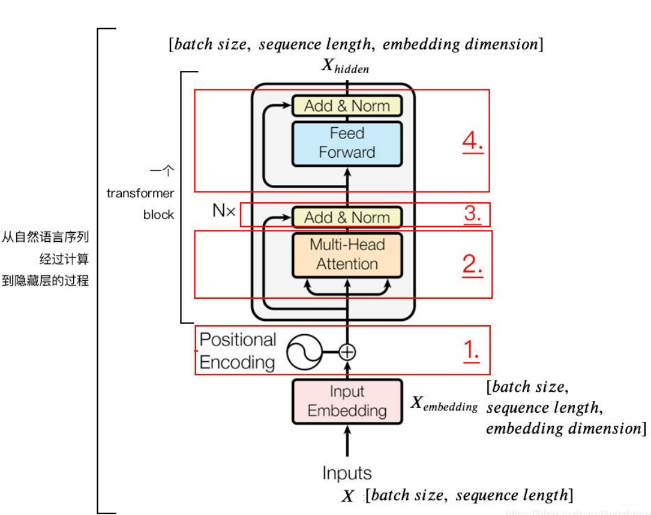
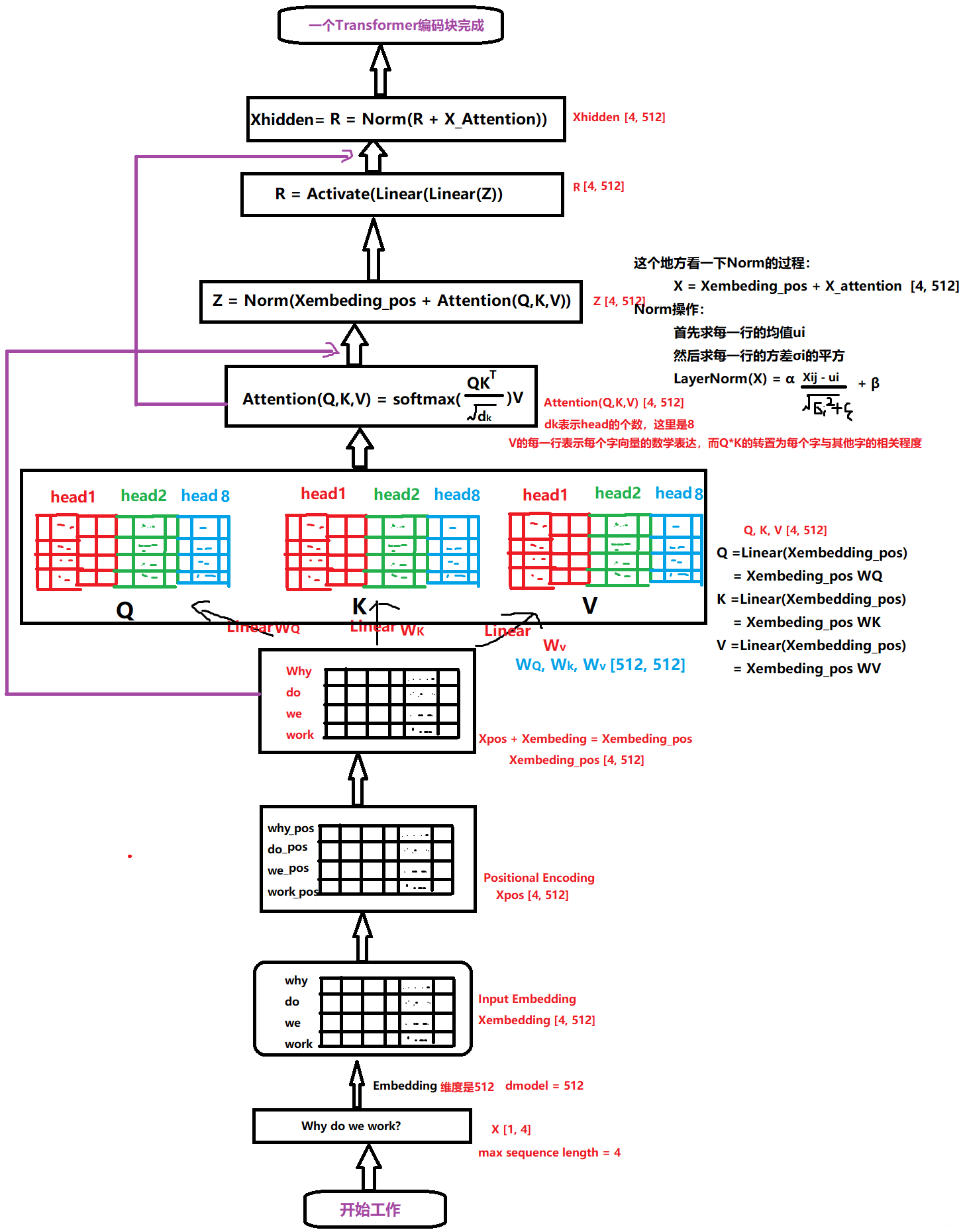
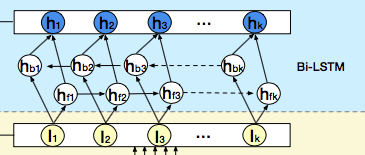
这个层是学习每个会话中各个行为之间的关系,之前也分析过,在同一个会话中的各个商品的相关性是非常大的。此外,作者这里还提到,用户的随意的那种点击行为会偏离用户当前会话兴趣的表达,所以为了捕获同一会话中行为之间的内在关系,同时降低这些不相关行为的影响,这里采用了multi-head self-attention。关于这个东西, 这里不会详细整理,可以参考我之前的文章。这里只给出两个最核心关键的图,有了这两个图,这里的知识就非常容易理解了哈哈。
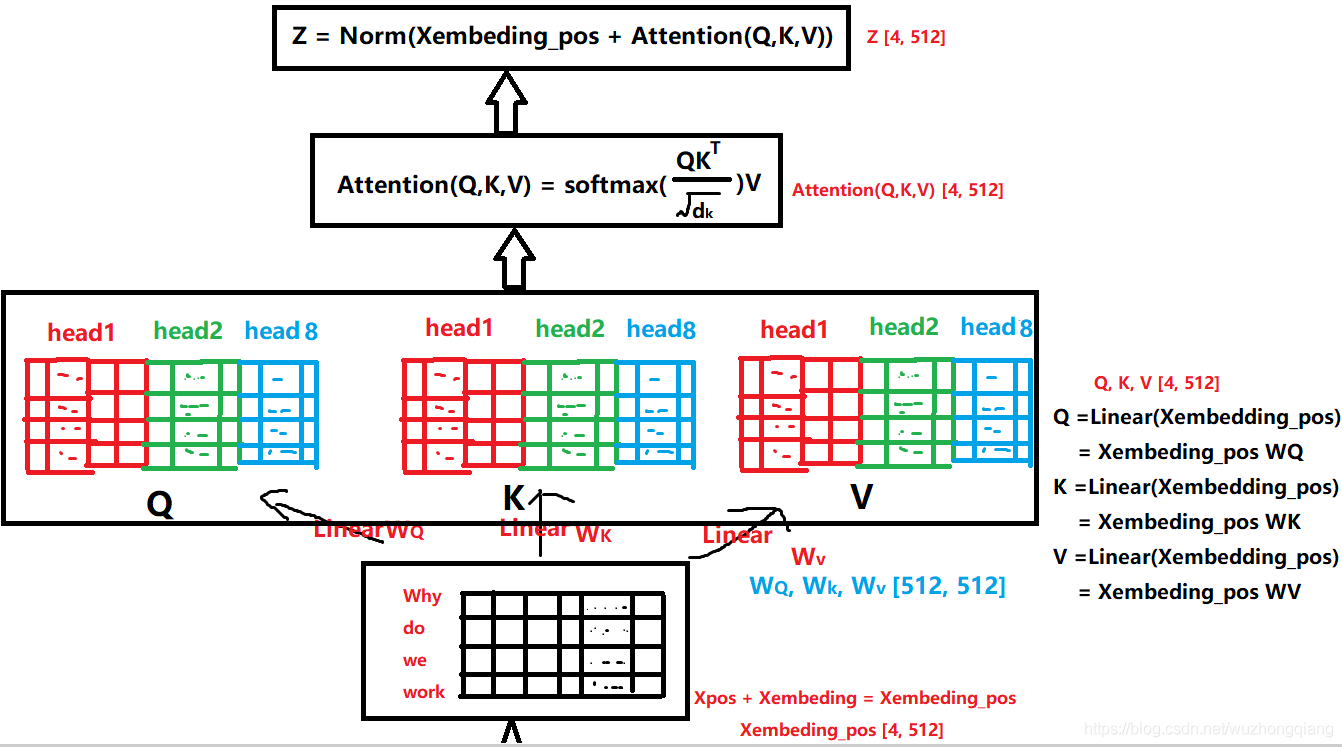
第一个,就是Transformer的编码器的一小块:
拿过来是为了更好的对比,看DSIN的结构的第二层,其实就是这个东西。 而这个东西的整体的计算过程,我在之前的文章中剖析好了:
有了上面这两张图,在解释这里就非常好说了。
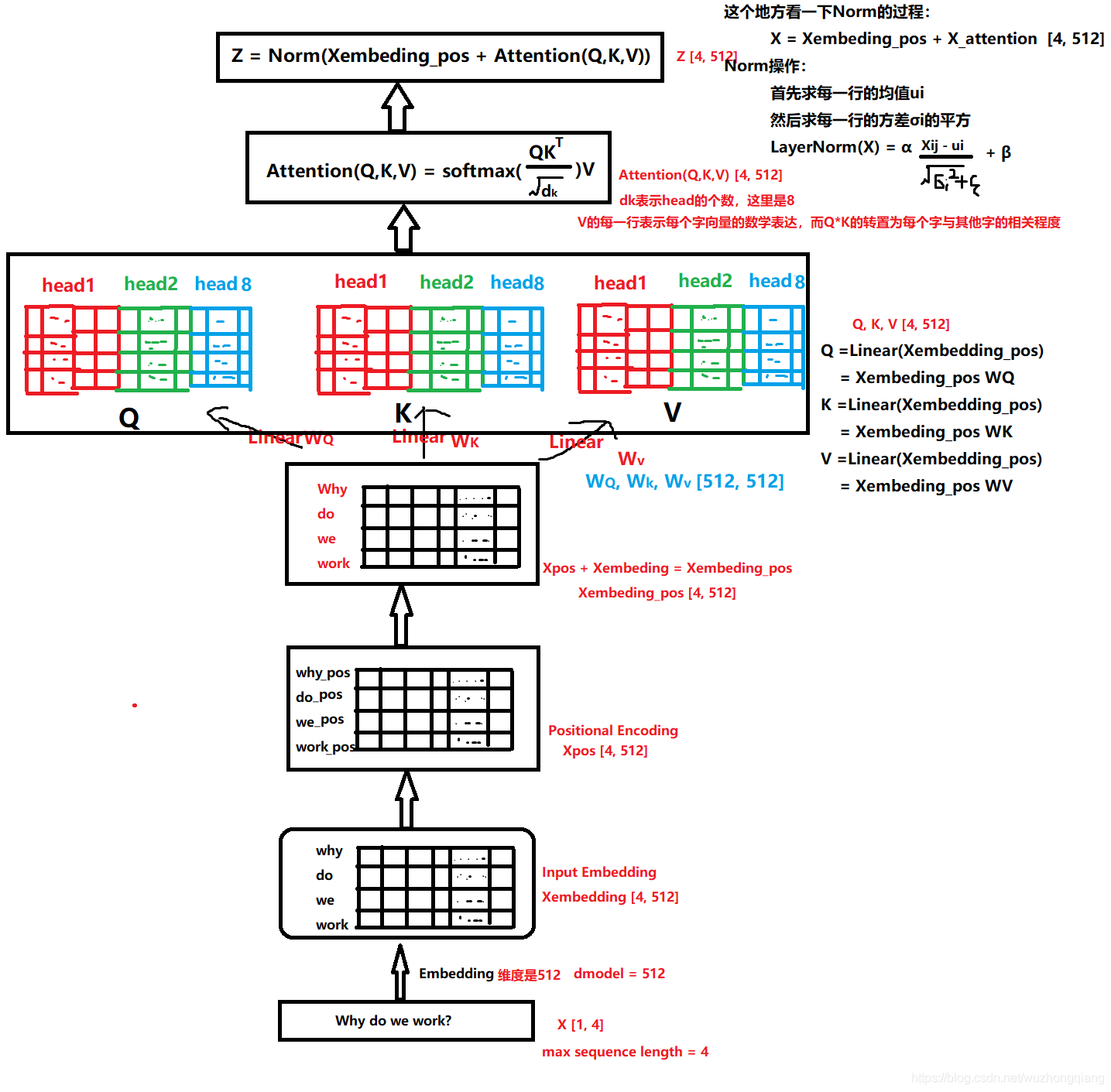
这一块其实是分两步的,第一步叫做位置编码,而第二步就是self-attention计算关联。 同样,DSIN中也是这两步,只不过第一步里面的位置编码,作者在这里做了点改进,称为Bias Encoding。先看看这个是怎么做的。
这里先解释下为啥要进行位置编码或者Bias Encoding, 这是因为我们说self-attention机制是要去学习会话里面各个商品之间的关系的, 而商品我们知道是一个按照时间排好的小序列,由于后面的self-attention并没有循环神经网络的迭代运算,所以我们必须提供每个字的位置信息给后面的self-attention,这样后面self-attention的输出结果才能蕴含商品之间的顺序信息。
在Transformer中,对输入的序列会进行Positional Encoding。Positional Encoding对序列中每个物品,以及每个物品对应的Embedding的每个位置,进行了处理,如下:
上式中$pos$指的是某个会话里面item位于第几个位置位置, 取值范围是$[0, max_len]$,
而这里,作者并不是用的这种方式,这是因为在这里还需要考虑各个会话之间的位置信息,毕竟这里是多个会话,并且各个会话之间也是有位置顺序的呀,所以还需要对每个会话添加一个Positional Encoding, 在DSIN中,这种对位置的处理,称为Bias Encoding。
于是乎作者在这里提出了个$\mathbf{B E} \in \mathbb{R}^{K \times T \times d_{\text {model }}}$,会发现这个东西的维度和会话分割层得到的$\mathbf{Q}$的维度也是一样的啊,其实这个东西就是这里使用的位置编码。那么这个东西咋计算呢? $$ \mathbf{B} \mathbf{E}{(k, t, c)}=\mathbf{w}{k}^{K}+\mathbf{w}{t}^{T}+\mathbf{w}{c}^{C} $$ $\mathbf{B} \mathbf{E}{(k, t, c)}$表示的是第$k$个会话中,第$t$个物品在第$c$维度这个位置上的偏置项(是一个数), 其中$\mathbf{w}^{K} \in \mathbb{R}^{K}$表示的会话层次上的偏置项(位置信息)。如果有$n$个样本的话,这个应该是$[n, K, 1, 1]$的矩阵, 后面两个维度表示的$T$和$emb _dim$。$\mathbf{w}^{T} \in \mathbb{R}^{T}$这个是在会话里面时间位置层次上的偏置项(位置信息),这个应该是$[n, 1, T, 1]$的矩阵。$\mathbf{w}^{C} \in \mathbb{R}^{d{\text {model }}}$这个是embedding维度层次上的偏置(位置信息), 这个应该是$[n, 1, 1, d_{model}]$的矩阵。 而上面的$\mathbf{w}{k}^{K},\mathbf{w}{t}^{T},\mathbf{w}{c}^{C}$都是表示某个维度上的具体的数字,所以$\mathbf{B} \mathbf{E}{(k, t, c)}$也是一个数。
所以$\mathbf{B} \mathbf{E}$就是一个$[n,K, T, d_{model}]$的矩阵(这里其实是借助了广播机制的),蕴含了每个会话,每个物品,每个embedding位置的位置信息,所以经过Bias编码之后,得到的结果如下: $$ \mathbf{Q}=\mathbf{Q}+\mathbf{B} \mathbf{E} $$ 这个$\mathbf{Q}$的维度$[n,K, T, d_{model}]$, 当然这里我们先不考虑样本个数,所以是$[K, T, d_{model}]$。相比上面的transformer,这里会多出一个会话的维度来。
接下来,就是每个会话的序列都通过Transformer进行处理:
一定要注意,这里说的是每个会话,这里我特意把下面的$Q_1$框出来了,就是每个$Q_i$都会走这个自注意力机制,因为我们算的是某个会话当中各个物品之间的关系。这里的计算和Transformer的block的计算是一模一样的了, 我这里就拿一个会话来解释。
首先$Q_1$这是一个$T\times embed _dim$的一个矩阵,这个就和上面transformer的那个是一模一样的了,细节的计算过程其实是一样的。
这里在拿过更细的个图来解释,首先这个$Q_1$会过一个多头的注意力机制,这个东西干啥用呢? 原理这里不说,我们只要知道,这里的头其实是从某个角度去看各个物品之间的关系,而多头的意思就是从不同的角度去计算各个物品之间的关系, 比如各个物品在价格上啊,重量上啊,颜色上啊,时尚程度上啊等等这些不同方面的关系。然后就是看这个运算图,我们会发现self-attention的输出维度和输入维度也是一样的,但经过这个多头注意力的东西之后,就能够得到当前的商品与其他商品在多个角度上的相关性。怎么得到呢?
拿一个head来举例子:
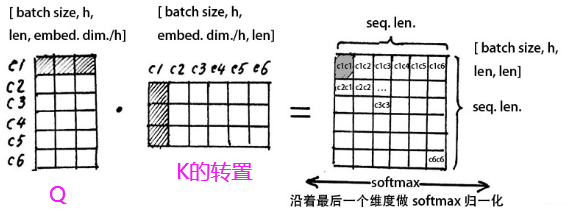
我们看看这个$QK^T$在表示啥意思:
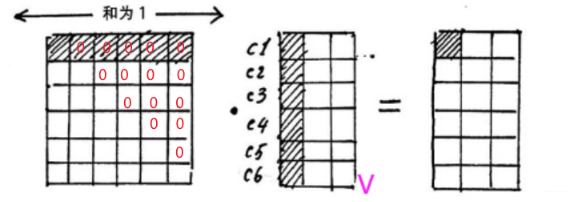
假设当前会话有6个物品,embedding的维度是3的话,那么会看到这里一成,得到的结果中的每一行其实表示的是当前商品与其他商品之间的一个相似性大小(embedding内积的形式算的相似)。而沿着最后一个维度softmax归一化之后,得到的是个权重值。这是不是又想起我们的注意力机制来的啊,这个就叫做注意力矩阵,我们看看乘以V会是个啥
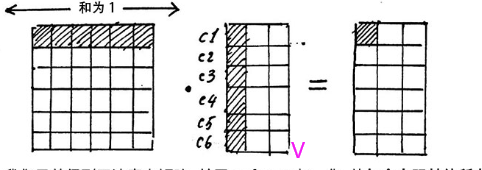
这时候,我们从注意力矩阵取出一行(和为1),然后依次点乘V的列,因为矩阵V的每一行代表着每一个字向量的数学表达,这样操作,得到的正是注意力权重进行数学表达的加权线性组合,从而使每个物品向量都含有当前序列的所有物品向量的信息。而多头,不过是含有多个角度的信息罢了,这就是Self-attention的魔力了。
好了, 下面再看论文里面的描述就非常舒服了,如果令$\mathbf{Q}{k}=\left[\mathbf{Q}{k 1} ; \ldots ; \mathbf{Q}{k h} ; \ldots ; \mathbf{Q}{k H}\right]$, 这里面的$\mathbf{Q}{k h} \in \mathbb{R}^{T \times d{h}}$代表的就是多头里面的某一个头了,由于这多个头合起来的维度$d_{model}$维度,那么一个头就是$d_{h}=\frac{1}{h} d_{\text {model }}$, 这里必须要保证能整除才行。这里用了$h$个头。某个头$h$的计算为: $$ \begin{aligned} \text { head }{h} &=\text { Attention }\left(\mathbf{Q}{k h} \mathbf{W}^{Q}, \mathbf{Q}{k h} \mathbf{W}^{K}, \mathbf{Q}{k h} \mathbf{W}^{V}\right) \ &=\operatorname{softmax}\left(\frac{\mathbf{Q}{k h} \mathbf{W}^{Q} \mathbf{W}^{K^{T}} \mathbf{Q}{k h}^{T}}{\sqrt{d_{m o d e l}}}\right) \mathbf{Q}{k h} \mathbf{W}^{V} \end{aligned} $$ 这里是某一个头的计算过程, 这里的$\mathbf{W}^{Q}, \mathbf{W}^{K}, \mathbf{W}^{Q}$是要学习的参数,由于是一个头,维度应该是$\frac{1}{h} d{\text {model }}\times \frac{1}{h} d_{\text {model }}$, 这样的话softmax那块算出来的是$T \times T$的矩阵, 而后面是一个$T \times \frac{1}{h} d_{\text {model }}$的矩阵,这时候得到的$head_h$是一个$T \times \frac{1}{h} d_{\text {model }}$的矩阵。 而$h$个头的话,正好是$T \times d_{\text {model }}$的维度,也就是我们最后的输出了。即下面这个计算: $$ \mathbf{I}{k}^{Q}=\operatorname{FFN}\left(\text { Concat }\left(\text { head }{1}, \ldots, \text { head }{H}\right) \mathbf{W}^{O}\right) $$ 这个是self-attention 的输出再过一个全连接网络得到的。如果是用残差网络的话,最后的结果依然是个$T \times d{\text {model }}$的,也就是$\mathbf{I}{k}^{Q}$的维度。这时候我们在$T$的维度上进行一个avg pooling的操作,就能够把每个session兴趣转成一个$embedding$维的向量了,即 $$ \mathbf{I}{k}=\operatorname{Avg}\left(\mathbf{I}{k}^{Q}\right) $$ 即这个$\mathbf{I}{k}$是一个embedding维度的向量, 表示当前用户在第$k$会话的兴趣。这就是一个会话里面兴趣提取的全过程了,如果用我之前的神图总结的话就是:
不同点就是这里用了两个transformer块,开始用的是bias编码。
接下来就是不同的会话都走这样的一个Transformer网络,就会得到一个$K \times embed _dim$的矩阵,代表的是某个用户在$K$个会话里面的兴趣信息, 这个就是会话兴趣提取层的结果了。 两个注意点:
- 这$K$个会话是走同一个Transformer网络的,也就是在自注意力机制中不同的会话之间权重共享
- 最后得到的这个矩阵,$K$这个维度上是有时间先后关系的,这为后面用LSTM学习这各个会话之间的兴趣向量奠定了基础。
感觉这篇文章最难的地方在上面这块,所以我用了些篇幅,而下面这些就好说了,因为和之前的东西对上了又。 首先这个会话兴趣交互层
作者这里就是想通过一个双向的LSTM来学习下会话兴趣之间的关系, 从而增加用户兴趣的丰富度,或许还能学习到演化规律。
双向的LSTM这个,这里就不介绍了,关于LSTM之前我也总结过了,无非双向的话,就是先从头到尾计算,在从尾到头回来。所以这里每个时刻隐藏状态的输出计算公式为: $$ \mathbf{H}{t}=\overrightarrow{\mathbf{h}{f t}} \oplus \overleftarrow{\mathbf{h}_{b t}} $$ 这是一个$[1,#hidden_units]$的维度。相加的两项分别是前向传播和反向传播对应的t时刻的hidden state,这里得到的隐藏层状态$H_t$, 我们可以认为是混合了上下文信息的会话兴趣。
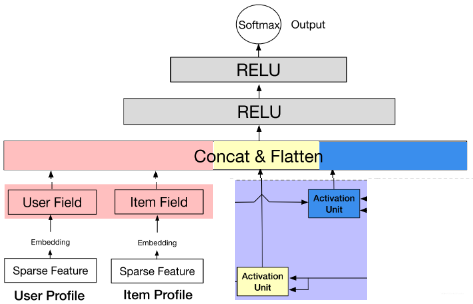
用户的会话兴趣与目标物品越相近,那么应该赋予更大的权重,这里依然使用注意力机制来刻画这种相关性,根据结构图也能看出,这里是用了两波注意力计算:
由于这里的这种局部Attention机制,DIN和DIEN里都见识过了, 这里就不详细解释了, 简单看下公式就可以啦。
- 会话兴趣提取层
$$
\begin{aligned}
a_{k}^{I} &=\frac{\left.\exp \left(\mathbf{I}{k} \mathbf{W}^{I} \mathbf{X}^{I}\right)\right)}{\sum{k}^{K} \exp \left(\mathbf{I}{k} \mathbf{W}^{I} \mathbf{X}^{I}\right)} \
\mathbf{U}^{I} &=\sum{k}^{K} a_{k}^{I} \mathbf{I}_{k}
\end{aligned}
$$
这里$X^I$是候选商品的embedding向量, 是$[embed _dim,1]$的维度,
$I_k$ 是$[1, embed _dim]$的,而$W^I$是一个$[embed _dim, embed _dim]$, 所以这样能算出个分数,表示当前会话兴趣与候选商品之间的相似性程度。 而最终的$U^I$是各个会话兴趣向量的加权线性组合, 维度是$[1, embed _dim]$。 - 会话兴趣交互层
同样,混合了上下文信息的会话兴趣,也进行同样的处理:
$$
\begin{aligned}
a_{k}^{H} &=\frac{\left.\exp \left(\mathbf{H}{k} \mathbf{W}^{H} \mathbf{X}^{I}\right)\right)}{\sum{k}^{K} \exp \left(\mathbf{H}{k} \mathbf{W}^{H} \mathbf{X}^{I}\right)} \
\mathbf{U}^{H} &=\sum{k}^{K} a_{k}^{H} \mathbf{H}_{k}
\end{aligned}
$$
这里$X^I$是候选商品的embedding向量, 是$[embed _dim,1]$的维度,
$H_k$ 是$[1, # hidden _units]$的,而$W^I$是一个$[ # hidden _units, embed _dim]$, 所以这样能算出个分数,当然实际实现,这里都是过神经网络的,表示混合了上下文信息的当前会话兴趣与候选商品之间的相似性程度。 而最终的$U^H$是各个混合了上下文信息的会话兴趣向量的加权线性组合, 维度是$[1, # hidden _units]$。
这个就很简单了,上面的用户行为特征, 物品行为特征以及求出的会话兴趣特征进行拼接,然后过一个DNN网络,就可以得到输出了。
损失这里依然用的交叉熵损失: $$ L=-\frac{1}{N} \sum_{(x, y) \in \mathbb{D}}(y \log p(x)+(1-y) \log (1-p(x))) $$ 这里的$x$表示的是$\left[\mathbf{X}^{U}, \mathbf{X}^{I}, \mathbf{S}\right]$,分布表示用户特征,物品特征和会话兴趣特征。
到这里DSIN模型就解释完毕了。
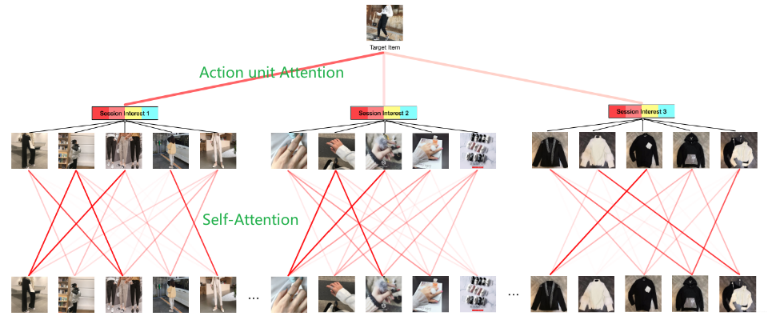
这里的其他细节,后面就是实验部分了,用的数据集是一个广告数据集一个推荐数据集, 对比了几个比较经典的模型Youtubetnet, W&D, DIN, DIEN, 用了RNN的DIN等。并做了一波消融实验,验证了偏置编码的有效性, 会话兴趣抽取层和会话交互兴趣抽取层的有效性。 最后可视化的self-attention和Action Unit的图比较有意思:
好了,下面就是DSIN的代码细节了。
下面就是DSIN的代码部分,这里我依然是借鉴了Deepctr进行的简化版本的复现, 这次复现代码会非常多,因为想借着这个机会学习一波Transformer,具体的还是参考我后面的GitHub。 下面开始:
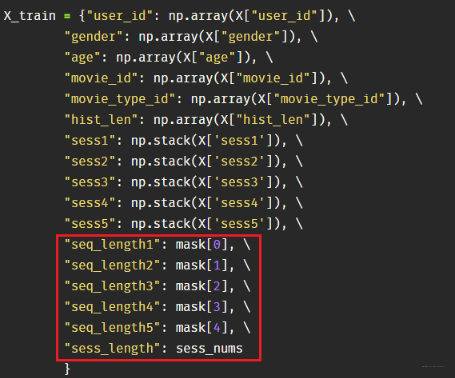
首先, 这里使用的数据集还是movielens数据集,延续的DIEN那里的,没来得及尝试其他,这里说下数据处理部分和DIEN不一样的地方。最大的区别就是这里的用户历史行为上的处理, 之前的是一个历史行为序列列表,这里得需要把这个列表分解成几个会话的形式, 由于每个用户的会话还不一定一样长,所以这里还需要进行填充。具体的数据格式如下:
就是把之前的hist_id序列改成了5个session。其他的特征那里没有变化。 而特征封装那里,需要把这5个会话封装起来,同时还得记录每个用户的有效会话个数以及每个会话里面商品的有效个数, 这个在后面计算里面是有用的,因为目前是padding成了一样长,后面要根据这个个数进行mask, 所以这里有两波mask要做
feature_columns = [SparseFeat('user_id', max(samples_data["user_id"])+1, embedding_dim=8),
SparseFeat('gender', max(samples_data["gender"])+1, embedding_dim=8),
SparseFeat('age', max(samples_data["age"])+1, embedding_dim=8),
SparseFeat('movie_id', max(samples_data["movie_id"])+1, embedding_dim=8),
SparseFeat('movie_type_id', max(samples_data["movie_type_id"])+1, embedding_dim=8),
DenseFeat('hist_len', 1)]
feature_columns += [VarLenSparseFeat('sess1', vocabulary_size=max(samples_data["movie_id"])+1, embedding_dim=8, maxlen=10, length_name='seq_length1'),
VarLenSparseFeat('sess2', vocabulary_size=max(samples_data["movie_id"])+1, embedding_dim=8, maxlen=10, length_name='seq_length2'),
VarLenSparseFeat('sess3', vocabulary_size=max(samples_data["movie_id"])+1, embedding_dim=8, maxlen=10, length_name='seq_length3'),
VarLenSparseFeat('sess4', vocabulary_size=max(samples_data["movie_id"])+1, embedding_dim=8, maxlen=10, length_name='seq_length4'),
VarLenSparseFeat('sess5', vocabulary_size=max(samples_data["movie_id"])+1, embedding_dim=8, maxlen=10, length_name='seq_length5'),
]
feature_columns += ['sess_length']封装代码变成了上面这个样子, 之所以放这里, 我是想说明一个问题,也是我这次才刚刚发觉的,就是这块封装特征的代码是用于建立模型用的, 也就是不用管有没有数据集,只要基于这个feature_columns就能把模型建立出来。 而这里面有几个重要的细节要梳理下:
- 上面的那一块特征是常规的离散和连续特征,封装起来即可,这个会对应的建立Input层接收后面的数据输入
- 第二块的变长离散特征, 注意后面的
seq_length,这个东西的作用是标记每个用户在每个会话里面有效商品的真实长度,所以这5个会话建Input层的时候,不仅给前面的sess建立Input,还会给length_name建立Input层来接收每个用户每个会话里面商品的真实长度信息, 这样在后面创建mask的时候才有效。也就是没有具体数据之前网络就能创建mask信息才行。这个我是遇到了坑的,之前又忽略了这个seq_length, 想着直接用上面的真实数据算出长度来给网络不就行? 其实不行,因为我们算出来的长度mask给网络的时候,那个样本数已经确定了,这时候会出bug的到后面。 因为真实训练的时候,batch_size是我们自己指定。并且这个思路的话是网络依赖于数据才能建立出来,显然是不合理的。所以一定要切记,先用seq_length在这里占坑,作为一个Input层, 然后过embedding,后面基于传进的序列长度和填充的最大长度用tf.sequence_mask就能建立了。 - 最后的
sess_length, 这个标记每个用户的有效会话个数,后面在会话兴趣与当前候选商品算注意力的时候,也得进行mask操作,所以这里和上面这个原理是一样的,必须先用sess_length在这里占坑,创建一个Input层。 - 对应关系, 既然我们这里封装的时候是这样封装的,这样就会根据上面的建立出不同的Input层,这时候我们具体用X训练的时候,一定要注意数据对应,也就是特征必须够且能对应起来,这里是通过名字对应的, 看下面的X:
真实数据要和Input层接收进行对应好。
好了,关于数据处理就说这几个细节,感觉mask的那个处理非常需要注意。具体的看代码就可以啦。下面重头戏,剖析模型。
有了Deepctr的这种代码风格,使得建立模型会从宏观上看起来非常清晰,简单说下逻辑, 先建立输入层,由于输入的特征有三大类(离散,连续和变长离散),所以分别建立Input层,然后离散特征还得建立embedding层。下面三大类特征就有了不同的走向:
- 连续特征: 这类特征拼先拼接到一块,然后等待最后往DNN里面输入
- 普通离散特征: 这块从输入 -> embedding -> 拼接到一块,等待DNN里面输入
- 用户的会话特征: 这块从输入 -> embedding -> 会话兴趣分割层(
sess_interest_division) -> 会话兴趣提取层(sess_interest_extractor) -> 会话兴趣交互层(BiLSTM) -> 会话兴趣激活层(AttentionPoolingLayer) -> 得到两个兴趣性特征
把上面的连续特征,离散特征和兴趣特征拼接起来,然后过DNN得到输出即可。就是这么个逻辑了,具体代码如下:
def DSIN(feature_columns, sess_feature_list, sess_max_count=5, bias_encoding=True, singlehead_emb_size=1,
att_head_nums=8, dnn_hidden_units=(200, 80)):
"""
建立DSIN网络
:param feature_columns: A list, 每个特征的封装 nametuple形式
:param behavior_feature_list: A list, 行为特征名称
:param sess_max_count: 会话的个数
:param bias_encoding: 是否偏置编码
:singlehead_emb_size: 每个头的注意力的维度,注意这个和头数的乘积必须等于输入的embedding的维度
:att_head_nums: 头的个数
:dnn_hidden_units: 这个是全连接网络的神经元个数
"""
# 检查下embedding设置的是否合法,因为这里有了多头注意力机制之后,我们要保证我们的embedding维度 = att_head_nums * att_embedding_size
hist_emb_size = sum(
map(lambda fc: fc.embedding_dim, filter(lambda fc: fc.name in sess_feature_list, [feature for feature in feature_columns if not isinstance(feature, str)]))
)
if singlehead_emb_size * att_head_nums != hist_emb_size:
raise ValueError(
"hist_emb_size must equal to singlehead_emb_size * att_head_nums ,got %d != %d *%d" % (
hist_emb_size, singlehead_emb_size, att_head_nums))
# 建立输入层
input_layer_dict = build_input_layers(feature_columns)
# 将Input层转化为列表的形式作为model的输入
input_layers = list(input_layer_dict.values()) # 各个输入层
input_keys = list(input_layer_dict.keys()) # 各个列名
user_sess_seq_len = [input_layer_dict['seq_length'+str(i+1)] for i in range(sess_max_count)]
user_sess_len = input_layer_dict['sess_length']
# 筛选出特征中的sparse_fra, dense_fea, varlen_fea
sparse_feature_columns = list(filter(lambda x: isinstance(x, SparseFeat), feature_columns)) if feature_columns else []
dense_feature_columns = list(filter(lambda x: isinstance(x, DenseFeat), feature_columns)) if feature_columns else []
varlen_sparse_feature_columns = list(filter(lambda x: isinstance(x, VarLenSparseFeat), feature_columns)) if feature_columns else []
# 获取dense
dnn_dense_input = []
for fc in dense_feature_columns:
dnn_dense_input.append(input_layer_dict[fc.name])
# 将所有的dense特征拼接
dnn_dense_input = concat_input_list(dnn_dense_input)
# 构建embedding词典
embedding_layer_dict = build_embedding_layers(feature_columns, input_layer_dict)
# 因为这里最终需要将embedding拼接后直接输入到全连接层(Dense)中, 所以需要Flatten
dnn_sparse_embed_input = concat_embedding_list(sparse_feature_columns, input_layer_dict, embedding_layer_dict, flatten=True)
# 将所有sparse特征的embedding进行拼接
dnn_sparse_input = concat_input_list(dnn_sparse_embed_input)
# dnn_dense_input和dnn_sparse_input这样就不用管了,等待后面的拼接就完事, 下面主要是会话行为兴趣的提取
# 首先获取当前的行为特征(movie)的embedding,这里有可能有多个行为产生了行为序列,所以需要使用列表将其放在一起
# 这个东西最后求局域Attention的时候使用,也就是选择与当前候选物品最相关的会话兴趣
query_embed_list = embedding_lookup(sess_feature_list, input_layer_dict, embedding_layer_dict)
query_emb = concat_input_list(query_embed_list)
# 下面就是开始会话行为的处理了,四个层来: 会话分割层,会话兴趣提取层,会话兴趣交互层和局部Attention层,下面一一来做
# 首先这里是找到会话行为中的特征列的输入层, 其实用input_layer_dict也行
user_behavior_input_dict = {}
for idx in range(sess_max_count):
sess_input = OrderedDict()
for i, feat in enumerate(sess_feature_list): # 我这里只有一个movie_id
sess_input[feat] = input_layer_dict["sess" + str(idx+1)]
user_behavior_input_dict['sess'+str(idx+1)] = sess_input # 这里其实是获取那五个会话的输入层
# 会话兴趣分割层: 拿到每个会话里面各个商品的embedding,并且进行偏置编码,得到transformer的输入
transformer_input = sess_interest_division(embedding_layer_dict, user_behavior_input_dict,
sparse_feature_columns, sess_feature_list,
sess_max_count, bias_encoding=bias_encoding)
# 这个transformer_input是个列表,里面的每个元素代表一个会话,维度是(None, max_seq_len, embed_dim)
# 会话兴趣提取层: 每个会话过transformer,从多个角度得到里面各个商品之间的相关性(交互)
self_attention = Transformer(singlehead_emb_size, att_head_nums, dropout_rate=0, use_layer_norm=True,
use_positional_encoding=(not bias_encoding), blinding=False)
sess_fea = sess_interest_extractor(transformer_input, sess_max_count, self_attention, user_sess_seq_len)
# 这里的输出sess_fea是个矩阵,维度(None, sess_max_cout, embed_dim), 这个东西后期要和当前的候选商品求Attention进行sess维度上的加权
# 会话兴趣交互层 上面的transformer结果,过双向的LSTM
lstm_output = BiLSTM(hist_emb_size, layers=2, res_layers=0, dropout_rate=0.2)(sess_fea)
# 这个lstm_output是个矩阵,维度是(None, sess_max_count, hidden_units_num)
# 会话兴趣激活层 这里就是计算两波注意力
interest_attention = AttentionPoolingLayer(user_sess_len)([query_emb, sess_fea])
lstm_attention = AttentionPoolingLayer(user_sess_len)([query_emb, lstm_output])
# 上面这两个的维度分别是(None, embed_size), (None, hidden_units_num) 这里embed_size=hidden_units_num
# 下面就是把dnn_sense_input, dnn_sparse_input, interest_attention, lstm_attention拼接起来
deep_input = Concatenate(axis=-1)([dnn_dense_input, dnn_sparse_input, interest_attention, lstm_attention])
# 全连接接网络, 获取最终的dnn_logits
dnn_logits = get_dnn_logits(deep_input, activation='prelu')
model = Model(input_layers, dnn_logits)
# 所有变量需要初始化
tf.compat.v1.keras.backend.get_session().run(tf.compat.v1.global_variables_initializer())
return model下面开始解释每块的细节实现。
这里面接收的输入是一个每个用户的会话列表, 比如上面那5个会话的时候,每个会话里面是有若干个商品的,当然还不仅仅是有商品id,还有可能有类别id这种。 而这个函数干的事情就是遍历这5个会话,然后对于每个会话,要根据商品id拿到每个会话的商品embedding(有类别id的话也会拿到类别id然后拼起来), 所以每个会话会得到一个(None, seq_len, embed_dim)的一个矩阵,而最后的输出就是5个会话的矩阵放到一个列表里返回来。也就是上面的transformer_input, 作为transformer的输入。 这里面的一个细节,就是偏置编码。 如果需要偏置编码的话,要在这里面进行。偏置编码的过程
class BiasEncoding(Layer):
"""位置编码"""
def __init__(self, sess_max_count, seed=1024):
super(BiasEncoding, self).__init__()
self.sess_max_count = sess_max_count
self.seed = seed
def build(self, input_shape):
# 在该层创建一个可训练的权重 input_shape [None, sess_max_count, max_seq_len, embed_dim]
if self.sess_max_count == 1:
embed_size = input_shape[2]
seq_len_max = input_shape[1]
else:
embed_size = input_shape[0][2]
seq_len_max = input_shape[0][1]
# 声明那三个位置偏置编码矩阵
self.sess_bias_embedding = self.add_weight('sess_bias_encoding', shape=(self.sess_max_count, 1, 1),
initializer=tf.keras.initializers.TruncatedNormal(mean=0.0, stddev=0.0001, seed=self.seed)) # 截断产生正太随机数
self.seq_bias_embedding = self.add_weight('seq_bias_encoding', shape=(1, seq_len_max, 1),
initializer=tf.keras.initializers.TruncatedNormal(mean=0.0, stddev=0.0001, seed=self.seed))
self.embed_bias_embedding = self.add_weight('embed_beas_encoding', shape=(1, 1, embed_size),
initializer=tf.keras.initializers.TruncatedNormal(mean=0.0, stddev=0.0001, seed=self.seed))
super(BiasEncoding, self).build(input_shape)
def call(self, inputs, mask=None):
"""
:param inputs: A list 长度是会话数量,每个元素表示一个会话矩阵,维度是[None, max_seq_len, embed_dim]
"""
bias_encoding_out = []
for i in range(self.sess_max_count):
bias_encoding_out.append(
inputs[i] + self.embed_bias_embedding + self.seq_bias_embedding + self.sess_bias_embedding[i] # 这里会广播
)
return bias_encoding_out 这里的核心就是build里面的那三个偏置矩阵,对应论文里面的$\mathbf{w}{k}^{K},\mathbf{w}{t}^{T},\mathbf{w}_{c}^{C}$, 这里之所以放到build里面建立,是为了让这些参数可学习, 而前向传播里面就是论文里面的公式加就完事,这里面会用到广播机制。
这里面就是复现了大名鼎鼎的Transformer了, 这也是我第一次看transformer的代码,果真与之前的理论分析还是有很多不一样的点,下面得一一梳理一下,Transformer是非常重要的。
首先是位置编码, 代码如下:
def positional_encoding(inputs, pos_embedding_trainable=True,scale=True):
"""
inputs: (None, max_seq_len, embed_dim)
"""
_, T, num_units = inputs.get_shape().as_list() # [None, max_seq_len, embed_dim]
position_ind = tf.expand_dims(tf.range(T), 0) # [1, max_seq_len]
# First part of the PE function: sin and cos argument
position_enc = np.array([
[pos / np.power(1000, 2. * i / num_units) for i in range(num_units)] for pos in range(T)
])
# Second part, apply the cosine to even columns and sin to odds. # 这个操作秀
position_enc[:, 0::2] = np.sin(position_enc[:, 0::2]) # dim 2i
position_enc[:, 1::2] = np.cos(position_enc[:, 1::2]) # dim 2i+1
# 转成张量
if pos_embedding_trainable:
lookup_table = K.variable(position_enc, dtype=tf.float32)
outputs = tf.nn.embedding_lookup(lookup_table, position_ind)
if scale:
outputs = outputs * num_units ** 0.5
return outputs + inputs这一块的话没有啥好说的东西感觉,这个就是在按照论文里面的公式sin, cos变换, 这里面比较秀的操作感觉就是dim2i和dim 2i+1的赋值了。
接下来,LayerNormalization, 这个也是按照论文里面的公式实现的代码,求均值和方差的维度都是embedding:
class LayerNormalization(Layer):
def __init__(self, axis=-1, eps=1e-9, center=True, scale=True):
super(LayerNormalization, self).__init__()
self.axis = axis
self.eps = eps
self.center = center
self.scale = scale
def build(self, input_shape):
"""
input_shape: [None, max_seq_len, singlehead_emb_dim*head_num]
"""
self.gamma = self.add_weight(name='gamma', shape=input_shape[-1:], # [1, max_seq_len, singlehead_emb_dim*head_num]
initializer=tf.keras.initializers.Ones(), trainable=True)
self.beta = self.add_weight(name='beta', shape=input_shape[-1:],
initializer=tf.keras.initializers.Zeros(), trainable=True) # [1, max_seq_len, singlehead_emb_dim*head_num]
super(LayerNormalization, self).build(input_shape)
def call(self, inputs):
"""
[None, max_seq_len, singlehead_emb_dim*head_num]
"""
mean = K.mean(inputs, axis=self.axis, keepdims=True) # embed_dim维度上求均值
variance = K.mean(K.square(inputs-mean), axis=-1, keepdims=True) # embed_dim维度求方差
std = K.sqrt(variance + self.eps)
outputs = (inputs - mean) / std
if self.scale:
outputs *= self.gamma
if self.center:
outputs += self.beta
return outputs 下面就是伟大的Transformer网络,下面我先把整体代码放上来,然后解释一些和我之前见到过的一样的地方,也是通过看具体代码学习到的点:
class Transformer(Layer):
"""Transformer网络"""
def __init__(self, singlehead_emb_size=1, att_head_nums=8, dropout_rate=0.0, use_positional_encoding=False,use_res=True,
use_feed_forword=True, use_layer_norm=False, blinding=False, seed=1024):
super(Transformer, self).__init__()
self.singlehead_emb_size = singlehead_emb_size
self.att_head_nums = att_head_nums
self.num_units = self.singlehead_emb_size * self.att_head_nums
self.use_res = use_res
self.use_feed_forword = use_feed_forword
self.dropout_rate = dropout_rate
self.use_positional_encoding = use_positional_encoding
self.use_layer_norm = use_layer_norm
self.blinding = blinding # 如果为True的话表明进行attention的时候未来的units都被屏蔽, 解码器的时候用
self.seed = seed
# 这里需要为该层自定义可训练的参数矩阵 WQ, WK, WV
def build(self, input_shape):
# input_shape: [None, max_seq_len, embed_dim]
embedding_size= int(input_shape[0][-1])
# 检查合法性
if self.num_units != embedding_size:
raise ValueError(
"att_embedding_size * head_num must equal the last dimension size of inputs,got %d * %d != %d" % (
self.singlehead_emb_size, att_head_nums, embedding_size))
self.seq_len_max = int(input_shape[0][-2])
# 定义三个矩阵
self.W_Query = self.add_weight(name='query', shape=[embedding_size, self.singlehead_emb_size*self.att_head_nums],
dtype=tf.float32,initializer=tf.keras.initializers.TruncatedNormal(seed=self.seed))
self.W_Key = self.add_weight(name='key', shape=[embedding_size, self.singlehead_emb_size*self.att_head_nums],
dtype=tf.float32,initializer=tf.keras.initializers.TruncatedNormal(seed=self.seed+1))
self.W_Value = self.add_weight(name='value', shape=[embedding_size, self.singlehead_emb_size*self.att_head_nums],
dtype=tf.float32,initializer=tf.keras.initializers.TruncatedNormal(seed=self.seed+2))
# 用神经网络的话,加两层训练参数
if self.use_feed_forword:
self.fw1 = self.add_weight('fw1', shape=[self.num_units, 4 * self.num_units], dtype=tf.float32,
initializer=tf.keras.initializers.glorot_uniform(seed=self.seed))
self.fw2 = self.add_weight('fw2', shape=[4 * self.num_units, self.num_units], dtype=tf.float32,
initializer=tf.keras.initializers.glorot_uniform(seed=self.seed+1))
self.dropout = tf.keras.layers.Dropout(self.dropout_rate)
self.ln = LayerNormalization()
super(Transformer, self).build(input_shape)
def call(self, inputs, mask=None, training=None):
"""
:param inputs: [当前会话sessi, 当前会话sessi] 维度 (None, max_seq_len, embed_dim)
:param mask: 当前会话mask 这是个1维数组, 维度是(None, ), 表示每个样本在当前会话里面的行为序列长度
"""
# q和k其实是一样的矩阵
queries, keys = inputs
query_masks, key_masks = mask, mask
# 这里需要对Q和K进行mask操作,
# key masking目的是让key值的unit为0的key对应的attention score极小,这样加权计算value时相当于对结果不产生影响
# Query Masking 要屏蔽的是被0所填充的内容。
query_masks = tf.sequence_mask(query_masks, self.seq_len_max, dtype=tf.float32) # (None, 1, seq_len_max)
key_masks = tf.sequence_mask(key_masks, self.seq_len_max, dtype=tf.float32) # (None, 1, seq_len_max), 注意key_masks开始是(None,1)
key_masks = key_masks[:, 0, :] # 所以上面会多出个1维度来, 这里去掉才行,(None, seq_len_max)
query_masks = query_masks[:, 0, :] # 这个同理
# 是否位置编码
if self.use_positional_encoding:
queries = positional_encoding(queries)
keys = positional_encoding(queries)
# tensordot 是矩阵乘,好处是当两个矩阵维度不同的时候,只要指定axes也可以乘
# 这里表示的是queries的-1维度与W_Query的0维度相乘
# (None, max_seq_len, embedding_size) * [embedding_size, singlehead_emb_size*head_num]
querys = tf.tensordot(queries, self.W_Query, axes=(-1, 0)) # [None, max_seq_len_q, singlehead_emb_size*head_num]
keys = tf.tensordot(keys, self.W_Key, axes=(-1, 0)) # [None, max_seq_len_k, singlehead_emb_size*head_num]
values = tf.tensordot(keys, self.W_Value, axes=(-1, 0)) # [None, max_seq_len_k, singlehead_emb_size*head_num]
# tf.split切分张量 这里从头那里切分成head_num个张量, 然后从0维拼接
querys = tf.concat(tf.split(querys, self.att_head_nums, axis=2), axis=0) # [head_num*None, max_seq_len_q, singlehead_emb_size]
keys = tf.concat(tf.split(keys, self.att_head_nums, axis=2), axis=0) # [head_num*None, max_seq_len_k, singlehead_emb_size]
values = tf.concat(tf.split(values, self.att_head_nums, axis=2), axis=0) # [head_num*None, max_seq_len_k, singlehead_emb_size]
# Q*K keys后两维转置然后再乘 [head_num*None, max_seq_len_q, max_seq_len_k]
outputs = tf.matmul(querys, keys, transpose_b=True)
outputs = outputs / (keys.get_shape().as_list()[-1] ** 0.5)
# 从0维度上复制head_num次
key_masks = tf.tile(key_masks, [self.att_head_nums, 1]) # [head_num*None, max_seq_len_k]
key_masks = tf.tile(tf.expand_dims(key_masks, 1), [1, tf.shape(queries)[1], 1]) # [head_num*None, max_seq_len_q,max_seq_len_k]
paddings = tf.ones_like(outputs) * (-2**32+1)
outputs = tf.where(tf.equal(key_masks, 1), outputs, paddings) # 被填充的部分赋予极小的权重
# 标识是否屏蔽未来序列的信息(解码器self attention的时候不能看到自己之后的哪些信息)
# 这里通过下三角矩阵的方式进行,依此表示预测第一个词,第二个词,第三个词...
if self.blinding:
diag_vals = tf.ones_like(outputs[0, :, :]) # (T_q, T_k)
tril = tf.linalg.LinearOperatorLowerTriangular(diag_vals).to_dense() # (T_q, T_k) 这是个下三角矩阵
masks = tf.tile(tf.expand_dims(tril, 0), [tf.shape(outputs)[0], 1, 1]) # (h*N, T_q, T_k)
paddings = tf.ones_like(masks) * (-2 ** 32 + 1)
outputs = tf.where(tf.equal(masks, 0), paddings, outputs) # (h*N, T_q, T_k)
outputs -= tf.reduce_max(outputs, axis=-1, keepdims=True)
outputs = tf.nn.softmax(outputs, axis=-1) # 最后一个维度求softmax,换成权重
query_masks = tf.tile(query_masks, [self.att_head_nums, 1]) # [head_num*None, max_seq_len_q]
query_masks = tf.tile(tf.expand_dims(query_masks, -1), [1, 1, tf.shape(keys)[1]]) # [head_num*None, max_seq_len_q, max_seq_len_k]
outputs *= query_masks
# 权重矩阵过下dropout [head_num*None, max_seq_len_q, max_seq_len_k]
outputs = self.dropout(outputs, training=training)
# weighted sum [head_num*None, max_seq_len_q, max_seq_len_k] * # [head_num*None, max_seq_len_k, singlehead_emb_size]
result = tf.matmul(outputs, values) # [head_num*None, max_seq_len_q, singlehead_emb_size]
# 换回去了
result = tf.concat(tf.split(result, self.att_head_nums, axis=0), axis=2) # [None, max_seq_len_q, head_num*singlehead_emb_size]
if self.use_res: # 残差连接
result += queries
if self.use_layer_norm:
result = self.ln(result)
if self.use_feed_forword: # [None, max_seq_len_q, head_num*singlehead_emb_size] 与 [num_units, self.num_units]
fw1 = tf.nn.relu(tf.tensordot(result, self.fw1, axes=[-1, 0])) # [None, max_seq_len_q, 4*num_units]
fw1 = self.dropout(fw1, training=training)
fw2 = tf.tensordot(fw1, self.fw2, axes=[-1, 0]) # [None, max_seq_len_q, num_units] 这个num_units其实就等于head_num*singlehead_emb_size
if self.use_res:
result += fw2
if self.use_layer_norm:
result = self.ln(result)
return tf.reduce_mean(result, axis=1, keepdims=True) # [None, 1, head_num*singleh]这里面的整体逻辑, 首先在build里面会构建3个矩阵WQ, WK, WV,在这里定义依然是为了这些参数可训练, 而出乎我意料的是残差网络的参数w也是这里定义, 之前还以为这个是单独写出来,后面看了前向传播的逻辑时候明白了。
前向传播的逻辑和我之前画的图上差不多,不一样的细节是这里的具体实现上, 就是这里的把多个头分开,采用堆叠的方式进行计算(堆叠到第一个维度上去了)。这个是我之前忽略的一个问题, 只有这样才能使得每个头与每个头之间的自注意力运算是独立不影响的。如果不这么做的话,最后得到的结果会含有当前单词在这个头和另一个单词在另一个头上的关联,这是不合理的。这是看了源码之后才发现的细节。
另外就是mask操作这里,Q和K都需要进行mask操作,因为我们接受的输入序列是经过填充的,这里必须通过指明长度在具体计算的时候进行遮盖,否则softmax那里算的时候会有影响,因为e的0次方是1,所以这里需要找到序列里面填充的那些地方,给他一个超级大的负数,这样e的负无穷接近0,才能没有影响。但之前不知道这里的细节,这次看发现是Q和K都进行mask操作,且目的还不一样。
第三个细节,就是对未来序列的屏蔽,这个在这里是用不到的,这个是Transformer的解码器用的一个操作,就是在解码的时候,我们不能让当前的序列看到自己之后的信息。这里也需要进行mask遮盖住后面的。而具体实现,竟然使用了一个下三角矩阵, 这个东西的感觉是这样:
解码的时候,只能看到自己及以前的相关性,然后加权,这个学到了哈哈。
transformer这里接收的是会话兴趣分割层传下来的兴趣列表,返回的是个矩阵,维度是(None, sess_nums, embed_dim), 因为这里每个会话都要过Transformer, 输入的维度是(None, seq_len, embed_dim), 而经过transformer之后,本来输出的维度也是这个,但是最后返回的时候在seq_len的维度上求了个平均。所以每个会话得到的输出是(None, 1, embed_dim), 相当于兴趣综合了下。而5个会话,就会得到5个这样的结果,然后再会话维度上拼接,就是上面的这个矩阵结果了,这个东西作为双向LSTM的输入。
这里主要是值得记录下多层双向LSTM的实现过程, 用下面的这种方式非常的灵活:
class BiLSTM(Layer):
def __init__(self, units, layers=2, res_layers=0, dropout_rate=0.2, merge_mode='ave'):
super(BiLSTM, self).__init__()
self.units = units
self.layers = layers
self.res_layers = res_layers
self.dropout_rate = dropout_rate
self.merge_mode = merge_mode
# 这里要构建正向的LSTM和反向的LSTM, 因为我们是要两者的计算结果最后加和,所以这里需要分别计算
def build(self, input_shape):
"""
input_shape: (None, sess_max_count, embed_dim)
"""
self.fw_lstm = []
self.bw_lstm = []
for _ in range(self.layers):
self.fw_lstm.append(
LSTM(self.units, dropout=self.dropout_rate, bias_initializer='ones', return_sequences=True, unroll=True)
)
# go_backwards 如果为真,则反向处理输入序列并返回相反的序列
# unroll 布尔(默认错误)。如果为真,则网络将展开,否则使用符号循环。展开可以提高RNN的速度,尽管它往往会占用更多的内存。展开只适用于较短的序列。
self.bw_lstm.append(
LSTM(self.units, dropout=self.dropout_rate, bias_initializer='ones', return_sequences=True, go_backwards=True, unroll=True)
)
super(BiLSTM, self).build(input_shape)
def call(self, inputs):
input_fw = inputs
input_bw = inputs
for i in range(self.layers):
output_fw = self.fw_lstm[i](input_fw)
output_bw = self.bw_lstm[i](input_bw)
output_bw = Lambda(lambda x: K.reverse(x, 1), mask=lambda inputs, mask:mask)(output_bw)
if i >= self.layers - self.res_layers:
output_fw += input_fw
output_bw += input_bw
input_fw = output_fw
input_bw = output_bw
if self.merge_mode == "fw":
output = output_fw
elif self.merge_mode == "bw":
output = output_bw
elif self.merge_mode == 'concat':
output = K.concatenate([output_fw, output_bw])
elif self.merge_mode == 'sum':
output = output_fw + output_bw
elif self.merge_mode == 'ave':
output = (output_fw + output_bw) / 2
elif self.merge_mode == 'mul':
output = output_fw * output_bw
elif self.merge_mode is None:
output = [output_fw, output_bw]
return output这里这个操作是比较骚的,以后建立双向LSTM就用这个模板了,具体也不用解释,并且这里之所以说灵活,是因为最后前向LSTM的结果和反向LSTM的结果都能单独的拿到,且可以任意的两者运算。 我记得Keras里面应该是也有直接的函数实现双向LSTM的,但依然感觉不如这种灵活。 这个层数自己定,单元自己定看,最后结果形式自己定,太帅了简直。 关于LSTM,可以看官方文档
这个的输入是(None, sess_nums, embed_dim), 输出是(None, sess_nums, hidden_units_num)。
这里就是局部Attention的操作了,这个在这里就不解释了,和之前的DIEN,DIN的操作就一样了, 代码也不放在这里了,剩下的代码都看后面的GitHub链接吧, 这里我只记录下我觉得后面做别的项目会有用的代码哈哈。
DSIN的核心创新点就是把用户的历史行为按照时间间隔进行切分,以会话为单位进行学习, 而学习的方式首先是会话之内的行为自学习,然后是会话之间的交互学习,最后是与当前候选商品相关的兴趣演进,总体上还是挺清晰的。
具体的实际使用场景依然是有丰富的用户历史行为序列才可以,而会话之间的划分间隔,也得依据具体业务场景。 具体的使用可以调deepctr的包。
参考资料: