Skip to content

ODE_LotkaVolterra

Jump to bottom
Julius Bañgate edited this page Apr 16, 2023 · 3 revisions
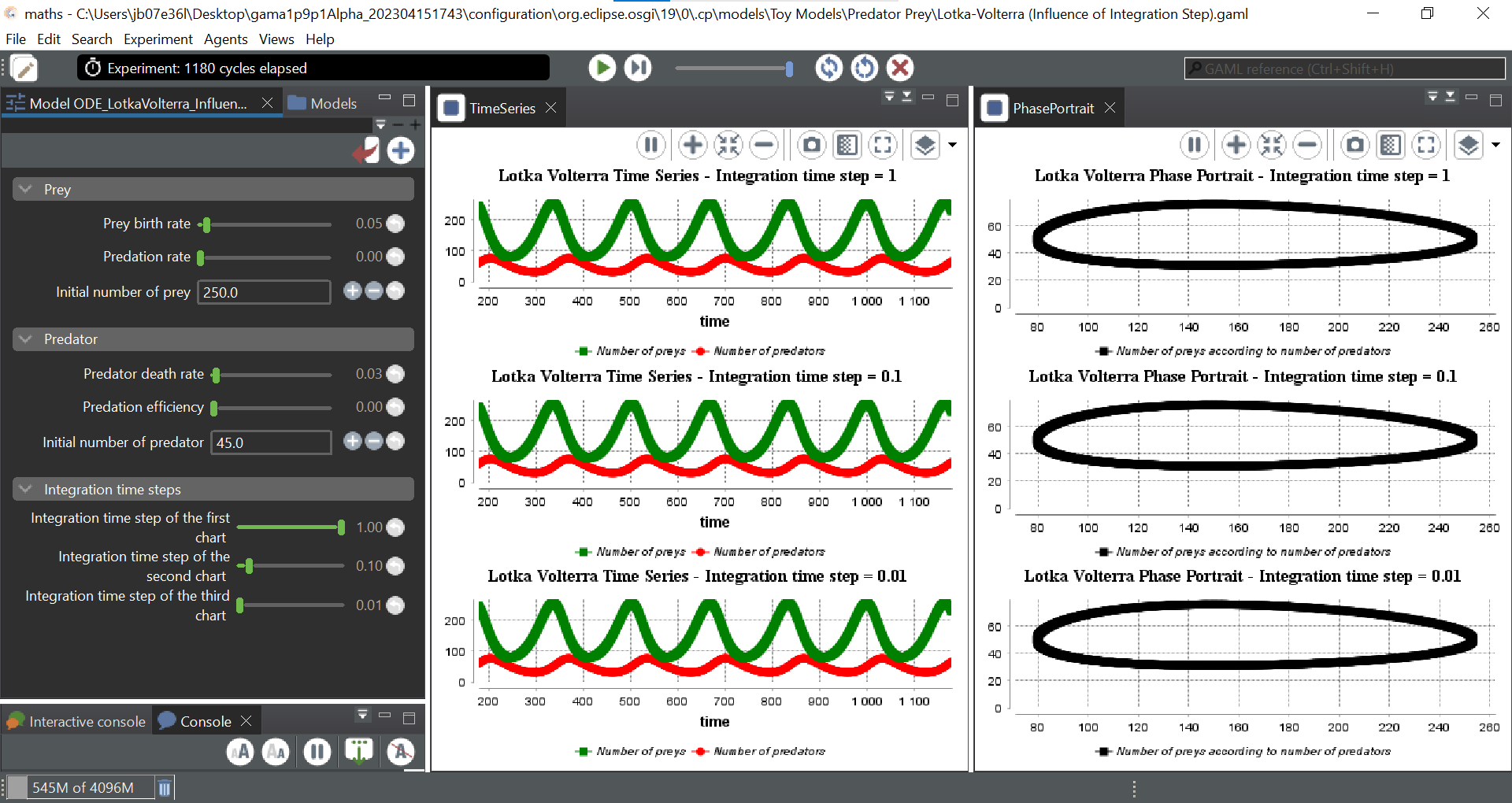
Annotation 2023-04-16 043606_LotkaVolterraInfInteg

Path: Library models/Toy Models/Predator Prey/Lotka-Volterra (Influence of Integration Step).gaml

/**
* Name: ODE_LotkaVolterra
* Author: Huynh Quang Nghi & Nathalie Corson
*  Description: Lotka Volterra Predator Prey Model - ODE solved with Runge-Kutta 4 method with different integration time step
* Tags: equation, math
*/

model ODE_LotkaVolterra_InfluenceTimeStep

global {

	float prey_birth_rate ; 		// natural birth rate of preys
	float predation_rate ; 			// death rate of preys due to predators
	float predator_death_rate ; 	// natural death rate of predators
	float predation_efficiency ; 	// birth rate of predators due to prey consumption
	
	float nb_prey_init ; 			// initial number of preys
	float nb_predator_init  ; 		// initial number of predators
	
	float integration_step ; 	// integration time step of the Runge Kutta 4 method
	float t;   					// simulation time : t = n * integration_time_step  where n is the number of already computed time step
	
	
	float integration_time_step1  <- 1.0;  // first integration time step to compare 
	float integration_time_step2  <- 0.1;  // second integration time step to compare 
	float integration_time_step3  <- 0.01;  // third integration time step to compare 
	
	list<LotkaVolterra_agent> LV_agents;
	
	init{
		create LotkaVolterra_agent number: 1 with:[integration_time_step::integration_time_step1]; 	// creation of an agent containing the ODE model with an integration time step of value integration_time_step1
		create LotkaVolterra_agent number: 1 with:[integration_time_step::integration_time_step2]; 	// creation of an agent containing the ODE model with an integration time step of value integration_time_step2
		create LotkaVolterra_agent number: 1 with:[integration_time_step::integration_time_step3]; 	// creation of an agent containing the ODE model with an integration time step of value integration_time_step3
		LV_agents <- list(LotkaVolterra_agent);
	}
}

species LotkaVolterra_agent {
	
    float nb_prey <- nb_prey_init ; 				// number of preys initialized with the values given by the user
	float nb_predator <- nb_predator_init ; 		// number of predators initialized with the values given by the user
	
	float integration_time_step ; 					// integration time step used in the Runge Kutta 4 method
  
	equation lotka_volterra { 
		diff(nb_prey,t) =   nb_prey * (prey_birth_rate - predation_rate * nb_predator); 					// evolution of the number of preys duting an integration time step
		diff(nb_predator,t) = - nb_predator * (predator_death_rate - predation_efficiency * nb_prey); 		// evolution of the number of predator during an integration time step
      }
      reflex solving {        
       	solve lotka_volterra method: "rk4" step_size:integration_time_step;									// use of runge kutta 4 method with an integration time step of value integration_time_step
       }
}


experiment maths type: gui {
		
	parameter "Prey birth rate" var: prey_birth_rate <- 0.05 min: 0.0 max: 1.0 category: "Prey";						// the user defines the value of parameter prey_birth_rate on the interface, the default value is 0.05 and this value must be between 0 and 1
	parameter "Predation rate" var: predation_rate <- 0.001 min: 0.0 max: 1.0 category: "Prey"; 						// the user defines the value of parameter prey_birth_rate on the interface, the default value is 0.001 and this value must be between 0 and 1
	parameter "Predator death rate" var: predator_death_rate <- 0.03 min: 0.0 max: 1.0 category: "Predator";	 		// the user defines the value of parameter predator_death_rate on the interface, the default value is 0.03 and this value must be between 0 and 1
	parameter "Predation efficiency" var: predation_efficiency <- 0.0002 min: 0.0 max: 1.0 category: "Predator";		// the user defines the value of parameter predation_efficiency on the interface, the default value is 0.0002 and this value must be between 0 and 1
	
	parameter "Initial number of prey" var: nb_prey_init <- 250.0 min: 1.0 category: "Prey"; 							// the user defines the value of parameter predation_efficiency on the interface, the default value is 250, the minimum possible value is 1
	parameter "Initial number of predator" var: nb_predator_init <- 45.0 min: 1.0 category: "Predator"; 				// the user defines the value of parameter predation_efficiency on the interface, the default value is 45, the minimum possible value is 1
	
	parameter "Integration time step of the first chart " var:  integration_time_step1 <- 1.0  min: 0.0 max:1.0 category: "Integration time steps"; 	// the user defines the value of the first integration step he wants to compare, the default value is 1 and this value must be between 0 and 1
	parameter "Integration time step of the second chart " var:  integration_time_step2 <- 0.1  min: 0.0 max: 1.0 category: "Integration time steps"; 	// the user defines the value of the second integration step he wants to compare, the default value is 0.1 and this value must be between 0 and 1
	parameter "Integration time step of the third chart " var:  integration_time_step3 <- 0.01  min: 0.0 max: 1.0 category: "Integration time steps"; 	// the user defines the value of the third integration step he wants to compare, the default value is 0.01 and this value must be between 0 and 1
		
	output {		
 		display TimeSeries  type: 2d  {	// creation of a display to show time series of the model, values are plotted at every step. Since there is more than one chart plotted in one display, every chart has a position and a size
			chart "Lotka Volterra Time Series - Integration time step = 1 " type: series background: #white position: {0,0} size:{1,0.33} x_range: 1000 { 		// one chart, of type 'serie', is named Lotka Volterra Time Series - Integration time step = 1, it shows quantities according to time, and the background is white
				data 'Number of preys' value: first(LotkaVolterra_agent where (each.integration_time_step = 1.0)).nb_prey color: #green ;			// number of preys in the case where the integration time step is 1 is plotted in green		
				data 'Number of predators' value: first(LotkaVolterra_agent where (each.integration_time_step = 1.0)).nb_predator color: #red ; 	// number of predators in the case where the integration time step is 1 is plotted in red	
			}
			chart "Lotka Volterra Time Series - Integration time step = 0.1 " type: series background: #white position: {0,0.33} size:{1,0.33} x_range: 1000{
				data 'Number of preys' value: first(LotkaVolterra_agent where (each.integration_time_step = 0.1)).nb_prey color: #green ;				
				data 'Number of predators' value: first(LotkaVolterra_agent where (each.integration_time_step = 0.1)).nb_predator color: #red ;
			}
			chart "Lotka Volterra Time Series - Integration time step = 0.01 " type: series background: #white position: {0,0.66} size:{1,0.33}x_range: 1000{
				data 'Number of preys' value: first(LotkaVolterra_agent where (each.integration_time_step = 0.01)).nb_prey color: #green ;				
				data 'Number of predators' value: first(LotkaVolterra_agent where (each.integration_time_step = 0.01)).nb_predator color: #red ;
			}
		}
		display PhasePortrait  type: 2d {			
			chart "Lotka Volterra Phase Portrait - Integration time step = 1" type: xy background: #white position: {0,0} size:{1,0.33} {		// creation of a display to show phase portrait of the model, values are plotted at every step. Since there is more than one chart plotted in one display, every chart has a position and a size
			data 'Number of preys according to number of predators' value:{LV_agents[0].nb_prey, LV_agents[0].nb_predator} color: #black ;	// number of predators are plotted in black according to the number of preys in the case where the integration time step is 1		
			}
			chart "Lotka Volterra Phase Portrait - Integration time step = 0.1" type: xy background: #white position: {0,0.33} size:{1,0.33}{
			data 'Number of preys according to number of predators' value:{LV_agents[1].nb_prey, LV_agents[1].nb_predator} color: #black ;				
			}
			chart "Lotka Volterra Phase Portrait - Integration time step = 0.01" type: xy background: #white position: {0,0.66} size:{1,0.33} {
			data 'Number of preys according to number of predators' value:{LV_agents[1].nb_prey, LV_agents[1].nb_predator} color: #black ;				
			}
		}
	}
}

Home

  1. What's new (Changelog)

Platform

  1. Installation and Launching
    1. Installation
    2. Launching GAMA
    3. Updating GAMA
    4. Installing Plugins
  2. Workspace, Projects and Models
    1. Navigating in the Workspace
    2. Changing Workspace
    3. Importing Models
  3. Editing Models
    1. GAML Editor (Generalities)
    2. GAML Editor Tools
    3. Validation of Models
  4. Running Experiments
    1. Launching Experiments
    2. Experiments User interface
    3. Controls of experiments
    4. Parameters view
    5. Inspectors and monitors
    6. Displays
    7. Batch Specific UI
    8. Errors View
  5. Running Headless
    1. Headless Batch
    2. Headless Server
    3. Headless Legacy
  6. Preferences
  7. Troubleshooting

Learn GAML step by step

  1. Introduction
    1. Start with GAML
    2. Organization of a Model
    3. Basic programming concepts in GAML
  2. Manipulate basic Species
  3. Global Species
    1. Regular Species
    2. Defining Actions and Behaviors
    3. Interaction between Agents
    4. Attaching Skills
    5. Inheritance
  4. Defining Advanced Species
    1. Grid Species
    2. Graph Species
    3. Mirror Species
    4. Multi-Level Architecture
  5. Defining GUI Experiment
    1. Defining Parameters
    2. Defining Displays Generalities
    3. Defining 3D Displays
    4. Defining Charts
    5. Defining Monitors and Inspectors
    6. Defining Export files
    7. Defining User Interaction
  6. Exploring Models
    1. Run Several Simulations
    2. Batch Experiments
    3. Exploration Methods
  7. Optimizing Model Section
    1. Runtime Concepts
    2. Optimizing Models
  8. Multi-Paradigm Modeling
    1. Control Architecture
    2. Defining Differential Equations

Recipes

  1. Manipulate OSM Data
  2. Diffusion
  3. Using Database
  4. Using FIPA ACL
  5. Using BDI with BEN
  6. Using Driving Skill
  7. Manipulate dates
  8. Manipulate lights
  9. Using comodel
  10. Save and restore Simulations
  11. Using network
  12. Headless mode
  13. Using Headless
  14. Writing Unit Tests
  15. Ensure model's reproducibility
  16. Going further with extensions
    1. Calling R
    2. Using Graphical Editor
    3. Using Git from GAMA

GAML References

  1. Built-in Species
  2. Built-in Skills
  3. Built-in Architecture
  4. Statements
  5. Data Type
  6. File Type
  7. Expressions
    1. Literals
    2. Units and Constants
    3. Pseudo Variables
    4. Variables And Attributes
    5. Operators [A-A]
    6. Operators [B-C]
    7. Operators [D-H]
    8. Operators [I-M]
    9. Operators [N-R]
    10. Operators [S-Z]
  8. Exhaustive list of GAMA Keywords

Developing GAMA

  1. Installing the GIT version
  2. Developing Extensions
    1. Developing Plugins
    2. Developing Skills
    3. Developing Statements
    4. Developing Operators
    5. Developing Types
    6. Developing Species
    7. Developing Control Architectures
    8. Index of annotations
  3. Introduction to GAMA Java API
    1. Architecture of GAMA
    2. IScope
  4. Using GAMA flags
  5. Creating a release of GAMA
  6. Documentation generation

Tutorials

  1. Predator Prey
  2. Road Traffic
  3. 3D Tutorial
  4. Incremental Model
  5. Luneray's flu
  6. BDI Agents

Community

  1. Team
  2. Projects using GAMA
  3. Scientific References
  4. Training Sessions

Versions of GAMA

Resources

  1. Videos
  2. Conferences
  3. Code Examples
  4. Pedagogical materials
Clone this wiki locally