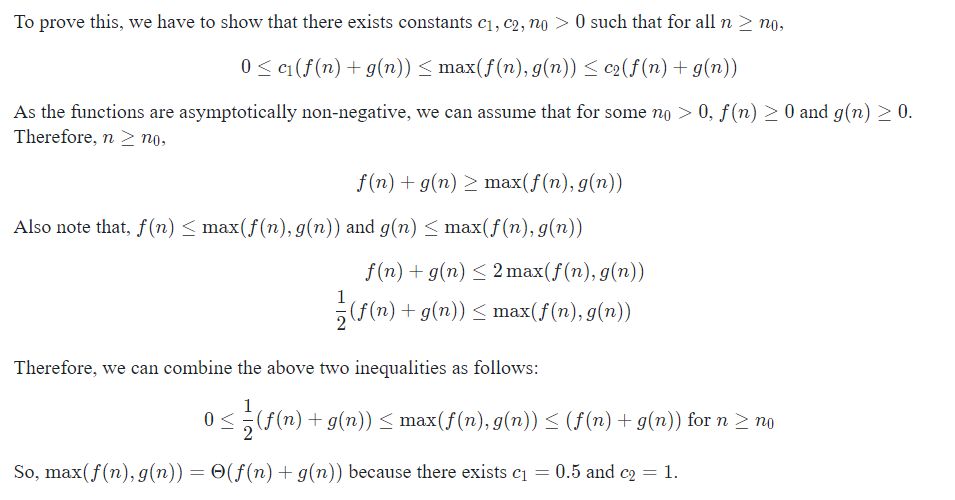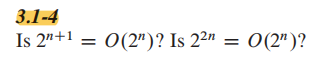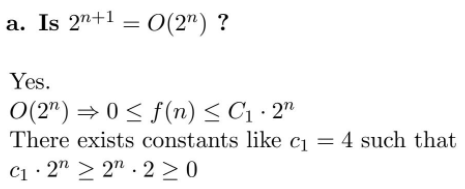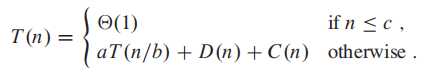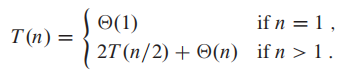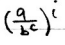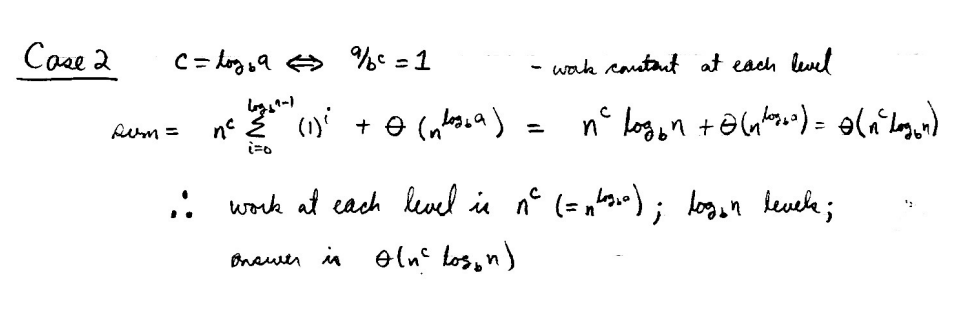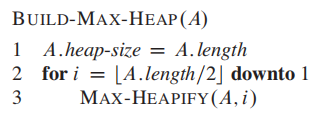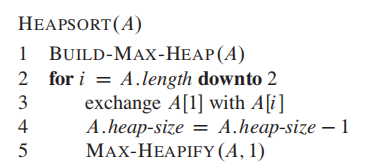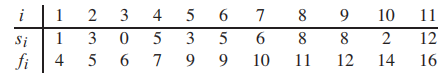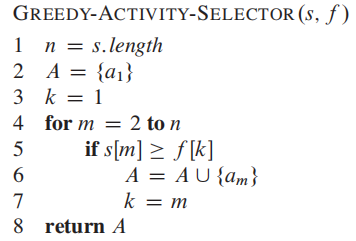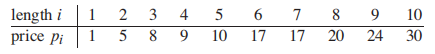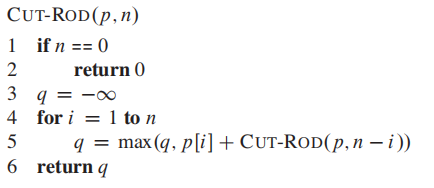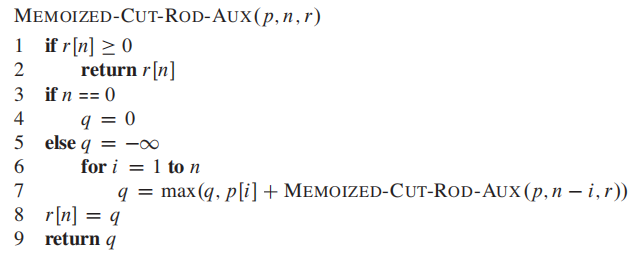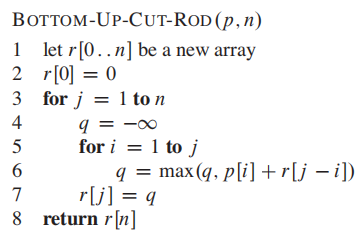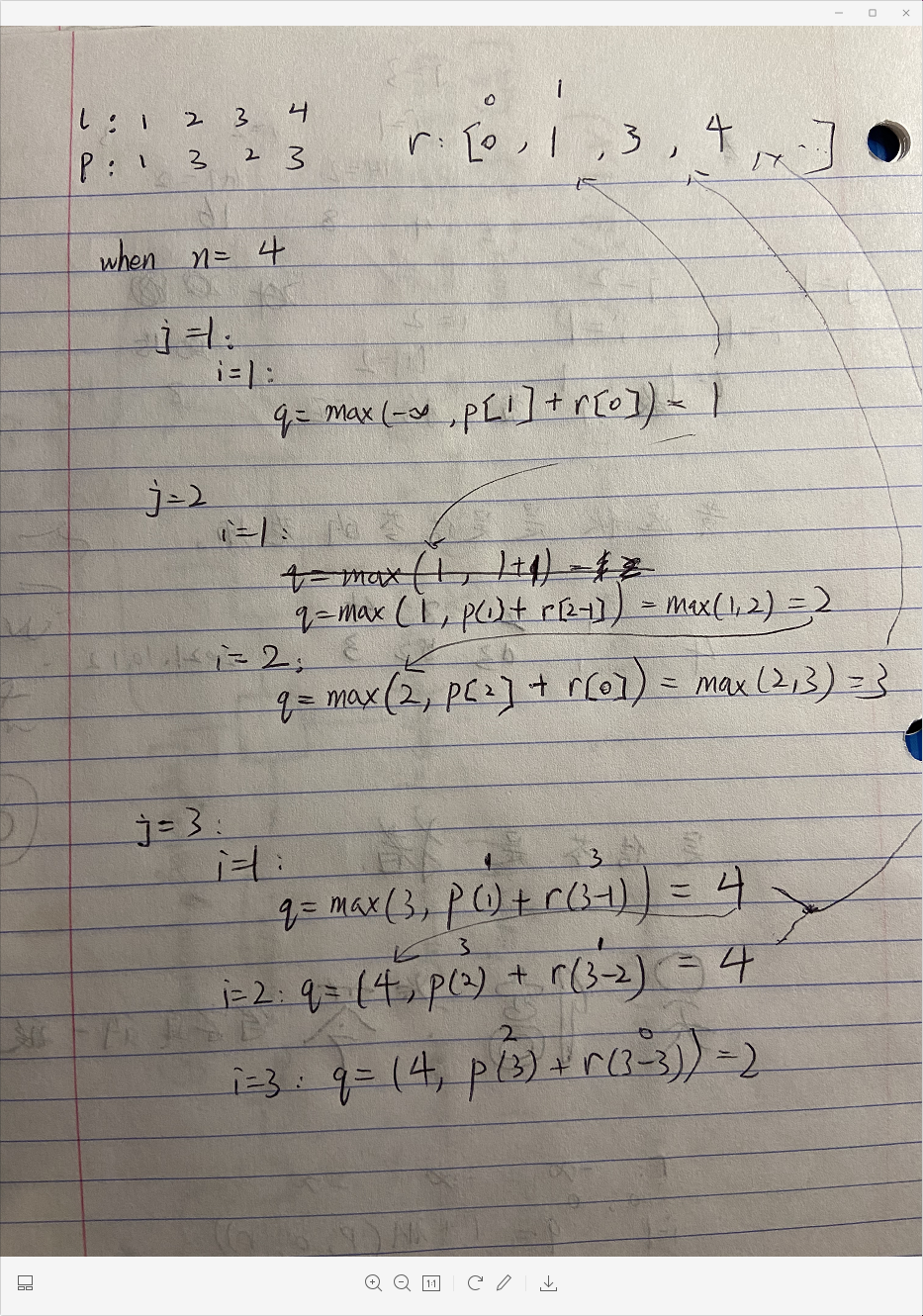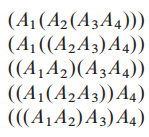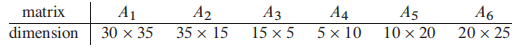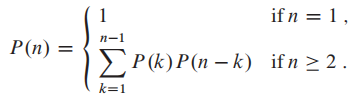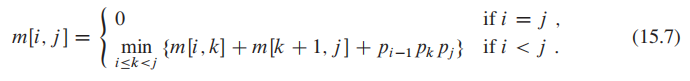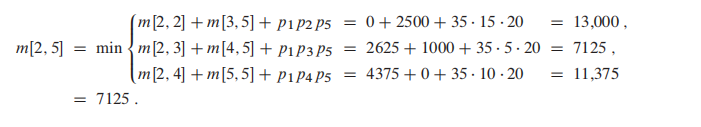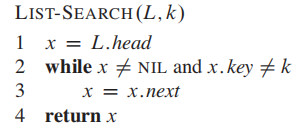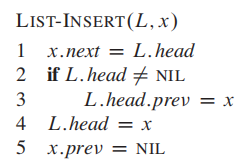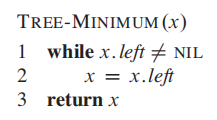- 笔记按照NEU CS 5800 Prof. Virgil Pavlu 的教授顺序来排序，有掠过原书的一些章节。
- notes by
Yiqiu Huang
What is
-
we call it T(n) = number of computational steps required to run the algorithm/program for input of size n
-
we are interested in order of growth, not exact values
- for example T(n) = Θ(n2) means quadratic running time
- T(n) = O(n logn) means T(n) grows not faster than CONSTnlog(n)
Why Asymptotic notation?
Even when we use asymptotic notation to apply to the running time of an algorithm, we need to understand which running time we mean.
原文定义如下：
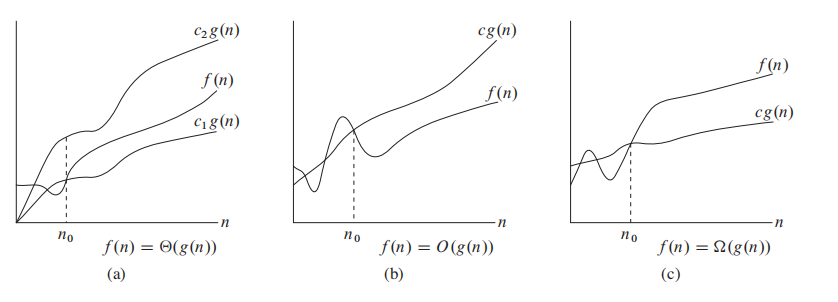
For a given function g(n), we denote by
$\Theta$ (g(n)) the set of functions:
$\Theta(g(n))$ = {$f(n)$: there exist positive constants$c_1$ ,$c_2$ , and$n_0$ such that$0\leq c_1g(n) \leq f(n) \leq c_2g(n)$ for all n$\geq$ n0 }如果满足如上条件，我们说 g(n) is an asymptotically tight bound for f(n)
简单来说就是n到一定大小以后(
注意，$\Theta(g(n))$ 本身描述的是一个集合，所以你可以这么写： $$ f(n) \in \Theta(n) $$
不过我们习惯这么写： $$ f(n) = \Theta(n) $$ 这样写有自己独特的优势。
原文定义如下：
For a given function g(n), we denote by
$\Theta$ (g(n)) the set of functions:
$\Theta(g(n))$ = {$f(n)$: there exist positive constants$c$ and$n_0$ such that$0\leq f(n) \leq c g(n)$ for all n$\geq$ n0 }如果满足如上条件，我们说 g(n) is an asymptotically upper bound for f(n)
简单来说就是n到一定大小以后(
最简单的说，$O$ notation 就像是小于号，它描述的是上界。
平时我们习惯用大O表示法来表示runtime，比如寻找一个数组的最大值，我们说runtime 是 O(n)；
这么说不完全严谨，因此O(n)描述的是上界(upper bound)，无法说明how tight that bound is, 你说寻找最大值的算法是$O(n^2)$,$O(n^3)$也没问题。
原文定义如下：
For a given function g(n), we denote by
$\Theta$ (g(n)) the set of functions:
$\Theta(g(n))$ = {$f(n)$: there exist positive constants$c$ and$n_0$ such that$0 \leq c g(n) \leq f(n)$ for all n$\geq$ n0 }如果满足如上条件，我们说 g(n) is an asymptotically lower bound for f(n)
简单来说就是n到一定大小以后(
答案：
本质上，你要证明常数存在，来证明公式正确。
类似的技巧：
分治法：
Divide the problem into a number of subproblems that are smaller instances of the
same problem.
Conquer the subproblems by solving them recursively.
Combine the solutions to the subproblems into the solution for the original problem.
与我们熟悉的 Mergesort 一一对应：
Divide: 把长度为 n 的序列切分为两个长度为
$\frac{n}{2}$ 的序列Conquer: 递归的调用mergesort来sort sequence。(原文：Sort the two subsequences recursively using merge sort)
Combine: 合并两个sorted sequence
Suppose that our division of the problem yields a subproblems, each of which is 1/b the size of the original.
- 注意，Mergesort的a = b = 2, **很多分治法a 并不等于 b 更不等于 2
- 注意后面这句话: each of which is 1/b the size of the original 他的意思是每个子问题的size都是原来的1/b，那么随着递归的进行，子问题的size就是:
可以思考一下这个 ? 应该是什么
用白话来说就是，mergesort产生了2个size是(n/2)的subproblem。
假设mergesort的runtime 是T(n),我们有 a 个size 为b/n 的子问题，因此我们需要 aT(n/b) 来解决他们。
除此之外，我们需要 D(n) 来divide the problem into subproblem, 以及 C(n) 来combine我们的solution from all subproblem, 我们的总时间为：
这段比较重要，还是原汁原味吧：
Divide: The divide step just computes the middle of the subarray, which takes
constant time. Thus, D.n/ D ‚.1/.
Conquer: We recursively solve two subproblems, each of size n=2, which contributes 2T(n/2) to the running time.
Combine: We have already noted that the MERGE procedure on an n-element
subarray takes time ‚.n/, and so C.n/ D ‚.n/.
Divide: mergesort 在 diide 时只计算出中位数，所以是contant time, D(n) = 1
Conquer: 我们递归的解决两个子问题，每一个子问题的size是 n/2, 因此是 2T(n/2)
Combine: combine的本质就是遍历，谁小谁先进sorted array, 因此
$C(n) = \Theta(n)$
因此：
递归法往往能写成以下的格式：
主要有三种方法求解分治法的时间复杂度
In the substitution method, we guess a bound and then use mathematical in�
duction to prove our guess correct.
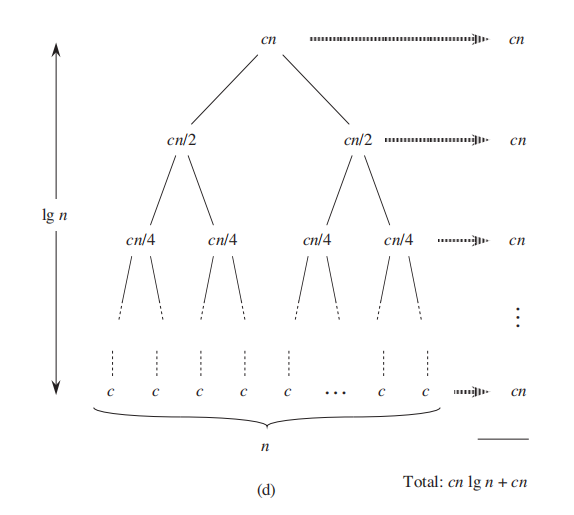
The recursion-tree method converts the recurrence into a tree whose nodes
represent the costs incurred at various levels of the recursion. We use techniques
for bounding summations to solve the recurrence.
The master method provides bounds for recurrences of the form
$T(n) = aT(\frac{n}{b}) + f(n)$
使用Master Theorum可以快速求出常见递归的时间复杂度。
比较重要，比较实用，比较递归参数的大小得到时间复杂度：
Binary search, Mergesort 的runtime 可以轻松的求出。
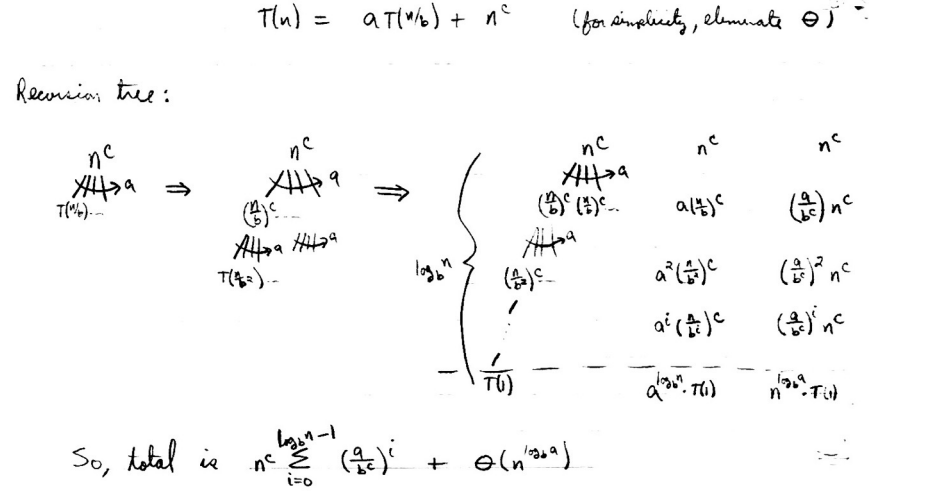
首先求出递归的数学表达：
对于关键项
来说，有三种表达 <1,=1,>1,so three
算法本身不做介绍。
worst running time is O(log n)
二叉树的本质是一种比较算法, 在这里先引入这个概念:
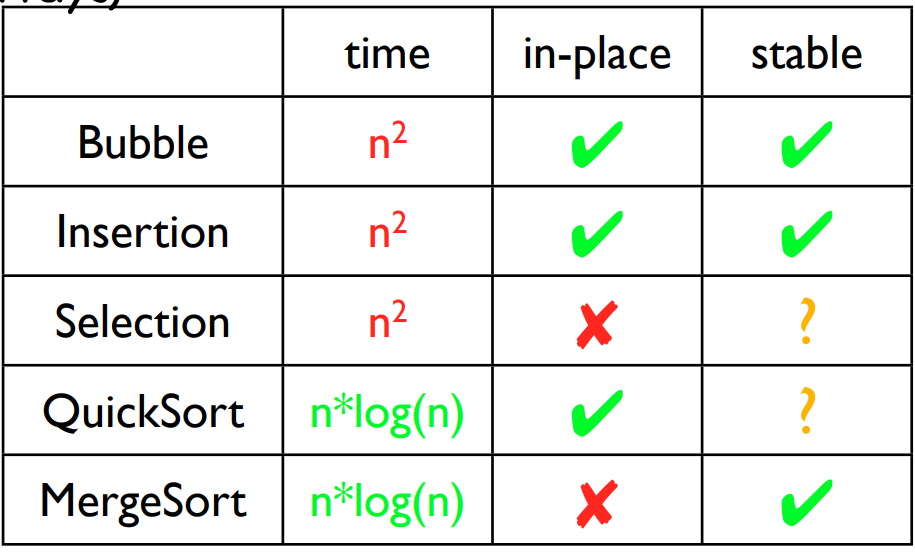
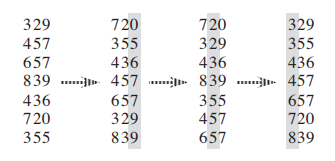
Insertion sort
最大堆性质：
In a max-heap, the max-heap property is that for every node i other than the root:
为了满足最大堆性质，你需要调用:
****:
这段代码的逻辑就是找出
- 如果最大值是$i$，那么左右子树小于$i$, 满足max-heap property,无事发生。
- 如果不是，将$i$与largest 交换；交换后当前node满足max-heap, 但是子树不一定满足；因此对子树继续进行max-heapify
MAX-HEAPIFY 复杂度分析：
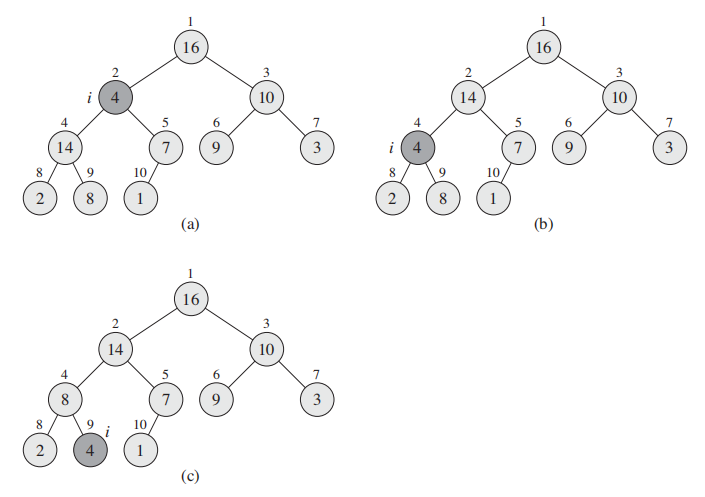
根据heap(二叉树)的性质，$A[(\frac{n}{2} + 1) ... n]$都是叶节点；因此从$ \frac{n}{2}$ downto 1进行heapify
这样就完成了BUILD-MAX-HEAP。
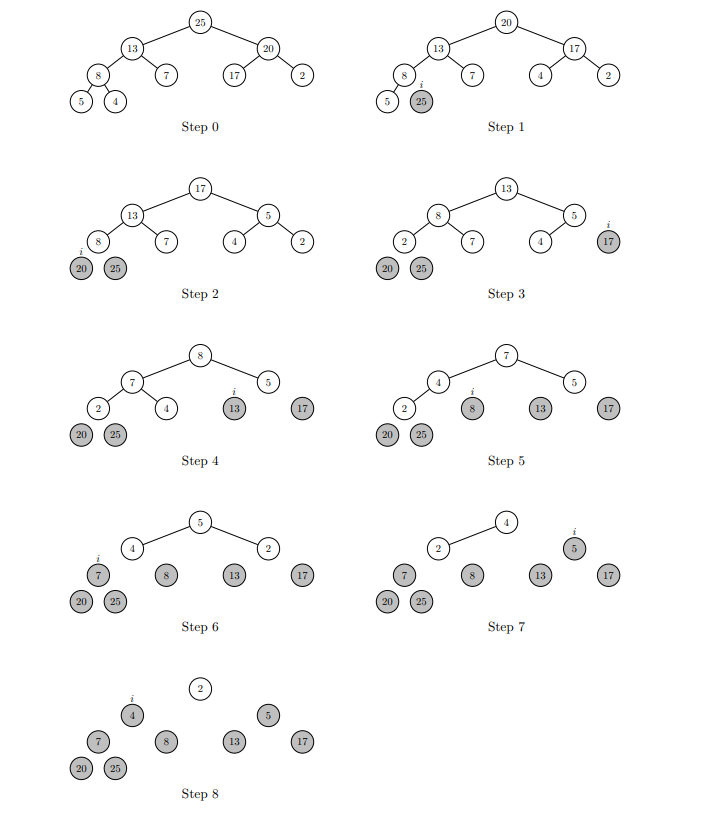
下面来自例题：
答案：
Heapify -> 得到最大值 ->换到最后一位，不再管他，size - 1 -> 循环
A divide-and-conquer algorithm with worst-case running time of
Partition 是 quicksort 最重要的机制。
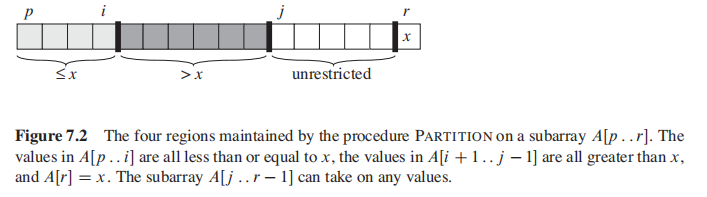
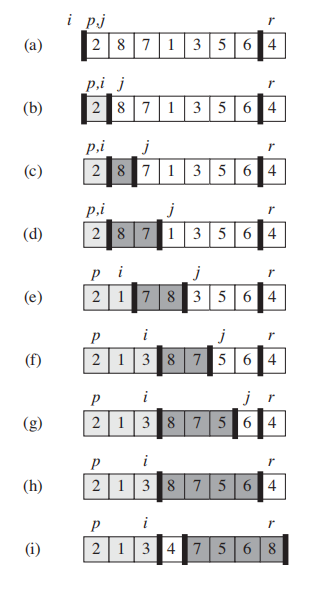
Partition 会选择 x = A[r] 作为 pivot element。你要理解的是在Partition的过程中，有四个区域，先理解这个思路，伪码就能看懂了：
[j,r-1] 还没看到的区域
[p, i] 小于pivot 的区域
[i,j] 大于pivot的区域
[r] pivot element
注意，partition返回的是i + 1.
Worst-case partitioning
The worst-case behavior for quicksort occurs when the partitioning routine produces one subproblem with
老师讲的很少，这块不复习了。
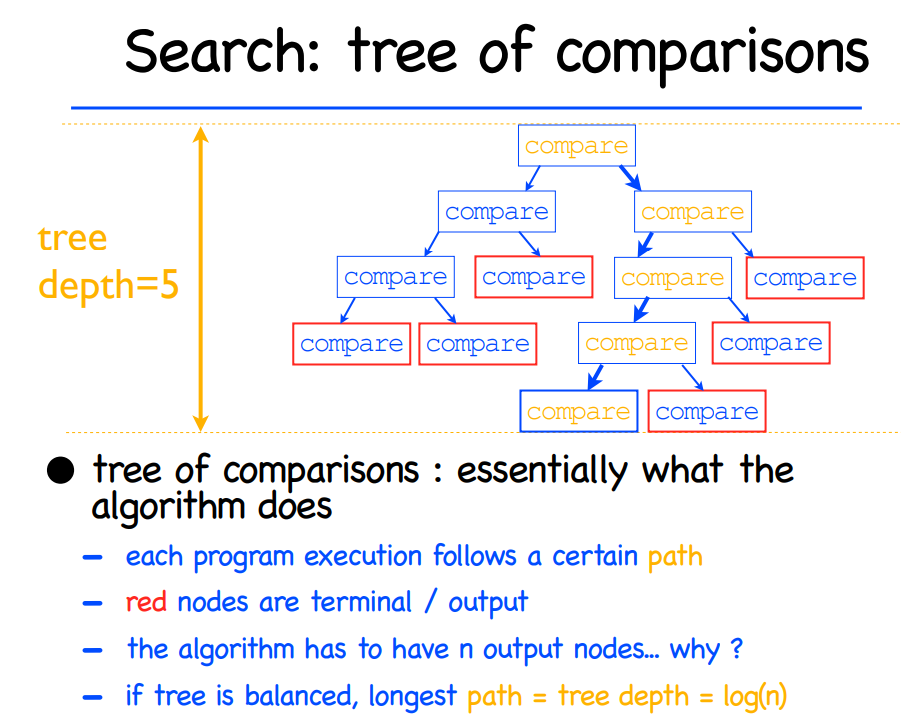
常见的算法主要是比较算法(comparison sort)，比如mergesort在merge的部分需要比较两个数字的大小来排序。comparison sort 可以用下图的例子来类比：
求出树的高度h**(i.e., 抵达leaf的worst case时间)**,就是排序的worst case时间。
输入n的permutation 为n!, 参考下图的决策树，运行时间即为h，可以得出 $$ h = \Omega(n lgn) $$ 摘一段原文：
为什么
Some intuition about why: $$ lg(n!) = \Theta(n\cdot lgn) $$ 你需要记住
and
在选择最小值的算法上，我们都知道：
遍历数组，经过n-1次的比较我们可以找到最小值。This is the best we could do.
The general selection problem appears more diffificult than the simple problem of finding a minimum. Yet, surprisingly, the asymptotic running time for both problems is the same: $$ \Theta(n) $$
RANDOMIZED-SELECT类似quickSort,也是一种divide-and-conquer alg.
The following code for RANDOMIZED-SELECT returns the i smallest element of array A[p...r]
-
Line 1 & Line 2: 如果array长度为1，那直接返回array中的值
-
Line3: 类似quickSort的partition, 选择pivot，让A[p...q-1]的小于pivot, 让A[q+1,r]的值大于pivot, **A[q]**就是pivot number
-
Line4: 计算k(即A[p...q-1]的长度 + 1)
-
Line5: 如果 i == k,即你要的i th 等于 k,找到了答案，返回A[q]
-
Line7, 8,9: 否则，根据 i与k的关系继续调用RANDOMIZED-SELECT(if i>k, the desired element will lies in high partition part)
The worst-case running time for RANDOMIZED-SELECT is $$ \Theta(n^2) $$
select algorithm 应该就是median-of-medians,但是没有在wiki上得证。
大致思路：
- Divide the n elements of the input array into n/5 groups of 5 elements each gourp
- Find the median of each of the n/5 groups by insertion sorting
通常找第
Use a divide and conquer strategy to efficiently compute the
$i^th$ smallest number in an unsorted list of size n.
好文：https://brilliant.org/wiki/median-finding-algorithm/
给定A的，找到4th smallest element:
把A分成n/5份，保证每个subgroup有5个元素
分别求中位数：
Sort M:
求出M 中的中位数 len(M)/2 = 1, which is 76 (这一步就是所谓median-of-medians)
使用76作为pivot, partition(A)，左边元素小于pivot index(76的idx是5)，右边大于pivot index;
76的index是5, 5 > 3, 所以继续，在左半边(p, q-1)继续partition，也就是
最后只剩5个元素的时候会直接排序，书中说小于5个的元素排序时间复杂度是n，idk y。
注：sort小于5的array时间为O(n)? WTF? 这点我也没搞懂
详细分析参考上方的原文链接。以下为intuition：
-
T(n/5) + O(n):
我们把n分成了n/5的subproblem, partition需要上述的时间，参考quickSort。
-
T(7n/10)
在M(median list, 参考example M)中，M的长度为n/5 ,因此M中有一半的元素小于p(M的中位数，也就是中位数的中位数)，也就是n/10，这一半的元素本身又有2个元素小于自己，因为这些元素本身是median of 5 element，因此有n/10 + 2* n/10 = 3n/10 的元素小于p。
因此在worst case情况下，算法每次都会recurse on the remaining 7n/10的元素。
根据master thoerum, 得出time complexity O(n)
Intro: why greedy algorithm?
For many optimization problems, using dynamic programming to determine the best choices is overkill;
A greedy algorithm always makes the choice that looks best at the moment. That is, it makes a locally optimal choice in the hope that this choice will lead to a globally optimal solution.
Greedy algorithms do not always yield optimal solutions, but for many problems they do
目标：我们要选择最大activities数量的集合，activities时间不能重合。（maximum-size set of activities.）
我们有n个activities,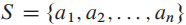
每个activity a i has a start time f i and a finish time s i
你选择的集合中，a i 和a j 需要是兼容的(compatible), 也就是他们时间区间 [si,fi] 不能有重合。
比如 set :{a 1, a 2} 是一个不合格的set, 因为 a 1 的区间[1,4] 和 a 2 的区间[3,5] 就在[3,4]上有重合，我们要避免这样的overlap,选出最大的子集。
贪心算法的核心在于，我们要找出最好的greedy choice。在这个问题中，我们每一步都需要:
we should choose an activity that leaves the resource available
for as many other activities as possible.
这句话的意思在后来的另一个例子找硬币中也能体现出来，现在先往下走。
Greedy Algorithm的核心：
- Greedy choice: 每次都寻找最早结束的activity, Let's call it a earliest
- Subproblem: only consider activity start after a earliest have finished. (排除有overlap的activity)
剩下的，交给递归recursive
![image-20211008004254723]()
(#注意，书中假设activity list: n已经按照finish time list: f 进行升序的排序），因此time complexity O(n))：
It also assumes that the input activities are ordered by monotonically increasing finish time.
看看就行：
经过经典的递归greedy algorithm解法，经典的下一步就是把rucursive变成iterative的解法。
贪心算法的核心性质：
Greedy-choice property
The first key ingredient is the greedy-choice property: we can assemble a globally
optimal solution by making locally optimal (greedy) choices.
这个性质比较好理解，这也是greedy和DP的主要区别。
Optimal substructure
A problem exhibits optimal substructure if an optimal solution to the problem
contains within it optimal solutions to subproblems.
这个性质可能需要时间消化，以activity-selection问题为例：
if an optimal solution to subproblem
$S_{ij}$ includes an activity$a_k$ , then it must also contain optimal solutions to the subproblems$S_{ik}$ and$S_{kj}$
下方是书中给出的步骤：
总结
- 贪心算法only make locally optimal choiceœ, 部分的贪心算法不能保证走向 global-optimal solution, 但我们只关心那些能保证走向global-optimal solution的算法。
- 贪心算法的核心在于寻找strategy, 你需要证明你的贪心策略是正确的。
证明贪心算法需要证明以下两个性质
Greedy-choice property
The first key ingredient is the greedy-choice property: we can assemble a globally optimal solution by making locally optimal (greedy) choices.
Optimal substructure
A problem exhibits optimal substructure if an optimal solution to the problem contains within it optimal solutions to subproblems.
- Dynamic programming, like the divide-and-conquer method, solves problems by
combining the solutions to subproblems.
- In contrast, dynamic programming applies when the subproblems overlap—that is, when subproblems share subsubproblems.:
divide-and-conquer algorithm does more work than necessary, repeatedly solving the common subsubproblems.
dynamic-programming algorithm solves each subsubproblem just once and then saves its answer in a table, thereby avoiding the work of recomputing the answer every time it solves each subsubproblem.
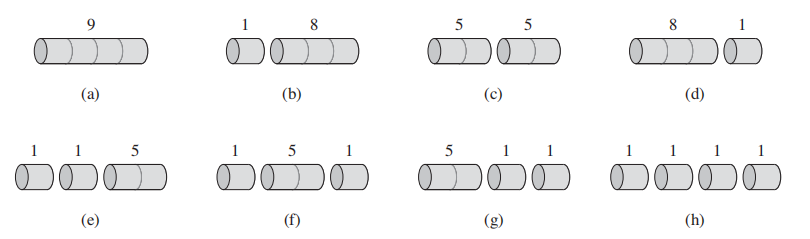
切绳子问题定义如下：
给定一个总长度为n的绳子，给定价格
Task: 如何切分绳子，使得总价值
比如给定长度为4的绳子，绳子可以切分的长度和根据上图计算得出的总价值分别如下：
可以看出 (c)的总价值为10，是最大的。
切绳子问题展现出了optimal substructure:
原始问题是 problem of size(n), 当我们第一次cut之后，我们就在解决两个独立的子问题。
optimal solutions to a problem incorporate optimal solutions to related subproblems, which we may solve independently.
i.e. 子问题的最优解被包含在了全局问题的最优解中。
Method 1: Brute force
长度为n的绳子共有
Method 2: Recursive top-down implementation
@param:
**p** : array p[1..n] of price
n: 长度n
#comment
3：init max value to -infinity
4-5: compute max value q
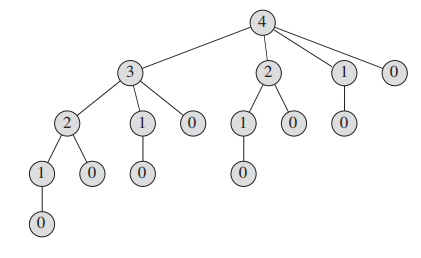
CUT-ROD is very inefficient. it solves the same subproblems repeatedly.
下图展示了 CUT-ROD(p, 4)的递归，可以看到相同的子问题被反复的计算。
时间复杂度T(n) =
Method 3 dynamic programming for optimal rod cutting
动态规划出现了！
核心思想：每个子问题只解决一次，使用额外的空间来保存子问题的solution。
We just look it up, rather than re-compute it.
It is a time-memory trade-off.
There are usually two equivalent ways to implement a dynamic-programming
approach.
The fifirst approach is top-down with memoization.
The first approach is top-down with memoization. In this approach, we write the procedure recursively in a natural manner, but modifified to save the result of each subproblem (usually in an array or hash table). The procedure now first checks to see whether it has previously solved this subproblem. If so, it returns the saved value, saving further computation at this level; if not, the procedure computes the value in the usual manner. We say that the recursive procedure has been memoized;it “remembers” what results it has computed previously.The second approach is the bottom-up method.
This approach typically depends on some natural notion of the “size” of a subproblem, such that solving any particular subproblem depends only on solving “smaller” subproblems. We sort the subproblems by size and solve them in size order, smallest first. When solving a particular subproblem, we have already solved all of the smaller subproblems its solution depends upon, and we have saved their solutions. We solve each subproblem only once, and when we first see it, we have already solved all of its prerequisite subproblems.
简单来说，二者差别如下：
top-down方法先检索是否有该subproblem的答案；
如果有，使用该答案。
否则, 计算该答案，进入递归。
而bottom-up方法使用问题大小的自然顺序(natural notion of the size of problem)，**从最小的问题开始， 自底向上 的逐一解决，**因此解决到大问题时，之前的小问题已经解决完了。
原文的详细定义点开上方折叠。
**Pseudocode for the top-down CUT-ROD procedure: **
top-down:
bottom-up:
下图为bottom-up 方法我个人的部分演算：
我们熟知的矩阵乘法的伪码如下：
假设我们要连乘矩阵 <$A_1,A_2,A_3,A_4$>, 我们有以下5种方法, i,e, we can fuuly parenthesize the product in 5 distinct ways:
现在我们来分析假设我们要连乘矩阵 <$A_1,A_2,A_3$> ，他们的维度分别为**<10 x 100, 100 x 5, 5 x 50>**。
parenthesization ** <$((A_1,A_2),A_3$)> 中，第一次括号内运算会有10 * 100 * 5 = 5000 次运算，然后再有 10 * 5 * 50 = 2500 次运算，总共有7500**次的运算。
而<$(A_1,(A_2,A_3)$)>,第一个括号 100 * 5 * 50 = 25000次运算，之后有10 * 100 * 50 = 50000 的运算，总共有75000次运算，比第一个快十倍。
如下，我们引出矩阵连乘问题：
Our goal is to determine an order for multiplying matrices that has the lowest cost.
即，找出最快矩阵连乘的顺序。
假设我们有下方的矩阵：
注意，其中，矩阵$A_i$的维度是
Method 1 brute-force 穷举法
根据矩阵数量，这是inefficient的递归公式：
**
Method 1 Applying dynamic programming
记得之前的四个步骤：
现在大概跟一遍：
Step 1: The structure of an optimal parenthesization
假设我们有如下optimal 的待乘矩阵
因为如果$A_i,A_{i+1},...,A_{k}$ 有更好的方法，那么
上面的方法是反证法（contradiction）。
Step 2: A recursive solution
如果我们在$A_k$ (i < k < j) 将待乘矩阵分开，那么我们会得到两个子问题$A_i,A_{i+1},...,A_{k}$ 和
我们让 m[i, j] 来表示全局问题的最优解（即最小的multiplication 次数），两个子问题即为 m[i,k], m[k+1,j];
合并两个子问题的product
这样，我们的问题变成了
Step 3: Computing the optimal costs
回顾一下斐波那契数列，斐波那契数列也可以用动态规划来表示；
如果只用递归的方法调用斐波那契数列，递归的过程中，F(5)和F(8)都会重新计算F(4),F(3)....
动态规划的标志就是他储存了已经计算过的答案来防止re-compute。
假设我们有下方的矩阵：
注意，其中，矩阵$A_i$的维度是
bottom-up approach：
- set
$m[i,i]$ = 0 ($m[i,i]$ 代表矩阵乘以矩阵本身，连子问题都不算，只是trivial), 这也是为什么源码的n-1，n=6的问题我们只需要计算五个就好了 - compute
$m[i,i+1]$ for$i = 1,2,...,n-1$ - then compute
$m[i,i+2]$ for$i = 1,2,...,n-1$ , and so forth
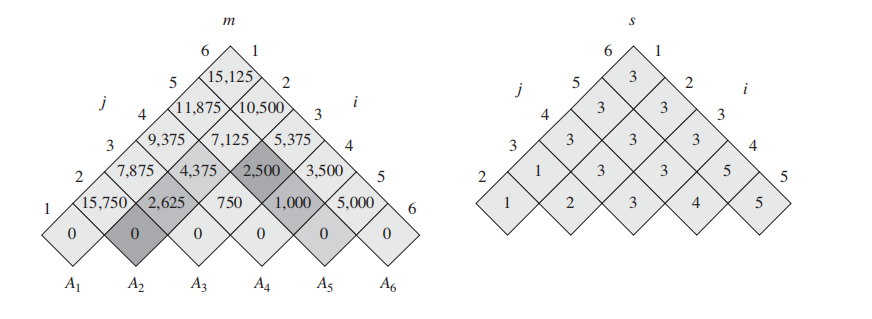
作为一个bottom-up的DP, 我们每次都在尝试想上计算；比如当算到$m[2,5]$时， 我们其实在做以下事情
上图左侧的table即为伪码中的 m table， 右边的是 s table。
m表只给出了m[i,...,j] 的对应最优计算次数，并没有告诉我们 m[1,6] 的过程应该怎么进行切分；因此我们需要右边的 s table 来告诉我们。
**$s[i,j]$ 记录了每一次的最优切分k。**通过s表递归的寻找k,我们就能知道最优切分。
如果上面你看懂了，下面这三张图你可以跳过。
这代码
好一个bottom-up：
Optimal substructure
A problem exhibits optimal substructure if an optimal solution to the problem contains within it optimal solutions to subproblems.
有些问题没有Optimal substructure性质，比如给定一个没有权值的有向图(directed graph)：
现在有两个问题，定义如下：
-
无权值的最短路径问题（Unweighted shortest path）：找到某顶点u到某顶点v的 最少边的数量。
（英文比较好看懂：Find a path from u to v consisting of the fewest edges.）
- 无权值的最长路径问题(Unweighted longest simple path:): 找到某顶点u到某顶点v的 最多边的数量。
哪个问题有optimal structure呢？
问题1有。
查缺补漏：图的定义如下：
A directed graph (or digraph) is a set of vertices and a collection of directed edges**(边)** that each connects an ordered pair of vertices**(顶点)**.
一句话说，由顶点 set:V 和 边 set :E组成
**Unweighted shortest path:**3
Find a path from u to consisting of the fewest
edges. Such a path must be simple, since removing a cycle from a path pro�
duces a path with fewer edges.
作者很懒还没写完
作业以及课本包含一些经典DP的leetcode题目，如下：
516. Longest Palindromic Subsequence
887. Super Egg Drop (took me a long while...for real...)
得从brute force开始：
https://leetcode.com/problems/super-egg-drop/discuss/159079/Python-DP-from-kn2-to-knlogn-to-kn
到这位大神的：
https://leetcode.com/problems/super-egg-drop/discuss/158974/C%2B%2BJavaPython-2D-and-1D-DP-O(KlogN)
- stack:
last-in,first-out
Methods: push , pop
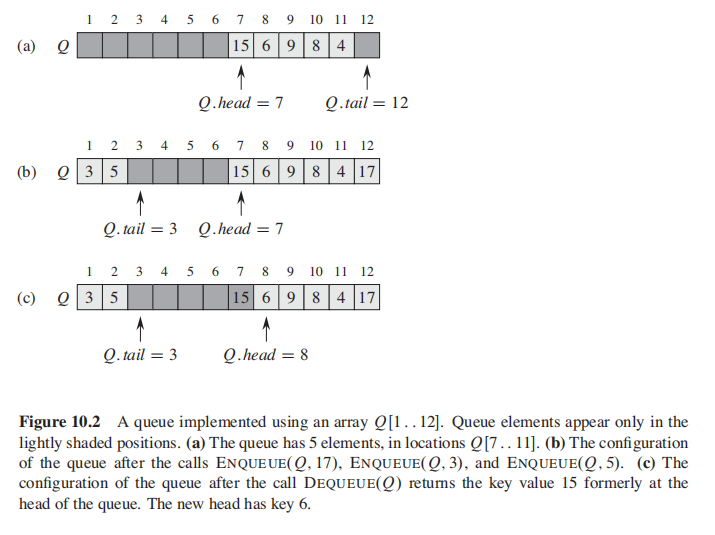
- queue
queue: first-in, first-out
Methods: deque, enque
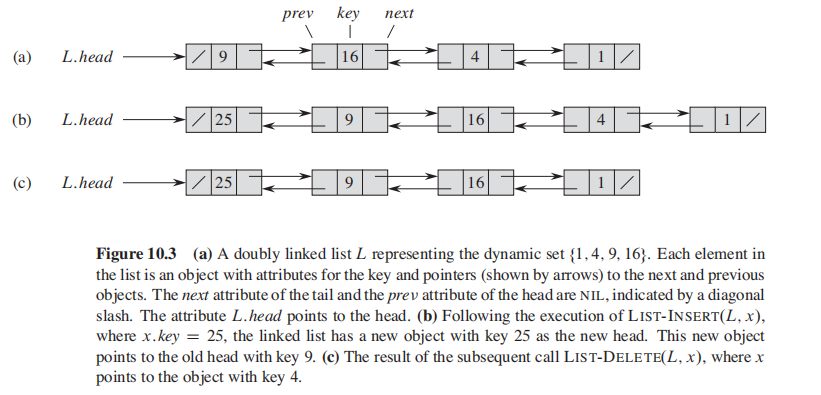
The order in alinked list is determined by a pointer.
Methods: search, insert, delete
搜索：
时间复杂度：$O(n)$
插入：
注意，这个是从前面插入；
不用遍历，因此时间复杂度是
删除：
需要先使用Search功能，因此worst case时间复杂度是$O(n)$
好像没啥说的
- Binary Search Tree
inorder tree walk. This algorithm is so named because it prints the key of the root of a subtree
between printing the values in its left subtree and printing those in its right subtree.
Min
最小值就是找到最左的节点
Max
最大值就是找到最右的节点
Successor and Predecessor是个啥？
**Successor **
If all keys are distinct, the successor of a node x is the node with the smallest key greater than x.key.
即，x的successor是刚好大于x的那个节点；
为了找到这个节点：
我们的目标是找到刚好比x大的元素，所以：
-
如果x的右子树不为空，那么找到右子树中的最小元素即可；
要找到右子树中的最小元素，对着x.right调用
min方法即可； -
如果x的右子树是空的，那么sucessor只能在x的头上；此时又有两种情况：
- 假设y是x的parent, 若x是y的左子树，说明x<y,那么直接返回y;
- 否则, x是y的右子树，x>y, 再往上走；(如果走到根节点，就会返回NIL)
Predecessor
与Successor 相反，Predecessor是刚好小于 x 的节点；
假设我们要找的节点x是存在于树中的。
因此:
- 如果x.left
$\neq$ NIL, 那么Predecessor就是x.left中的最大值; - 否则，Predecessor不存在；
书中BST涉及的一些leetcode:
110.Balanced Binary Tree：https://leetcode.com/problems/balanced-binary-tree/
比较tricky地方在于，检查BST是否平衡，不只是统计根节点的左右子树最大高度差，因为可能发生这种情况：
对于根节点来说，height(左子树) - height(右子树)的高度差小于2；
但是对于节点10来说，高度差是2，破坏了平衡；
因此，你需要对每一个节点都check balance。
- Insert into a Binary Search Tree: https://leetcode.com/problems/insert-into-a-binary-search-tree/
找到位置插入即可，优雅的代码来自：
这哥们老想写成一行，为了可读性我给他展开了：
class Solution(object):
def insertIntoBST(self, root, val):
if root == None:
return TreeNode(val)
if root.val > val:
root.left = self.insertIntoBST(root.left,val)
else:
root.right = self.insertIntoBST(root.right,val)
return root
- Delete Node in a BST： https://leetcode.com/problems/delete-node-in-a-bst/
原文写的太复杂了，用到了transplant; 因此使用leetcode大哥的；
删除操作有3个case;
-
如果节点没有children, 那么直接删除；
-
如果节点没有左children, 那么右children直接顶上来;
-
否则，找到左children中的最大值，并且顶上去；
代码来自：
class Solution:
def deleteNode(self, root, key):
"""
:type root: TreeNode
:type key: int
:rtype: TreeNode
"""
if not root:
return
# we always want to delete the node when it is the root of a subtree,
# so we handle left or right according to the val.
# if the node does not exist, we will hit the very first if statement and return None.
if key > root.val:
root.right = self.deleteNode(root.right, key)
elif key < root.val:
root.left = self.deleteNode(root.left, key)
# now the key is the root of a subtree
else:
# if the subtree does not have a left child, we just return its right child
# to its father, and they will be connected on the higher level recursion.
if not root.left:
return root.right
# if it has a left child, we want to find the max val on the left subtree to
# replace the node we want to delete.
else:
# try to find the max value on the left subtree
tmp = root.left
while tmp.right:
tmp = tmp.right
# replace
root.val = tmp.val
# since we have replaced the node we want to delete with the tmp, now we don't
# want to keep the tmp on this tree, so we just use our function to delete it.
# pass the val of tmp to the left subtree and repeat the whole approach.
root.left = self.deleteNode(root.left, tmp.val)
return rootso f**king clean！
见过的最优雅代码之一了！
https://docs.python.org/2/library/functions.html#hash
Python 官方文档：
用来for loop 比较 key 值是否相等的
使用pyhon试试 $hash $ 函数：
Direct addressing is a simple technique that works well when the universe U of keys is reasonably small.
直接寻址法 适用于key比较少的时候。
这样的方法同时记住了 key 和 data（而不是data的address） ，非常占用空间；
Python用久了让人有 dict 很简单的错觉，所以这个内容让我思考了很久。
建议先看一下下文：
https://zhuanlan.zhihu.com/p/74003719
With direct addressing, an element with key k is stored in slot k.
With hashing, this element is stored in slot h(k); that is, we use a hash function h to compute the
slot from the key k.
Here, h maps the universe U of keys into the slots of a hash
table T[0 .. m-1]:
h: U ---> {0,1, ... , m-1}
简而言之：
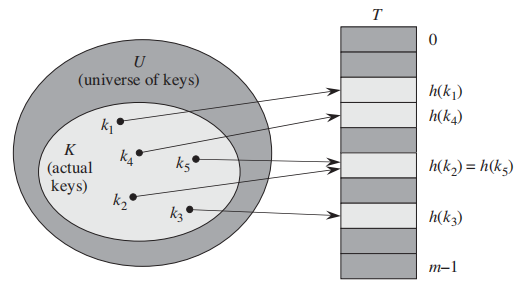
An element with key k hashes to slot h(k);
hash function减少了indices的范围；
但是有时候两个key会被match到一个slot里面；这就是一个 collision; 参考上图。
比如我们的 hash(x) = x%10, 这样的话25 和 35就会被match到同一个slot上，这就是一个冲突；
发生冲突并不可怕，有一些有效的方法能化解冲突带来的结果；（冲突本身是不可能解决的）
哈希算法最重要的特点就是：
- 相同的输入一定得到相同的输出；
- 不同的输入大概率得到不同的输出。
下面介绍原书中提供的最简单的冲突解决方法；
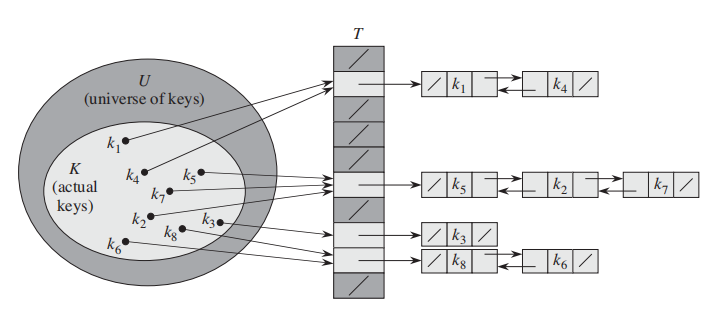
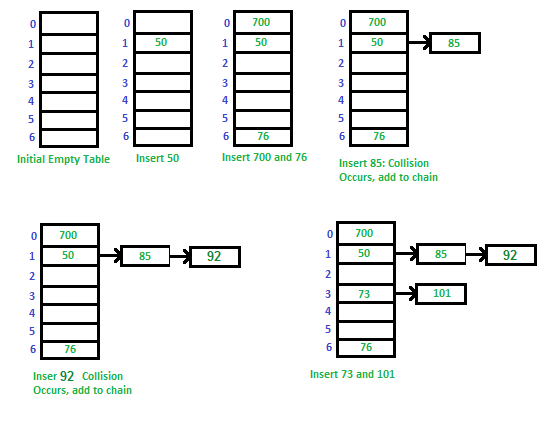
1. Chaining:
让每一个key都对应一个linked list;
一个例子：
2. 开放寻址法(open addressing):
什么是好的 hash function?
- simple uniform hashing: each key is equally likely to hash to any of the m slots
如果完全随机的插入slot, 就可以满足这个条件；
Most hash functions assume that the universe of keys is the set N= {0,1,2, ......}
of natural numbers. Thus, if the keys are not natural numbers, we find a way to
interpret them as natural numbers.
比如最简单的division method: $$ h(k) = k \mod m $$
A hashing technique perfect hashing if $O(1)$memory accesses are required to perform a search in the worst case.
为了做到完美哈希，第一个因素和之前的方法是一样的：选择一个好的 hash function $ h $ 把
之后，除了使用chaining 搭建新 linked list的方法之外，转而使用一个小的第二哈希表 secondary hash table
**Theorem： **
Suppose that we store n keys in a hash table of size
$m = n^2$ using a hash function$h$ randomly chosen from a universal class of hash functions.Then, the probability is less than
$1/2$ that there are any collisions.翻译：
使用随意一个哈希函数
$h$ ,把 n 个keys存到$m = n^2$ 个slot里，有冲突的概率小于$1/2$
题目来自Homework 8
Implement a hash for text.
Given a string as input, construct a hash with words as keys, and wordcounts as values. Your implementation should include:
• a hash function that has good properties for text
• storage and collision management using linked lists
• operations: insert(key,value), delete(key), increase(key), find(key), list-all-keys
先来找一个适合string的hash func，google了以后：
http://www.cse.yorku.ca/~oz/hash.html
实施
复习一下：
Python
ord:输入一个字符，返回ASCII数值
hex：输入整数，返回16进制
python 位运算：
按位运算符是把数字看作二进制来进行计算的。Python中的按位运算法则如下：
下表中变量 a 为 60，b 为 13，二进制格式如下：
a = 0011 1100
b = 0000 1101
-----------------
a&b = 0000 1100
a|b = 0011 1101
a^b = 0011 0001
~a = 1100 0011
实施hash_djb2:
def hash_djb2(s):
hash = 5381
for x in s:
hash = (( hash << 5) + hash) + ord(x)
return hash & 0xFFFFFFFF这个函数的magic在于他的两个魔法数字：33和5381，这里用的是5381；
贴一点test case:
print(hash_djb2(u'hello world')) # '0xa6bd702fL'
print(hash_djb2('a'))
print(hash_djb2('b'))
#输出：
894552257
177670
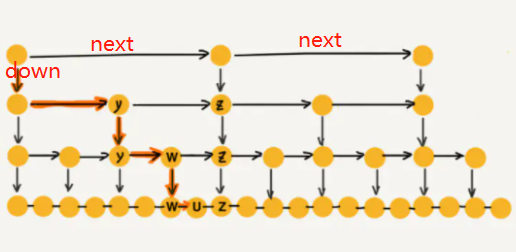
177671跳表在工业中也会被经常用到，墙裂建议阅读下文：
https://www.jianshu.com/p/9d8296562806
简单概括重点：
跳表的索引高度
假如原始链表包含 n 个元素，则一级索引元素个数为 n/2、二级索引元素个数为 n/4、三级索引元素个数为 n/8 以此类推。所以，索引节点的总和是：n/2 + n/4 + n/8 + … + 8 + 4 + 2 = n-2，空间复杂度是 O(n)。
为什么Redis选择使用跳表而不是红黑树来实现有序集合？
Redis 中的有序集合(zset) 支持的操作：
- 插入一个元素
- 删除一个元素
- 查找一个元素
- 有序输出所有元素
- 按照范围区间查找元素（比如查找值在 [100, 356] 之间的数据）
其中，前四个操作红黑树也可以完成，且时间复杂度跟跳表是一样的。但是，按照区间来查找数据这个操作，红黑树的效率没有跳表高。按照区间查找数据时，跳表可以做到 O(logn) 的时间复杂度定位区间的起点，然后在原始链表中顺序往后遍历就可以了，非常高效。
跳表Skiplist的Python实现。
https://leetcode.com/problems/design-skiplist/discuss/?currentPage=1&orderBy=most_votes&query=
Python:
这个实现是我从leetcode某个大哥那抄过来的，有做改动；
It really took me one day to understand....
class Node:
def __init__(self, val):
self.val = val
self.next = None
self.down = None
next 指的是相同级别的下一个元素，就是往右走；
down 指的是下一个级别的相同元素，就是往下走；
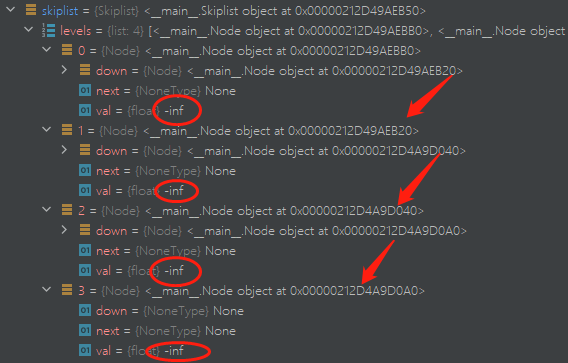
初始化：
class Skiplist:
def __init__(self):
self.levels = []
self.max_level = 4
prev = None
for i in range(self.max_level):
node = Node(-math.inf)
self.levels.append(node)
if prev:
prev.down = node
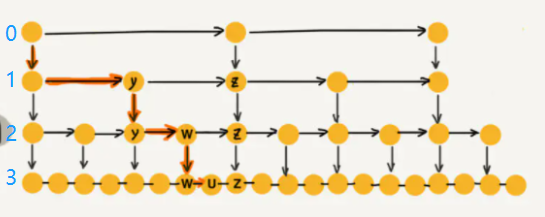
prev = node在这次的实现中，levels储存的是每个级别的单链表。
index = 0 的位置存的是最高级的链表，我们在这一级别实现skip 操作；
index = 3 存的是最基础的链表，也就是长度为
后面统一一下口径，最高级的链表指 index = 0, 元素最少的那一条链表；
通过上述代码，你实现了如下的操作：
self.level中储存了每个级别的对应的链表, 每个级别链表的初始化都为负无穷：-math.inf- 让每个更高级的链表对象指向更基础的级别；
如图：
实现iter
def _iter(self, val):
res = []
l = self.levels[0]
while l:
while l.next and l.next.val < val:
l = l.next
res.append(l)
l = l.down
return res这个函数是很核心的函数，后面的操作都会用到它；
这个函数实现了skip的作用：
-
输入一个
val, 只要下一个元素比val小，就往右走(next)； -
否则，就往下走(
down)；
为什么是while l,因为他只能往右或者往下走，就一定有走到None的时候；
所以，这个函数中返回的结果res是每个级别中刚好小于val的那个node节点对象；
即使下一个元素能等于val, 也停留在之前一个，方便后续delete操作；
这个函数实现了，理解了返回的res是什么，后续就简单了；
search 搜索操作：
def search(self, target: int) -> bool:
last = self._iter(target)[-1]
return last.next and last.next.val == target上一个_iter函数停留在输入值的前一个数，所以直接检查下一个元素就好了；
add/insert操作
def add(self, num: int) -> None:
res = self._iter(num)
prev = None
for i in range(len(res) - 1, -1, -1):
node = Node(num)
#res[i]是刚好比val小的元素，那么next就比val大咯
node.next = res[i].next
#指向低级链表
node.down = prev
#res[i]是刚好比val小的元素
res[i].next = node
prev = node
rand = random.random()
if rand > 0.5:
break- 这个
for是从低级走到高级的 - 在保证了基础级别存在插入的数值以后，每个更高级的节点都
random一次，大于0.5就在更高级的节点添加该节点；
erase/delete删除操作
有了_iter操作后很简单，不用说了
先仔细阅读下原文：
A red-black tree is a binary search tree with one extra bit of storage per node: its
color, which can be either RED or BLACK. By constraining the node colors on any
simple path from the root to a leaf, red-black trees ensure that no such path is more
than twice as long as any other, so that the tree is approximately balanced.
Each node of the tree now contains the attributes
color,key,left,right, andp.
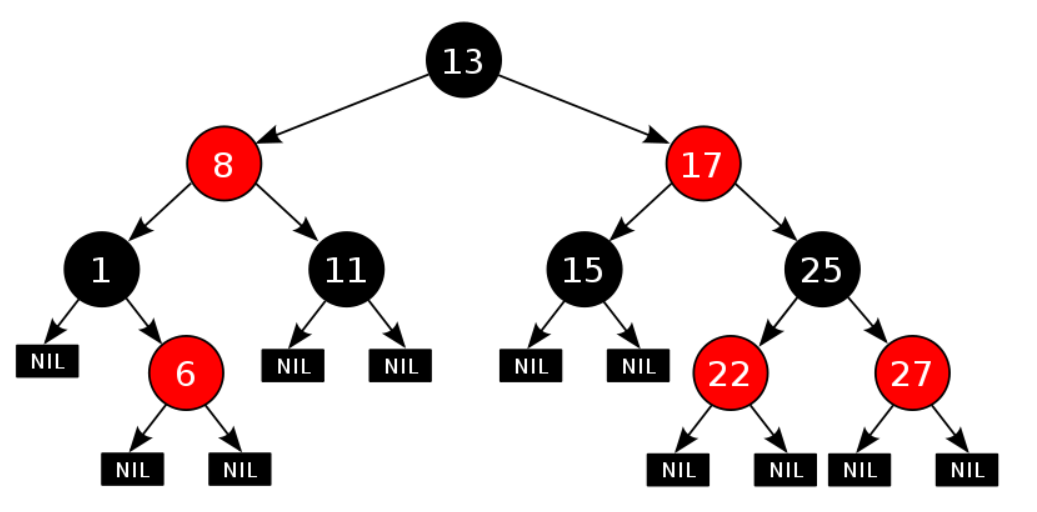
所以红黑树本质就是自平衡的BST，但是他多了颜色属性，并且服从红黑树性质:
1）每个结点要么是红的，要么是黑的。
2）根结点是黑的。
3）每个叶结点（叶结点即指树尾端NIL指针或NULL结点）是黑的。
4）如果一个结点是红的，那么它的俩个儿子都是黑的。
5）对于任一结点而言，其到叶结点树尾端NIL指针的每一条路径都包含相同数目的黑结点。
红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。
如果忘记了BST的性质，先去上面复习一下 Insertion 和 Deletion 的操作。
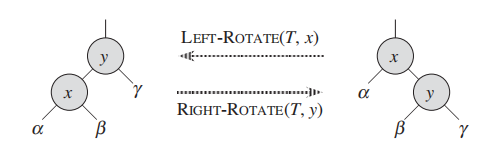
When we do a left rotation on a node x, we assume that its right child y is not T:nil; x may be any node
in the tree whose right child is not T:nil. The left rotation “pivots” around the link
from x to y. It makes y the new root of the subtree, with x as y’s left child and y’s
left child as x’s right child.
我们要左旋节点某子树的根节点： x;
假设x 的右child y的 不为空：
旋转围绕着 x和y的连接，我们让：
- ``y``成为该子树的root,
- ``x``成为 ``y`` 的左child, ``y`` 原来的左child成为 ``x``的右child。
figure 来自原文13.2 p313
伪码：
左旋、右旋的时间复杂度为**$O(1)$**。
插入的时间复杂度为
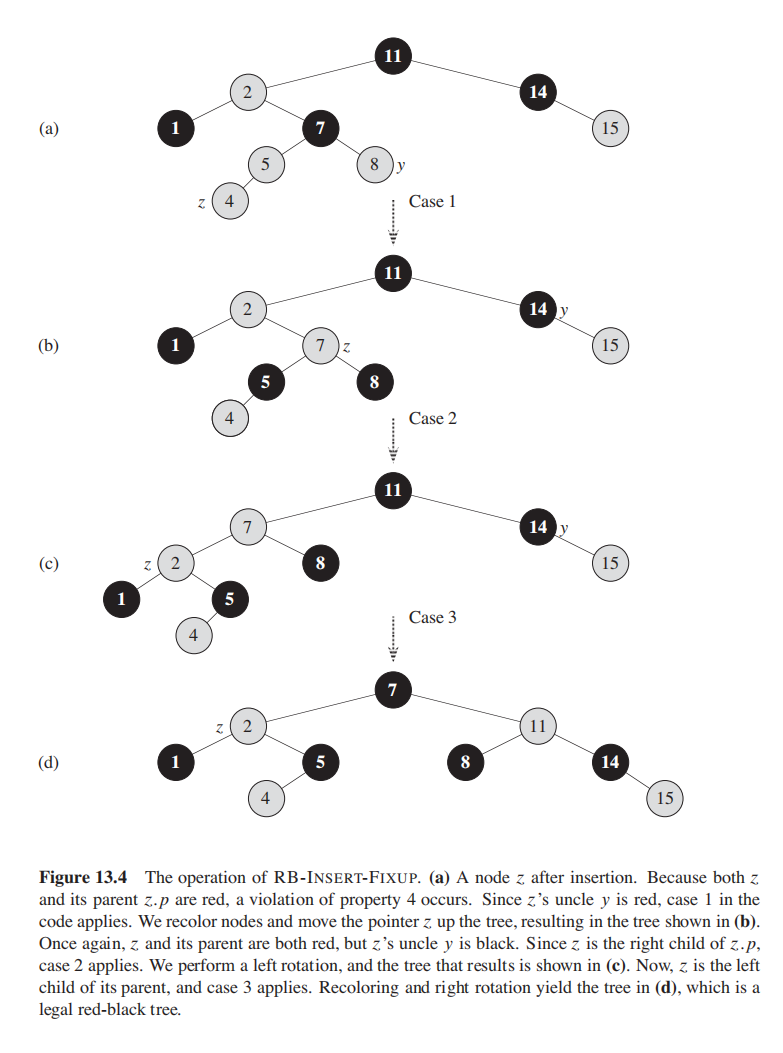
为了保证红黑树性质，需要一个额外的fix函数来 recolor 以及 rotate
今天被旋晕了，下次再来吧
Case 1: z's uncle y is red
Case 2: z’s uncle y is black and z is a right child
Case 3: z’s uncle y is black and z is a left child
插入以后会导致RBT的那些性质会被violated?
- Property 2: 根节点是黑
当树为空时，插入的节点是红色的，这时违反；
- Property 4: 红色节点不能有红色节点，只能有两个黑色节点；（NIL也算黑色）
https://www.quora.com/Difference-between-binary-search-tree-and-red-black-tree
一开始没理解R-B-Tree 比 BST强的地方，谷歌了一下总结如下：
常规的BST不是self-balancing的，因此你的插入顺序会导致其他操作的时间复杂度发生变化；
比如：
- if you inserted in order {2, 3, 1}, the BST will be O( log(N) )
- however if you inserted {1,2,3}, the BST will be O( N ), like a linked list.
而RB-Tree总能自平衡，来确保你的操作总会是$O(lgn)$。
Red Black Tree : best case O(logN), worst case O(logN) Binary Search Tree: best case O(logN), worst case O(N)
egg_drop