Skip to content

Latest commit

 

History

History
192 lines (156 loc) · 9.16 KB

README.md

File metadata and controls

192 lines (156 loc) · 9.16 KB
Raw

Packing

InvertedTomato.Packing is all about encoding data in the smallest possible way quickly. This is super useful for both storage and transmission of data when size and speed are both important. Data isn't compressed, at least not in the traditional sense, rather stored in encoded in efficently manners.

TLDR

Here's how to squash 24 bytes of data down to 2 using Fibonacci coding:

using InvertedTomato.Packing;
using InvertedTomato.Packing.Codecs.Integers;

// Encode some values...
using var stream = new MemoryStream(); // Could be a FileStream or a NetworkStream
using (var writer = new StreamBitWriter(stream))
{
    // Pick a codec - you can use one or many - so long as you decode in the same order you encoded
    var fib = new FibonacciIntegerEncoder(writer);

    // Encode some values using the Fibonacci codec
    fib.EncodeUInt64(1);
    fib.EncodeUInt64(2);
    fib.EncodeUInt64(3);
}

Console.WriteLine("Compressed data is " + stream.Length + " bytes"); // Output: Now data is 2 bytes

// Decode the values...
stream.Position = 0;
using (var reader = new StreamBitReader(stream))
{
    var fib = new FibonacciIntegerDecoder(reader);

    // Decode the Fibonacci values
    Console.WriteLine(fib.DecodeUInt64()); // Output: 1
    Console.WriteLine(fib.DecodeUInt64()); // Output: 2
    Console.WriteLine(fib.DecodeUInt64()); // Output: 3
}

Introduction

Modern PCs have stacks of RAM, so it's usually not a problem that integers take 4-8 bytes each to store in memory. There are times however when this is a problem. For exammple:

  • When you want to store a large set of numbers in memory (100 million * 8 bytes = 760MB)
  • When you want to store a large set of numbers on disk
  • When you want to transmit numbers over a network (the Internet?) quickly

In almost all cases those numbers can be stored in a much lower number of bytes. Heck, its possible to store three integers in a single byte.

Algorithms

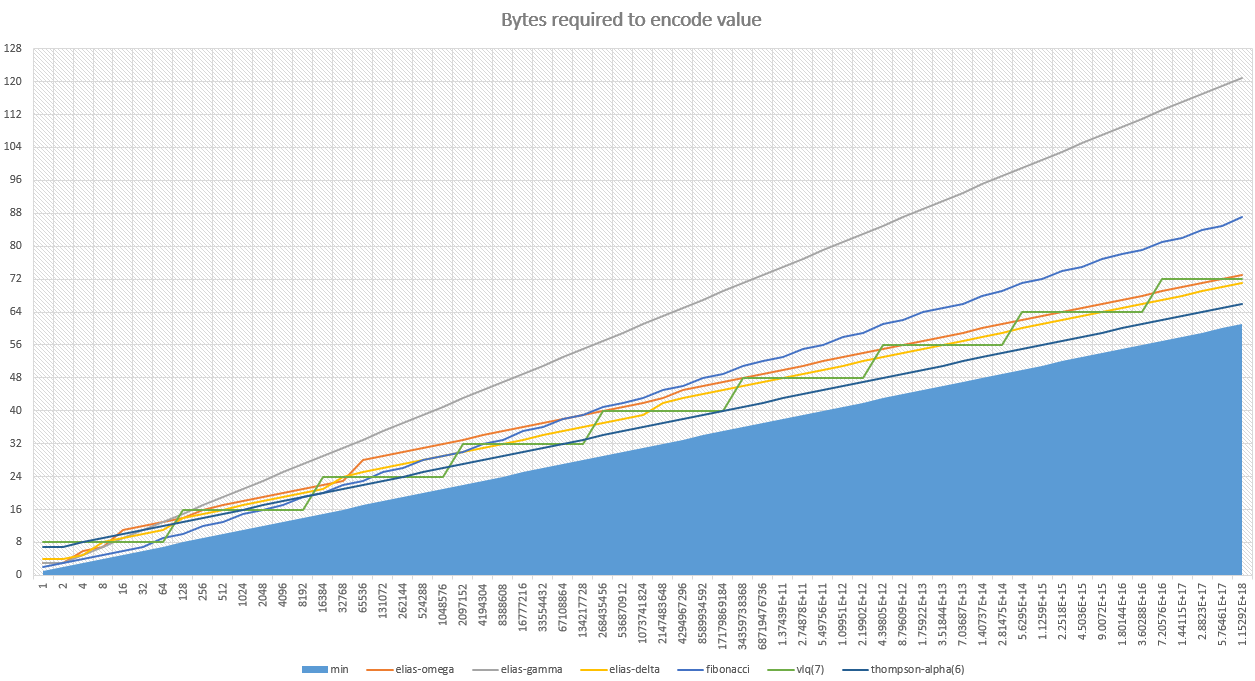
The example in the TLDR section used the Fibonacci codec. Whilst this codec is excellent for small numbers, it's not so great when numbers get larger. You really need to select a codec with your domain in mind. Following is a summary of the codecs available, their strengths and weaknesses.

Bits required to represent each number with each codec

Keep in mind that there is a physical minimum possible size for each number. That is displayed in blue. alt text

Fibonacci (best for integers <8,000)

  • Family: universal code
  • Random access: yes (can jump ahead)
  • Lossy: no (doesn't approximate)
  • Universal: yes (can handle any number)
  • Details: Wikipedia
  • Options:

This is a very interesting algorithm - it encodes the numbers against a Fibonacci sequence. It's the best algorithm in the pack for numbers up to 8,000, It degrades after that point - but not horrendously so. This is my personal favorite algo.

Thompson-Alpha (best for integers >8,000)

  • Family: none
  • Random access: no
  • Universal: no (can only handle a predefined range of numbers)
  • Details: N/A
  • Options:
    • Length bits

I couldn't find an algorithm which performed well for large integers (>8,000), so this is my own. In it's default configuration it has a flat 6-bits of overhead for each integer, no matter it's size. That makes it excellent if your numbers have a large distribution.

Variable Length Quantities (VLQ)

  • Random access: no (can't jump ahead)
  • Universal: yes (can handle any number)
  • Details: Wikipedia
  • Options:

It seems VLQ was originally invented by the designers of MIDI (you know, the old-school MP3). The algorithm is really retro, there's stacks of variations of it's spec and it smells a little musty, but it's awesome! It produces pretty good results for all numbers with a very low CPU overhead.

Inverted Variable Length Quantities (VLQ)

  • Random access: no (can't jump ahead)
  • Universal: yes (can handle any number)
  • Details: N/A
  • Options:

Similar to VLQ, Inverted-VLQ is a slight variation which uses a final-byte flag, rather than a more-bit flag. Theoretically this has slightly better CPU performance for numbers that encode to more than three bytes.

Elias-Omega

  • Family: universal code
  • Random access: no (can't jump ahead)
  • Universal: yes (can handle any number)
  • Supported values: all
  • Details: Wikipedia

Elias Omega is a sexy algorithm. It's well thought out and utterly brilliant. But I wouldn't use it. It does well for tiny integers (under 8), but just doesn't cut the mustard for larger values - all other algorithms do better. Sorry Omega :-/.

Elias-Gamma

  • Family: universal code
  • Random access: no (can't jump ahead)
  • Universal: yes (can handle any number)
  • Supported values: all
  • Details: Wikipedia

Like Elias-Omega, this is a very interesting algorithm. However it's only really useful for small integers (less than 8). For bigger numbers it performs terribly.

Elias-Delta

  • Family: universal code
  • Random access: no (can't jump ahead)
  • Universal: yes (can handle any number)
  • Supported values: all
  • Details: Wikipedia

I have a lot of respect for this algorithm. It's an all-rounder, doing well on small numbers and large alike. If you knew you were mostly going to have small numbers, but you'd have a some larger ones as well, this would be my choice if it weren't for ThompsonAlpha. The algorithm is a little complex, so you might be cautious if you have extreme CPU limitations.

Comparing algorithms

In order to make an accurate assessment of a codec for your purpose, some algorithms have a method CalculateEncodedBits that allows you to know how many bits a given value would consume when encoded. I recommend getting a set of your data and running it through the CalculateEncodedBits methods of a few algorithms to see which one is best.

Signed and unsigned

If your numbers are unsigned (eg, no negatives), be sure to use unsigned calls to the Codec. That way you'll get the best size reduction. Obviously fall back to signed if you must. Hand-waving, it'll cost you an extra bit or so for each value if you used signed.

Even better reduction

There are a few techniques you can use to further increase the reduction of your integers. Following is a summary of each

Use deltas

Smaller numbers use less space. So take a moment to consider what you can do to keep your numbers small. One common technique is to store the difference between numbers instead of the numbers themselves. Consider if you wanted to store the following sequence:

  • 10000
  • 10001
  • 10002
  • 10003
  • 10004

If you converted them to deltas you could instead store:

  • 1000
  • 1
  • 2
  • 3
  • 4

This sequence uses a stack less bytes!

Naturally this isn't suitable for all contexts. If the receiver has the potential to loose state (eg. UDP transport) you'll have to include a recovery mechanism (eg keyframes), otherwise those deltas become meaningless.

Make lossy

Sometimes it's okay to loose data when encoding. Let's say that you're compressing a list of distances in meters, however you only really care about the distance rounded to the nearest 100 meters. You can save a heap of data by dividing your value by 100 before compressing it, and multiplying it by 100 after.

Use a false floor

Sometimes all of your values are always going to be above zero. Let's say that you're storing the number of cars going over a busy bridge each hour. If it's safe to assume there will never be 0 cars you could save some data by subtracting one from your value before encoding and adding one after decoding.

This may seem like a trivial optimization, however with most algorithms it will save you one or two bits per number. If you have several million numbers that really adds up.

Intermix codecs

So Fibonacci is best for small numbers, and ThompsonAlpha is better for large values - so why not use both? So long as I read it in the same order I wrote it. If you use this cleverly you can get some real size wins.

Compress it

You thought we were compressing integers already? We'll it depends how you define your terms, but I'd say I was just encoding them more cleverly. But you can compress it as well. Check out BrotliStream. If you wrap your stream in this you can further compress your dataset. While the above encoding stores your data in the most efficent manner, Brotli will then look for patterns in your data to exploit to make it smaller again.