对于贪心,大多数同学都会感觉,不就是常识嘛,这算啥算法,那么本周的题目就可以带大家初步领略一下贪心的巧妙,贪心算法往往妙的出其不意。
在贪心算法:加油站中给出每一个加油站的汽油和开到这个加油站的消耗,问汽车能不能开一圈。
这道题目咋眼一看,感觉是一道模拟题,模拟一下汽车从每一个节点出发看看能不能开一圈,时间复杂度是O(n^2)。
即使用模拟这种情况,也挺考察代码技巧的。
for循环适合模拟从头到尾的遍历,而while循环适合模拟环形遍历,对于本题的场景要善于使用while!
如果代码功力不到位,就模拟这种情况,可能写的也会很费劲。
本题的贪心解法,我给出两种解法。
对于解法一,其实我并不认为这是贪心,因为没有找出局部最优,而是直接从全局最优的角度上思考问题,但思路很巧妙,值得学习一下。
对于解法二,贪心的局部最优:当前累加rest[j]的和curSum一旦小于0,起始位置至少要是j+1,因为从j开始一定不行。全局最优:找到可以跑一圈的起始位置。
这里是可以从局部最优推出全局最优的,想不出反例,那就试试贪心。
解法二就体现出贪心的精髓,同时大家也会发现,虽然贪心是常识,有些常识并不容易,甚至很难!
在贪心算法:分发糖果中我们第一次接触了需要考虑两个维度的情况。
例如这道题,是先考虑左边呢,还是考虑右边呢?
先考虑哪一边都可以! 就别两边一起考虑,那样就把自己陷进去了。
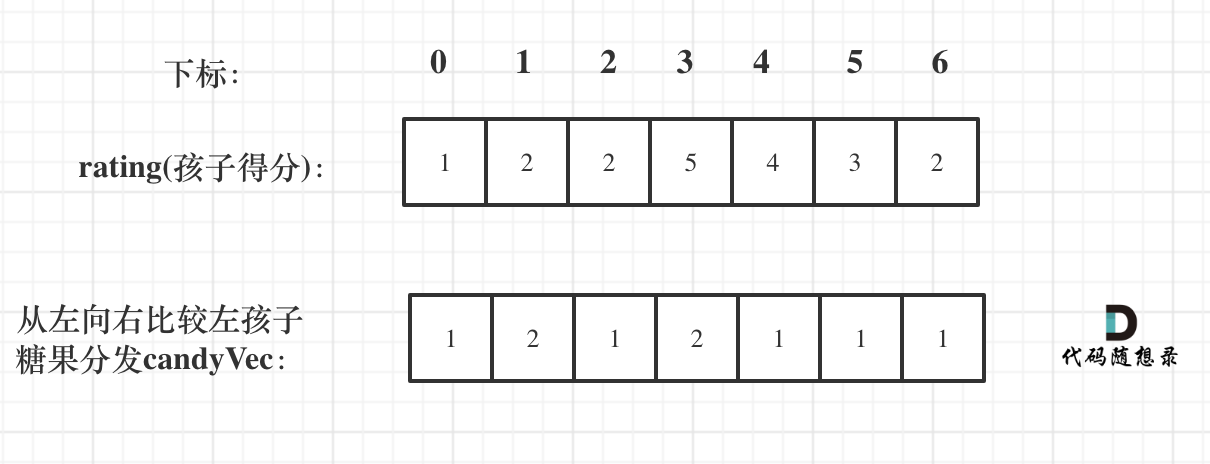
先贪心一边,局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果
如图:
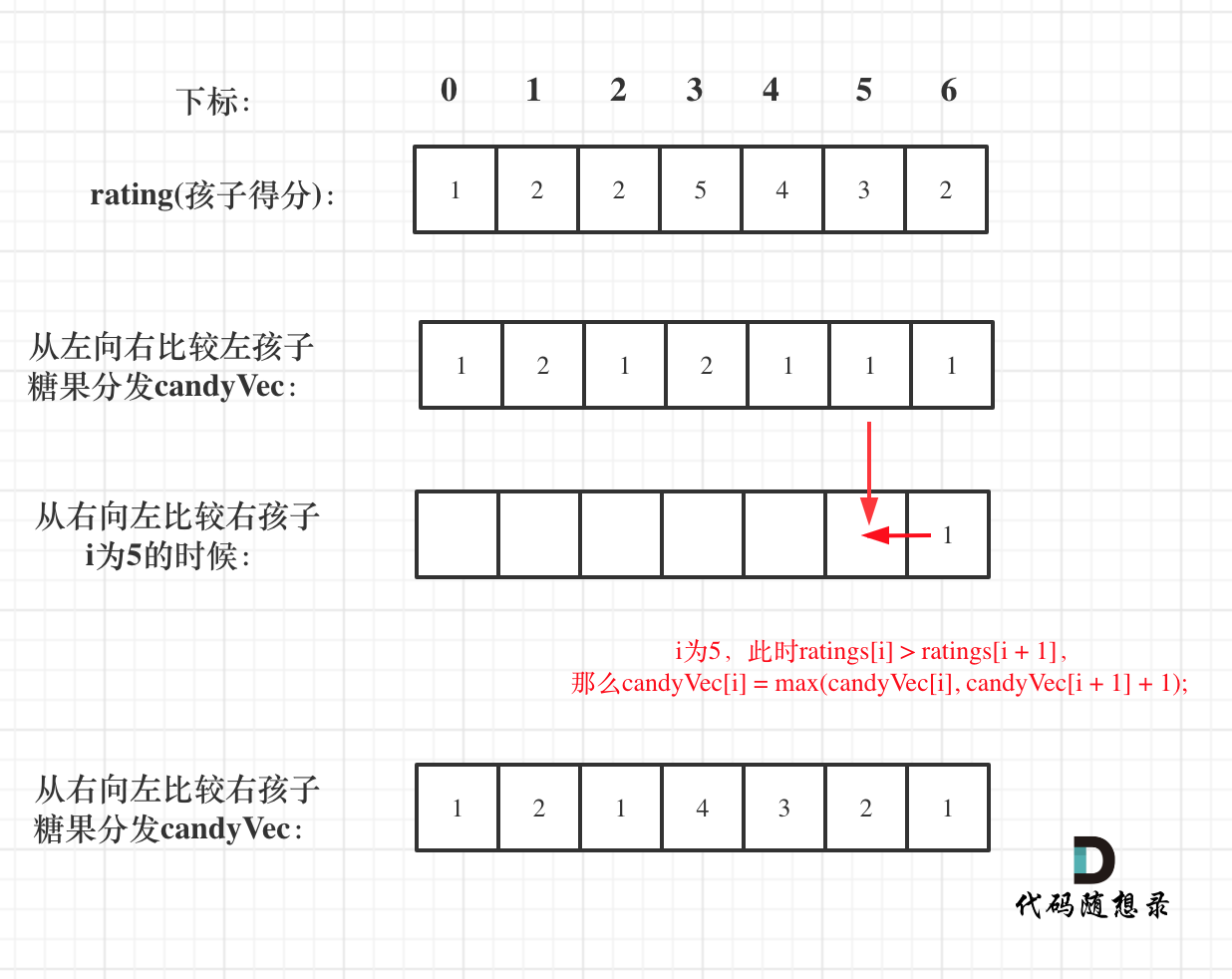
接着在贪心另一边,左孩子大于右孩子,左孩子的糖果就要比右孩子多。
此时candyVec[i](第i个小孩的糖果数量,左孩子)就有两个选择了,一个是candyVec[i + 1] + 1(从右孩子这个加1得到的糖果数量),一个是candyVec[i](之前比较右孩子大于左孩子得到的糖果数量)。
那么第二次贪心的局部最优:取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,保证第i个小孩的糖果数量即大于左边的也大于右边的。全局最优:相邻的孩子中,评分高的孩子获得更多的糖果。
局部最优可以推出全局最优。
在贪心算法:柠檬水找零中我们模拟了买柠檬水找零的过程。
这道题目刚一看,可能会有点懵,这要怎么找零才能保证完整全部账单的找零呢?
但仔细一琢磨就会发现,可供我们做判断的空间非常少!
美元10只能给账单20找零,而美元5可以给账单10和账单20找零,美元5更万能!
局部最优:遇到账单20,优先消耗美元10,完成本次找零。全局最优:完成全部账单的找零。
局部最优可以推出全局最优。
所以把能遇到的情况分析一下,只要分析到具体情况了,一下子就豁然开朗了。
这道题目其实是一道简单题,但如果一开始就想从整体上寻找找零方案,就会把自己陷进去,各种情况一交叉,只会越想越复杂了。
在贪心算法:根据身高重建队列中,我们再一次遇到了需要考虑两个维度的情况。
之前我们已经做过一道类似的了就是贪心算法:分发糖果,但本题比分发糖果难不少!
贪心算法:根据身高重建队列中依然是要确定一边,然后在考虑另一边,两边一起考虑一定会蒙圈。
那么本题先确定k还是先确定h呢,也就是究竟先按h排序呢,还先按照k排序呢?
这里其实很考察大家的思考过程,如果按照k来从小到大排序,排完之后,会发现k的排列并不符合条件,身高也不符合条件,两个维度哪一个都没确定下来。
所以先从大到小按照h排个序,再来贪心k。
此时局部最优:优先按身高高的people的k来插入。插入操作过后的people满足队列属性。全局最优:最后都做完插入操作,整个队列满足题目队列属性。
局部最优可以推出全局最优,找不出反例,那么就来贪心。
「代码随想录」里已经讲了十一道贪心题目了,大家可以发现在每一道题目的讲解中,我都是把什么是局部最优,和什么是全局最优说清楚。
虽然有时候感觉贪心就是常识,但如果真正是常识性的题目,其实是模拟题,就不是贪心算法了!例如贪心算法:加油站中的贪心方法一,其实我就认为不是贪心算法,而是直接从全局最优的角度上来模拟,因为方法里没有体现局部最优的过程。
而且大家也会发现,贪心并没有想象中的那么简单,贪心往往妙的出其不意,触不及防!