00-ORB-SLAM3基础知识点.md

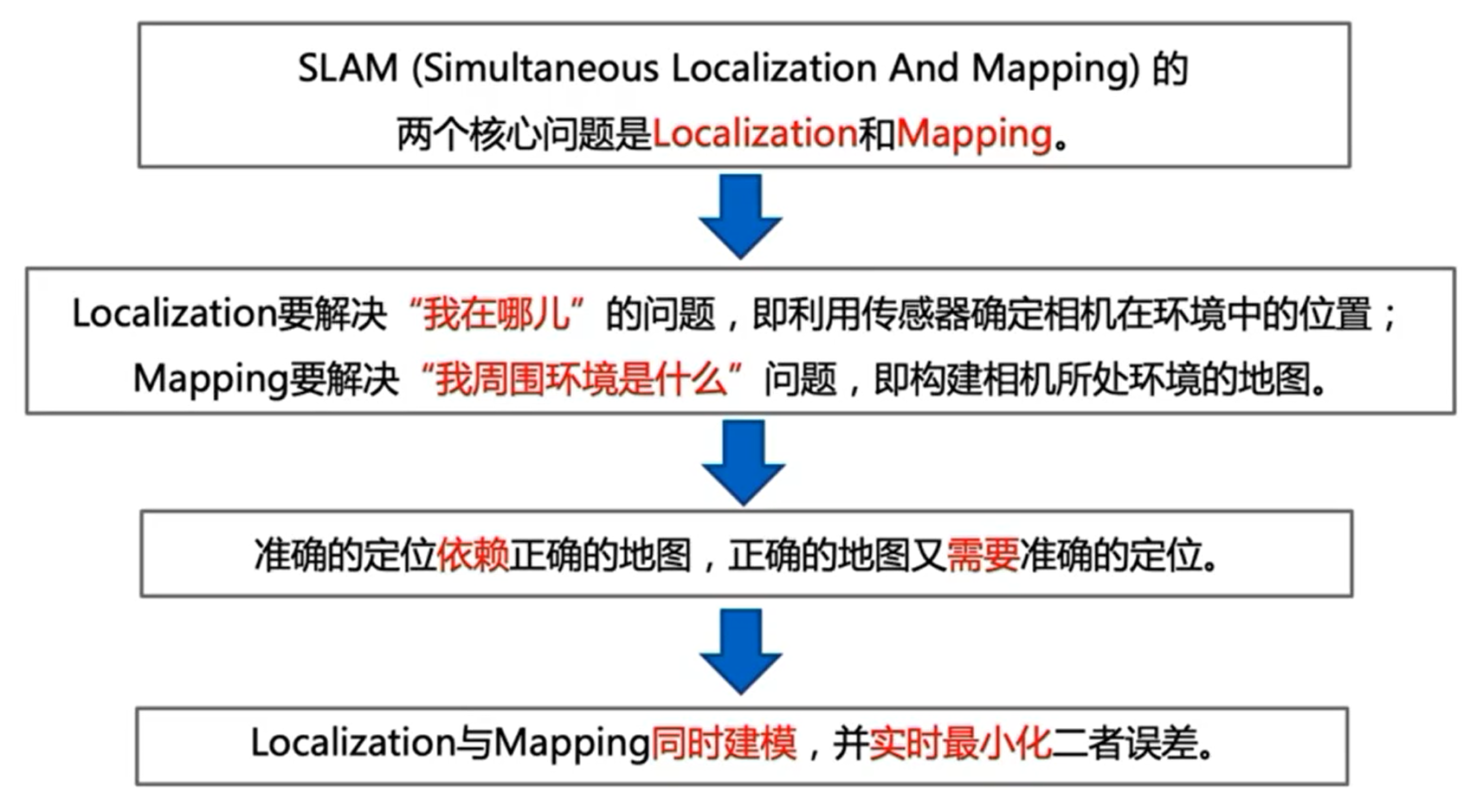
原始 Markdown文档、Visio流程图、XMind思维导图见：https://github.com/LiZhengXiao99/Navigation-Learning

[TOC]

1、视觉SLAM简介

1. 定位与建图关系

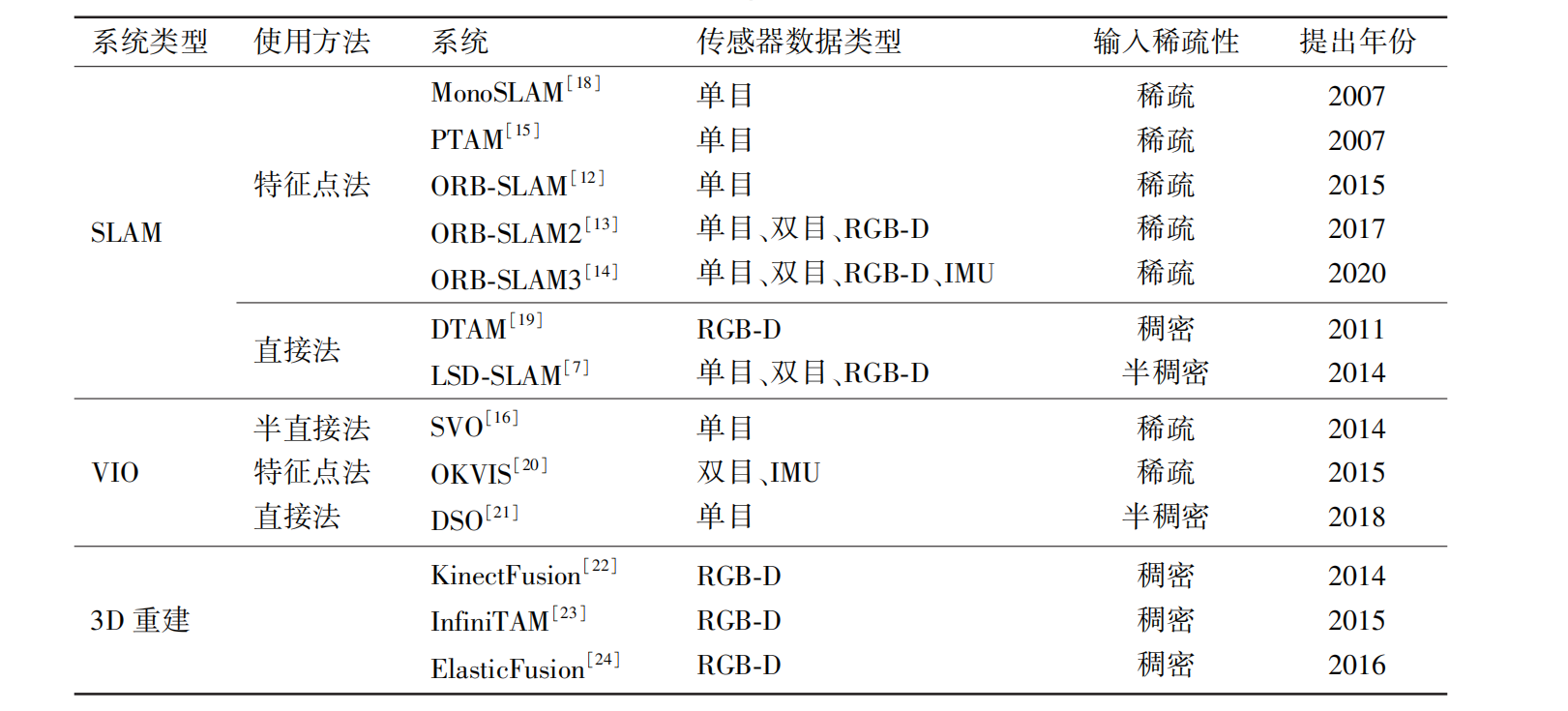
代表性 SLAM 系统包括：

2. 单目、双目、RGB-D

• 单目相机：单目相机在环境中移动，不断获得图像帧，通过两帧之间三角化计算，将空间的点投影到相机空间，对环境进行建模。
• 双目相机：左右相机同时能得到两图像帧，直接可以获得距离。
• RGB-D相机：实现方式有多种：
  • Kinect1：使用红外光，根据返回结构光图像，计算距离。
  • Kinect2：用脉冲信号，根据收发信号时间差计算距离。

3. 特征点法、直接法

• 特征点法：处理的是特征点，先提取图像特征，通过特征匹配估计相机运动，优化的是重投影误差，常见开源方案有 ORB-SLAM。
• 直接法：处理的是像素，根据像素灰度信息估计相机的运动，可以不用计算关键点和描述子，优化的是光度误差；根据使用的像素数量可以分为稀疏、半稠密和稠密三种，常见的开源方案有 LSD-SLAM、DSO 等。

4. SLAM 框架

当前主流的 SLAM 系统由 4 个阶段组成，分别为前端视觉里程计(visual odometry, VO)、后端优化(optimization)、回环检测( loop closing) 和三维地图建立(mapping)。

• 视觉里程计（Visual Odometry，VO）：估算相邻图像间相机的运动，以及局部地图，求解传感器在各个时刻的位置信息。也称前端（Front END）。
• 后端优化（Optimization）：接收不同时刻视觉里程计测量的相机位姿，以及回环检测的信息，根据它们进行优化，得到全局一致的轨迹和地图。也称后端（Back End）。
• 回环检测（Loop Closing）：判断出载体是否到达过先前的位置，如果检测到就将数据传给后端。
• 建图（Mapping）：根据估计的轨迹，建立与任务要求对应的地图。

2、ORB 图像特征

ORB 特征包括特征点和描述子：

• 特征点：可以理解为图像中比较显著的点，如轮廓点、暗区的亮点、亮区的暗点等，采用 FAST 得到。
• 描述子：获得特征点后，要以某种方式描述特征点的属性，这些属性的描述称之为该特征点的描述子，采用 BRIEF 得到。

1. FAST

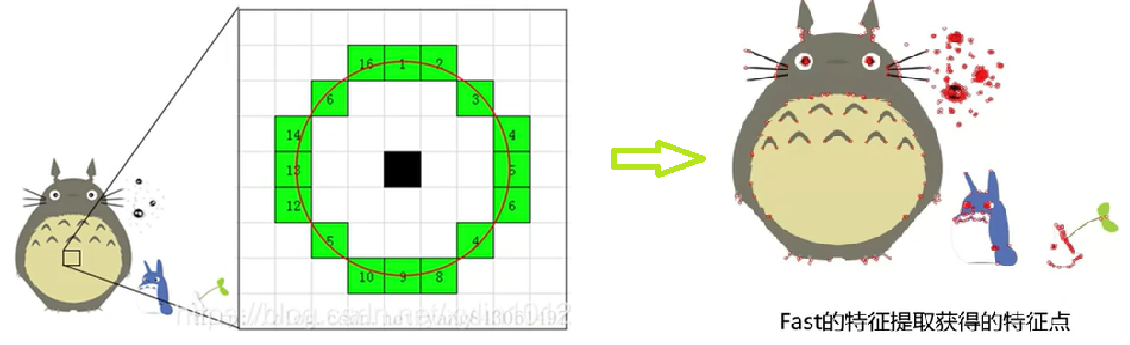
FAST 核心思想就是找出哪些有代表的点，即拿一个点与周围的点比较，如果和周围大部分点都不一样（有明显的像素值变化）就可以认为是一个特征点。

FAST 的计算过程，即逐个判断像素是否为特征点：

• 设定一个合适的阙值 $\mathrm{t}$：当 2 个点的灰度值之差的绝对值大于 $\mathrm{t}$ 时，则认为这 2 个点不相同。
• 考虑该像素点周围的 16 个像素。如果这 16 个点中有连续的 $n$ 个点 都和点不同，那么它就是一个角点。这里 n 设定为 12。
• 现在提出一个高效的测试，来快速排除一大部分非特征点的点。 该测试仅仅检查在位置 1、9、5 和 13 四个位置的像素。如果是一个角点，那么上述四个像素点中至少有 3 个应该和点相同。如果都不满足，那么不可能是一个角点。

2. BRIEFF

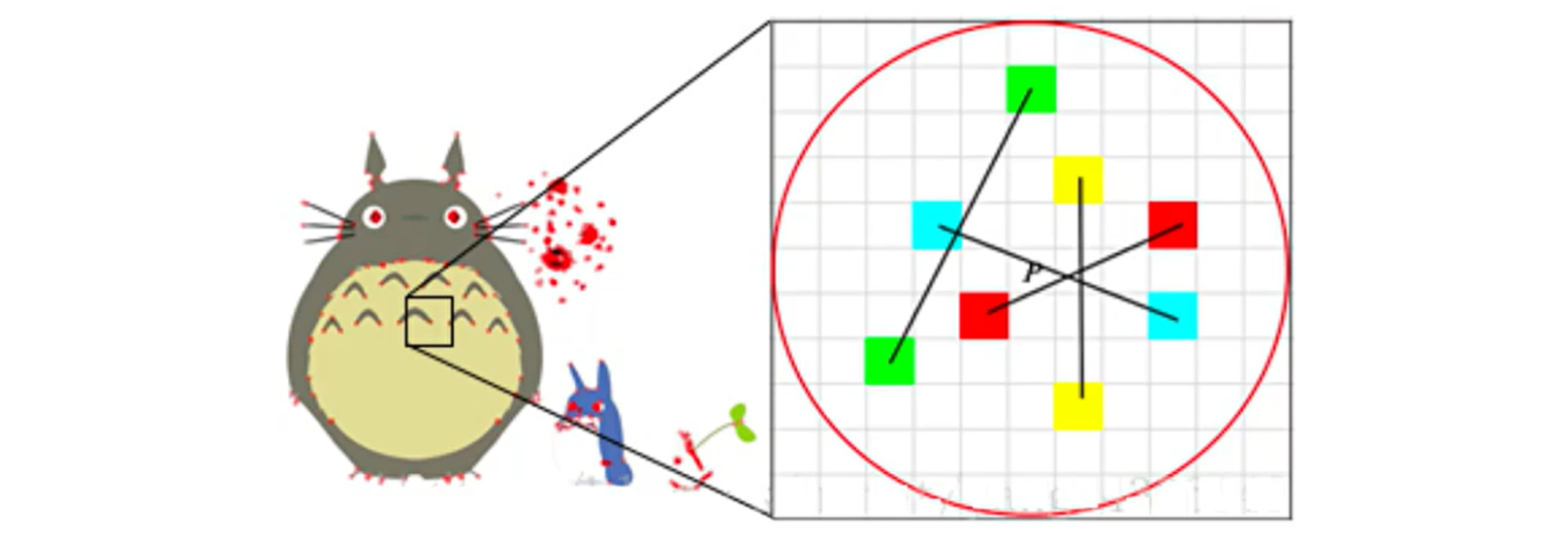
BIREF 算法的核心思想是在关键点 P 的周围以一定模式选取 N 个点对，把这 N 个点对的比较结果组合起来作为描述子。

BIREF 算法计算流程：

• 以关键点 $P$ 为原点，以 $d$ 为半径作圆 $O$。

• 在圆 $O$ 内某一模式选取 $N$ 个点对。这里为方便说明，$N=4$，实际应用中 $N$ 可以取 512 。

• 假设当前选取4个点，分别标记为：$P_{1}(A, B) , P_{2}(A, B) ,P_{3}(A, B) , P_{4}(A, B)$。

• 定义操作 T：$ T(P(A, B))=\left{\begin{array}{ll}1 & I_{A} \ 0 & I_{B}\end{array}\right.$，其中 $I_A$ 表示 $A$ 的灰度。

• 分别对已选取的点进行 T 操作，将获得的结果进行组合。比如： $$ \begin{array}{ll} T\left(P_{1}(A, B)\right)=1 & T\left(P_{2}(A, B)\right)=0 \ T\left(P_{3}(A, B)\right)=1 & T\left(P_{4}(A, B)\right)=1 \end{array} $$

• 则最终描述子为：1011

3. ORB 改进 BRIEF

实际情况下，从不同的距离，不同的方向、角度，不同的光照条件下观察一个物体时，物体的大小，形状 ，明暗都会有所不同。但我们的大脑依然可以判断它是同一件物体。

理想的特征描述子应该具备这些性质。即，在大小、 方向、明暗不同的图像中，同一特征点应具有足够相似的描述子，称之为描述子的可复现性。

当以某种理想的方式分别计算上图中红色点的描述子时，应该得出同样的结果。即描述子应该对光照 (亮度) 不敏感，具备尺度一致性（大小），旋转一致性 (角度) 等。

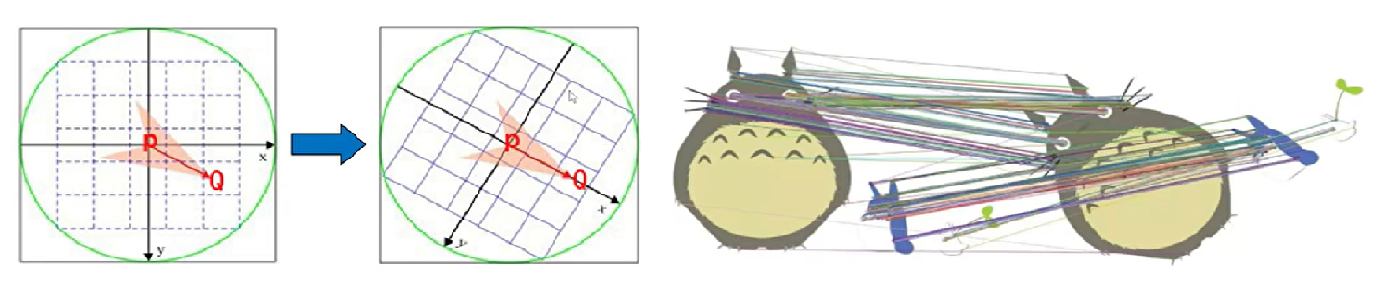
当图像发生旋转时，用上面方法计算得到的描述子显然会改变，缺乏旋转一致性。ORB 在计算 BRIEF 描述子时建立的坐标系以关键点为圆心，以关键点和选取区域质心（灰度值加权中心）的连线为 X 轴建立二维坐标系。如下图：PQ 作为坐标轴，在不同旋转角度下，同样的几个特征点的描述子是不变的，就解决了旋转一致性问题。

4. 特征匹配

例如，特征点 A、B 的描述子分别是：10101011、10101010。首先设定一个阈值，比如 85%，当 A、B 的描述子相似程度大于 85% 时，认为是相同特征点。该例中相似度 87.5%，A、B 是匹配的。

3、图像关键帧

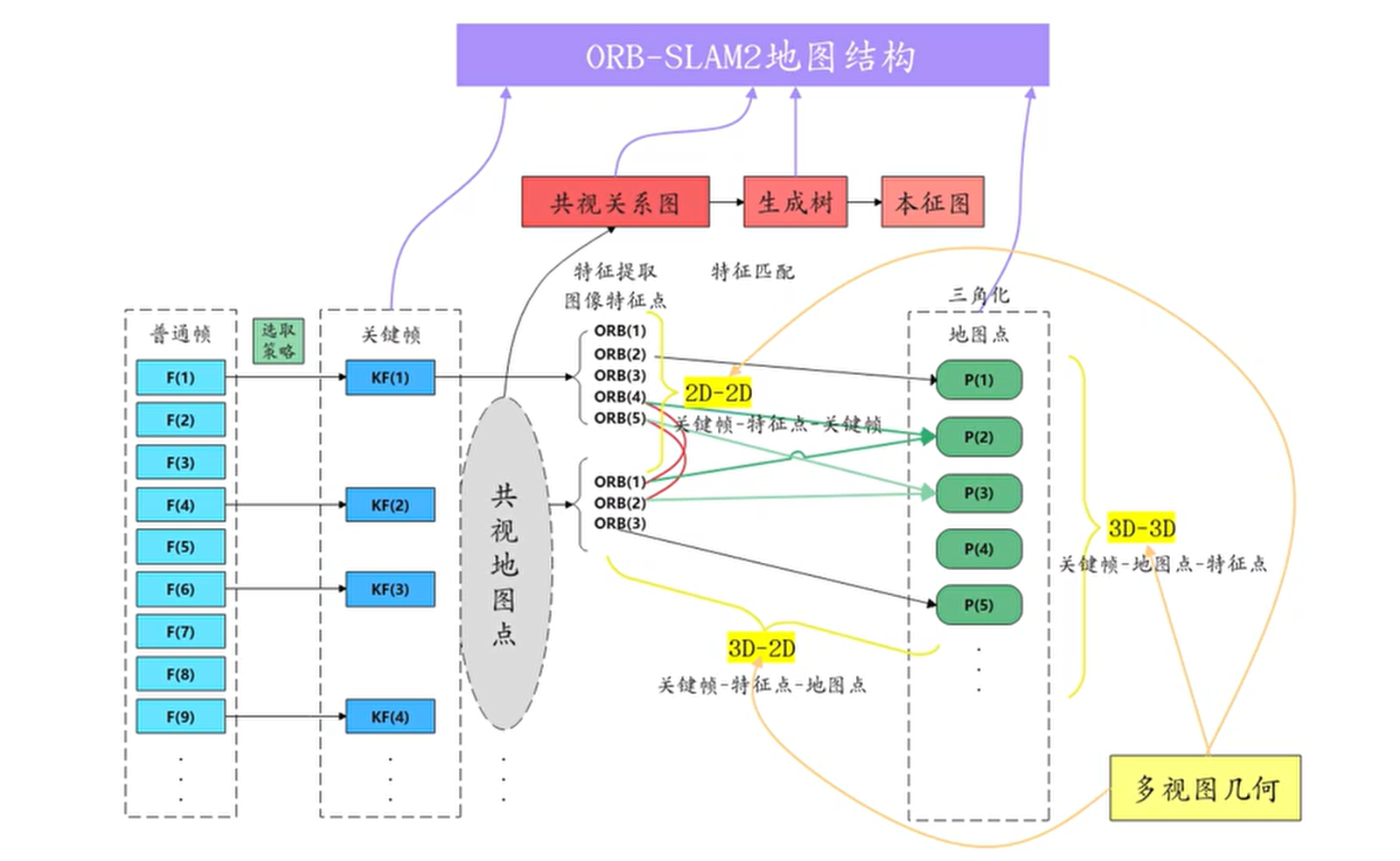
关键帧是图像帧中具有代表性的帧，目的在于降低信息冗余度、减少计算机资源的消耗、保证系统的实时性。

1. 关键帧的选取原则

• 图像质量：画面清晰、特征点多、分布均匀。
• 连接关系：与其它关键帧直接有一定的共视关系，同时重复度也不能太高。

2. 共视

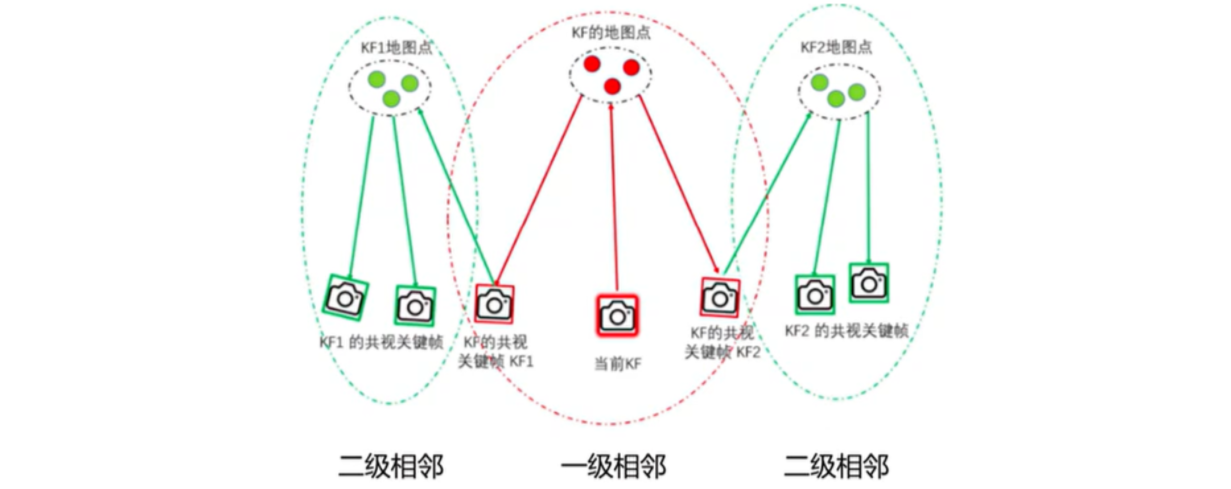
• 共视关键帧：某一关键帧与该关键帧共同观测（共视）到的地图点的关键帧，也称一级关键帧。共同观测到相同特征点的数目称为共视程度。
• 共视图：共视图的节点是关键帧，若两个关键帧的共视地图点超过某一阈值（>=N)，则用边连接，构成无向加权图，边的权重为共视点的数量。

3. 共视图、生成树、本质图的关系

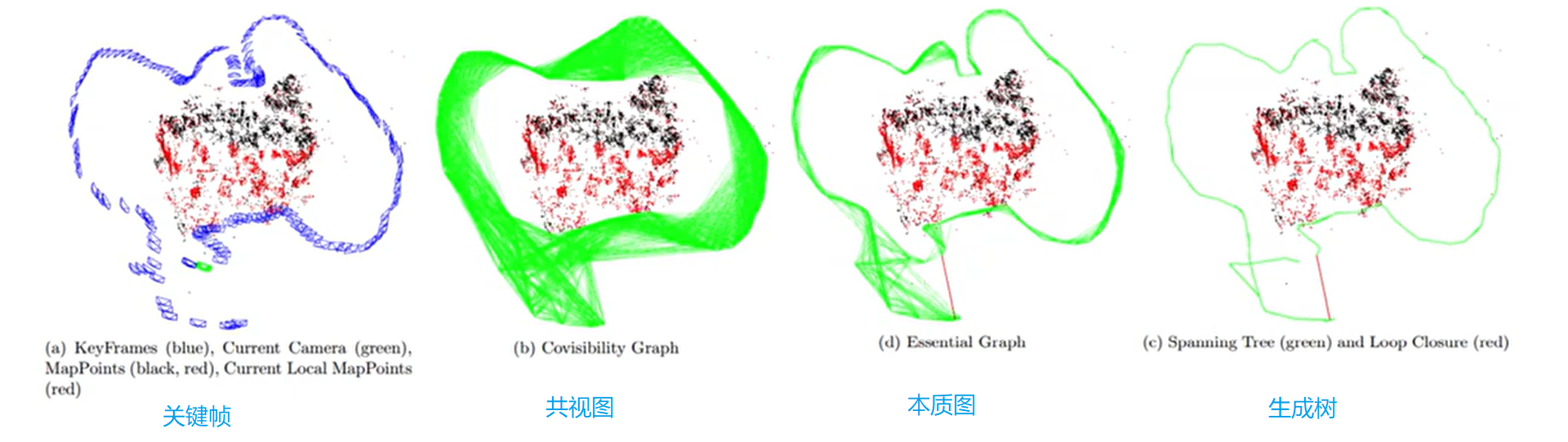
• 共视图 Covisibility Graph：共视图是一个加权无向图，图中每个节点是相机的位姿，如果两个位姿的关键帧拍摄到的相同关键点的数量达到一定值（论文设定为至少15个），则认为两个关键帧具有共视关系。此时两个节点之间便生成了一条边，边的权重与共视点的数量有关。

• 生成树 Spanning Tree：用最少的边连接了所有的关键帧节点（即共视图中所有的节点）。当一个关键帧被加入到共视图当中后，这个关键帧与共视图中具有最多观测点的关键帧之间建立一个边，完成 Spanning Tree 的增长。

• 本质图 Essential Graph：根据共视关系得到的共视图是一个连接关系非常稠密的图，即节点之间有较多的边，而这过于稠密而不利于实时的优化。于是构建了 Essential Graph，在保证连接关系的前提下尽可能减少节点之间的边。Essential Graph 中的节点依旧是全部的关键帧对应的位姿，连接的边包含三种边：Spanning Tree 的边、共视图中共视关系强（共视点数量超过100）的边、以及回环时形成的边。

相同点在于都是以关键帧作为节点，帧与帧之间通过边来连接的模型。不同点在于：

• 共视图(Covisibility Graph)最稠密，本质图(Essential Graph)次之，生成树(Spanning tree)最稀疏。
• 共视图保存了关键帧与所有共视关键点大于某一阈值的的共视帧之间的关系。
• 本质图包含生成树的连接关系、形成闭环的连接关系、共视关系很好的连接关系(共视关键点 $>=100$ )。
• 生成树只包含了关键帧与附近共视关系最好的关键帧。

4、IMU 预积分

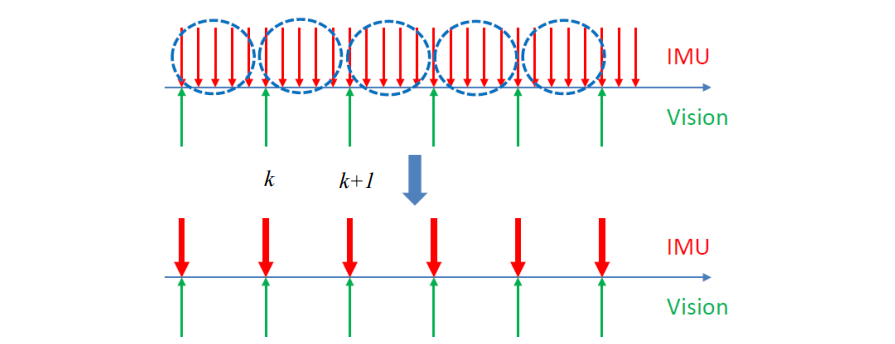
如图，IMU 量测值频率远高于时间量测，假设了短时间内的积分项为常数，将第 $k$ 帧和第 $k+1$ 帧之间的所有 IMU 进行积分，通过迭代优化估计非积分项的状态值，可得第 $\mathrm{k}+1$ 帧的位置、速度和旋转 (PVQ)，作为视觉估计的初始值，避免了优化过程中的重复积分，主要是为了提高计算效率。具体原理如下：

IMU（Inertial measurement unit）惯性测量单元，包括加速度计和角速度。加速度计用于测量物体的加速度，陀螺仪可以测量物体的三轴角速度。IMU 与视觉 SLAM 的互补：

• IMU 可以为视觉 SLAM 提供：尺度信息、重力方向、速度。
• 视觉 SLAM 可以得到 IMU 的 Bias。

IMU 得到的数据包括角速度和加速度、可以通过积分得到速度和位置： $$ \begin{aligned}{ }{\mathrm{B}} \tilde{\boldsymbol{\omega}}{\mathrm{WB}}(t) & ={ }{\mathrm{B}} \boldsymbol{\omega}{\mathrm{WB}}(t)+\mathbf{b}^{g}(t)+\boldsymbol{\eta}^{g}(t) \ { }{\mathrm{B}} \tilde{\mathbf{a}}(t) & =\mathrm{R}{\mathrm{wB}}^{\top}(t)\left({ }{\mathrm{w}} \mathbf{a}(t)-{ }{\mathrm{w}} \mathbf{g}\right)+\mathbf{b}^{a}(t)+\boldsymbol{\eta}^{a}(t),\end{aligned} $$ 由于 IMU 得到的数据时离散的，所以通过累加和的方式得到旋转、速度和平移数据： $$ \begin{array}{l}\mathrm{R}{j}=\mathrm{R}{i} \prod_{k=i}^{j-1} \operatorname{Exp}\left(\left(\tilde{\boldsymbol{\omega}}{k}-\mathbf{b}{k}^{g}-\boldsymbol{\eta}{k}^{g d}\right) \Delta t\right) \ \mathbf{v}{j}=\mathbf{v}{i}+\mathbf{g} \Delta t{i j}+\sum_{k=i}^{j-1} \mathrm{R}{k}\left(\tilde{\mathbf{a}}{k}-\mathbf{b}{k}^{a}-\boldsymbol{\eta}{k}^{a d}\right) \Delta t \ \mathbf{p}{j}=\mathbf{p}{i}+\sum_{k=i}^{j-1}\left[\mathbf{v}{k} \Delta t+\frac{1}{2} \mathbf{g} \Delta t^{2}+\frac{1}{2} \mathrm{R}{k}\left(\tilde{\mathbf{a}}{k}-\mathbf{b}{k}^{a}-\eta_{k j}^{a d}\right) \Delta t_{j}^{2}\right]\end{array} $$ 上式旋转、速度和平移量都是耦合在一起的，计算量太大。可以将这三个量解耦，只需通过 IMU 的读数和前一时刻的预积分量就可以更新当前的预积分量： $$ \begin{aligned} \Delta \mathrm{R}{i j} & \doteq \mathrm{R}{i}^{\top} \mathrm{R}{j}=\prod{k=i}^{j-1} \operatorname{Exp}\left(\left(\tilde{\boldsymbol{\omega}}{k}-\mathbf{b}{k}^{g}-\boldsymbol{\eta}{k}^{g d}\right) \Delta t\right) \ \Delta \mathbf{v}{i j} & \doteq \mathrm{R}{i}^{\top}\left(\mathbf{v}{j}-\mathbf{v}{i}-\mathbf{g} \Delta t{i j}\right)=\sum_{k=i}^{j-1} \Delta \mathrm{R}{i k}\left(\tilde{\mathbf{a}}{k}-\mathbf{b}{k}^{a}-\boldsymbol{\eta}{k}^{a d}\right) \Delta t \ \Delta \mathbf{p}{i j} & \doteq \mathrm{R}{i}^{\top}\left(\mathbf{p}{j}-\mathbf{p}{i}-\mathbf{v}{i} \Delta t{i j}-\frac{1}{2} \sum_{k=i}^{j-1} \mathbf{g} \Delta t^{2}\right) \ & =\sum_{k=i}^{j-1}\left[\Delta \mathbf{v}{i k} \Delta t+\frac{1}{2} \Delta \mathrm{R}{i k}\left(\tilde{\mathbf{a}}{k}-\mathbf{b}{k}^{a}-\boldsymbol{\eta}_{k}^{a d}\right) \Delta t^{2}\right]\end{aligned} $$

5、VIO 视觉惯性里程计

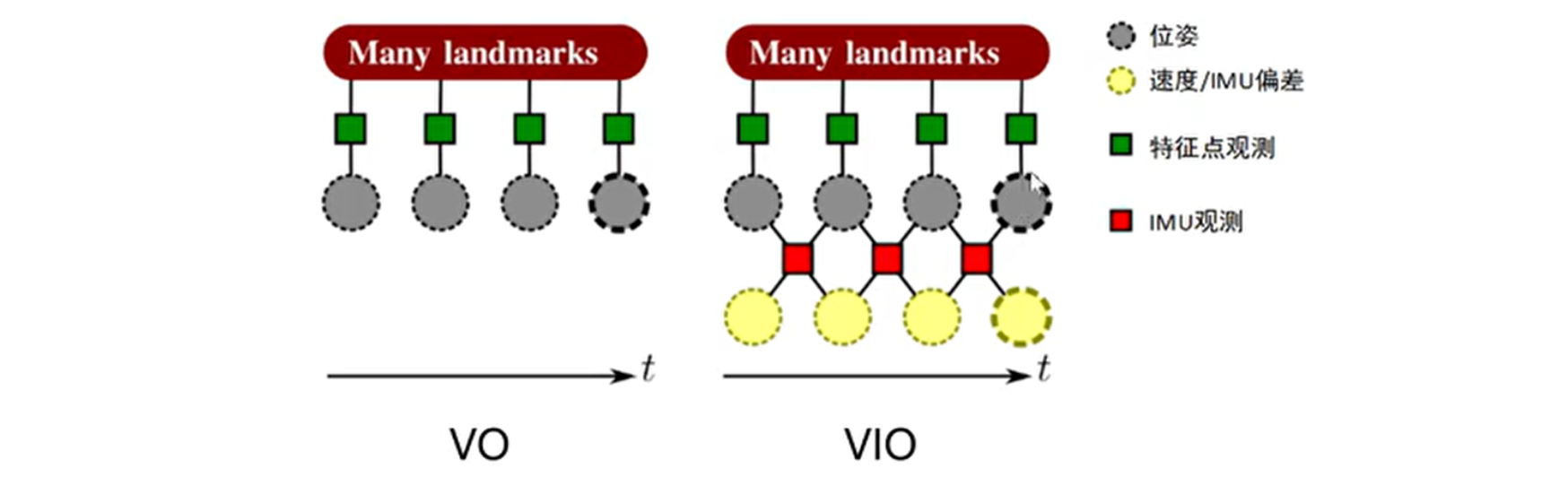
视觉里程计 VO 通过最小化相机帧中地标的重投影误差，计算得到相机的位姿和地标的位置。IMU 对相邻两位姿直接进行约束，而且对没有帧添加了状态量：陀螺仪和加速度计的 Bias 及速度。

对于这样的结构，建立一个包含重投影误差和 IMU 误差项的统一损失函数进行联合优化： $$ J(x)=\underbrace{\sum_{i=1}^{l} \sum_{k=1}^{K} \sum_{j \in J(i, k)} e_{r}^{i, j, k T} W_{r}^{i, j, k} e_{r}^{i, j, k}}{\text {visual }}+\underbrace{\sum{k=1}^{K-1} e_{s}^{k T} W_{s}^{k} e_{s}^{k}}{\text {inertial }} $$ 其中， $i, j, k$ 分别表示相机、特征点和关键帧的索引， $W{r}^{i, j, k}$ 表示特征的信息矩阵， $W_{s}^{k}$ 表示IMU 误差的信息矩阵，而 $e_{r}^{i, j, k}$ 为视觉重投影误差， $e_{s}^{k}$ 为 $\mathrm{IMU}$ 误差项。

6、相机模型

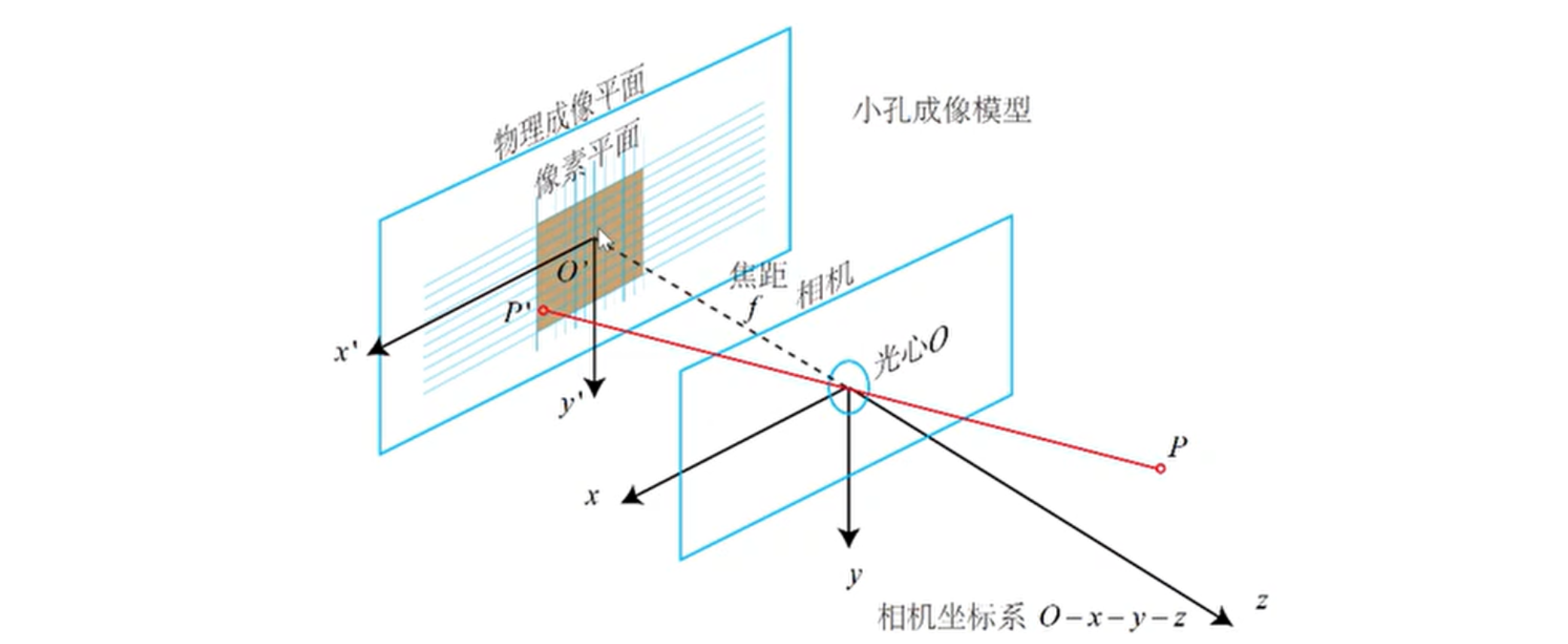
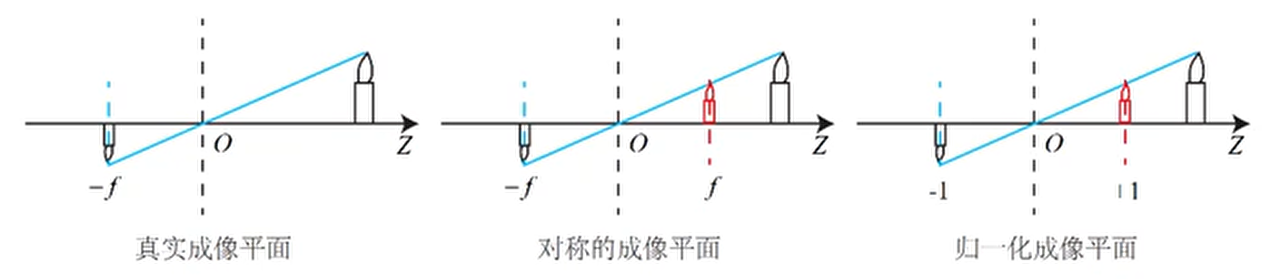
相机将三维世界的坐标点投影到二维平面的过程可以用一个几何模型表示，其中最简单的模型是针孔模型，即物理中的小孔成像原理。

$O-x-y-z$ 为相机坐标系， $O-x^{\prime}-y^{\prime}-z$ 为物理成像平面。空间点 $P$ 通过小孔 $O$ 投影到物理成像平面 ，成像点为 $P^{\prime}$ 。$P$ 的坐标为 $[X, Y, Z], P^{\prime}$ 的坐标为 $\left[X^{\prime}, Y^{\prime}, Z^{\prime}\right]$，物理成像平面到小孔的距离 (即焦距) 为 $f$ 。根据三角形的相似关系，存在： $$ \frac{Z}{f}=-\frac{X}{X^{\prime}}=-\frac{Y}{Y^{\prime}} $$ 其中负号表示成像是倒立的。为简化模型，可以将成像平面对称到相机前面 ，即将空间点 $P$ 一起放在相机坐标的同一侧。

则有： $$ \frac{Z}{f}=\frac{X}{X^{\prime}}=\frac{Y}{Y^{\prime}} \Longrightarrow \begin{aligned} X^{\prime} & =f \frac{X}{Z} \ Y^{\prime} & =f \frac{Y}{Z}\end{aligned} $$ 在相机中获得的像素，需要对物理成像平面上对成像进行采样和量化。因此，假设在物理成像平面上存在一 个像素平面 $O-u-v$ ，设空间点 $P$ 在像素平面的投影为 $P^{\prime}$ ，其坐标为 $[u, v]^{T}$ 。像素坐标系与成像平面之间，相差一个缩放和原点的平移。 $$ P^{\prime} \text { 的坐标 }\left{\begin{array}{l} u=\alpha X^{\prime}+c_{x} \ v=\beta Y^{\prime}+c_{y} \end{array}\right. $$ 其中， $\alpha$ 和 $\beta$ 是缩放系数， $\left[c_{x}, c_{y}\right]$ 是原点的平移。 $$ \begin{array}{ll} X^{\prime}=f \frac{X}{Z} & f_{x}=\alpha f \ Y^{\prime}=f \frac{Y}{Z} & f_{y}=\beta f \end{array} \Rightarrow\left{\begin{array}{l} u=f_{x} \frac{X}{Z}+c_{x} \ v=f_{y} \frac{Y}{Z}+c_{y} \end{array}\right. $$

$$ \left{\begin{array}{l}u=f_{x} \frac{X}{Z}+c_{x} \ v=f_{y} \frac{Y}{Z}+c_{y}\end{array} \stackrel{\text { 矩阵形式 }}{\rightleftarrows}\left(\begin{array}{l}u \ v \ 1\end{array}\right)=\frac{1}{Z}\left(\begin{array}{ccc}f_{x} & 0 & c_{x} \ 0 & f_{y} & c_{y} \ 0 & 0 & 1\end{array}\right)\left(\begin{array}{c}X \ Y \ Z\end{array}\right) \triangleq \frac{1}{Z} \boldsymbol{K} \boldsymbol{P}\right. $$

将 $Z$ 移到左边： $$ Z\left(\begin{array}{l} u \ v \ 1 \end{array}\right)=\left(\begin{array}{ccc} f_{x} & 0 & c_{x} \ 0 & f_{y} & c_{y} \ 0 & 0 & 1 \end{array}\right)\left(\begin{array}{l} X \ Y \ Z \end{array}\right) \triangleq \boldsymbol{K} \Rightarrow \boldsymbol{P}{u v}=Z\left[\begin{array}{l} u \ v \ 1 \end{array}\right]=\boldsymbol{K}\left(\boldsymbol{R} \boldsymbol{P}{w}+\boldsymbol{t}\right)=\boldsymbol{K} \boldsymbol{T} \boldsymbol{P}{w} $$ 中间矩阵称为相机的内参数矩阵 (Camera Intrinsics) $\boldsymbol{K}$ ，相机的位姿 $R, t$ 又称为相机的外参数 (Camera Extrinsics)。相比于不变的内参，外参会随着相机运动发生改变，同时也是 SLAM 中待估计的目标，代表相机 的运动轨迹。 $$ Z \boldsymbol{P}{u v}=Z\left[\begin{array}{c} u \ v \ 1 \end{array}\right]=\boldsymbol{K}\left(\boldsymbol{R} \boldsymbol{P}{w}+\boldsymbol{t}\right)=\boldsymbol{K} \boldsymbol{T} \boldsymbol{P}{w} $$ 上式表明：可以把一个世界坐标点先转换到相机坐标系，再去掉它最后一维的数值 (即该点距离相机成像平面的深度）。相当于归一化处理，得到点 $P$ 在相机归一化平面上的投影： $$ \left(R P_{w}+t\right)=\underbrace{[X, Y, Z]}_{\text {相机坐标 }} \rightarrow \frac{[X / Z, Y / Z, 1]}{[\text { 归一化坐标 }} $$ 归一化坐标可以看成相机前方 $z=1$ 处的平面上的一点， $z=1$ 平面又称为归一化平面。归一化坐标左乘相机内参 $K$ ，就得到像素坐标。因此，也可以把像素坐标 $[u, v]^{T}$ 看成对归一化平面上点进行量化测量的结果。

7、多视图几何

多视图几何是计算机视觉领域一种应用广泛的建模方法，它可以通过多帧图像之间特征的匹配关系建立拍摄这些图像时的相机位姿之间的联系，目的是进行运动估计，根据特征点匹配情况，求解出旋转矩阵 $\mathrm{R}$ 和平移向量 $t$。多视图几何方法从几何的角度构造特征坐标的等量约束关系，而相机位姿信息则蕴含在这些约束关系之中。多视图几何包括对极几何、单应性与三焦张量：

• 对极几何：描述同一个空间点在两个相机视图中的坐标关系，连接此点与一个相机光心所构成的线段将在另一个相机的视图中形成一条线，称作极线。此点在第二个相机视图中所成的像必然位于此极线上：

  

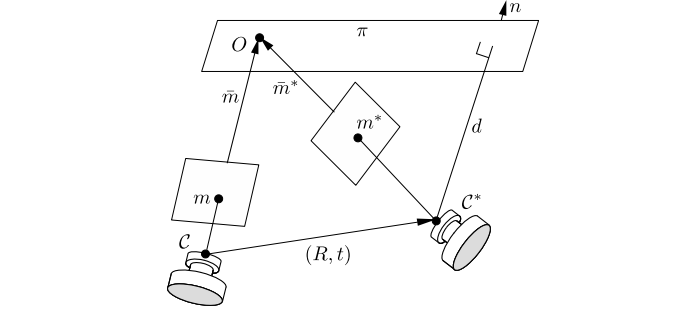
• 单应性：同样描述两个相机视图之间的映射关系，考虑处于空间中一个平面上的特征点，它一个相机中所成的像必然可以通过一个投影变换转化为其在另一个相机图像中的像，而此投影变换正是由其所在的平面来决定：

  

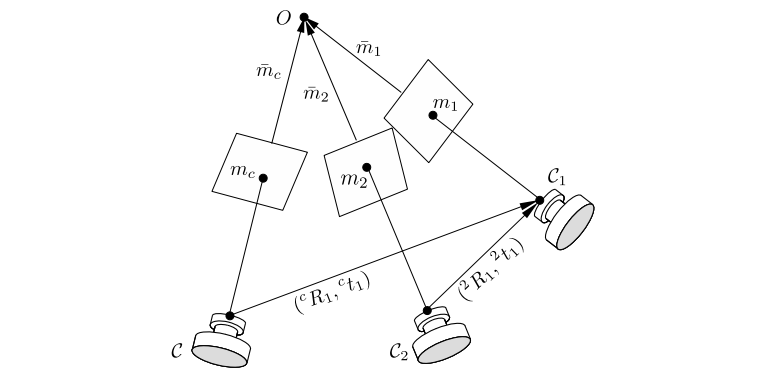
• 三焦张量：描述同一个空间点在三个相机视图中的坐标关系，可以将这三个视图分成两组，分别按照对极几何或单应性进行几何约束关系的构造，最终即可整合成一个整体的约束关系：

  

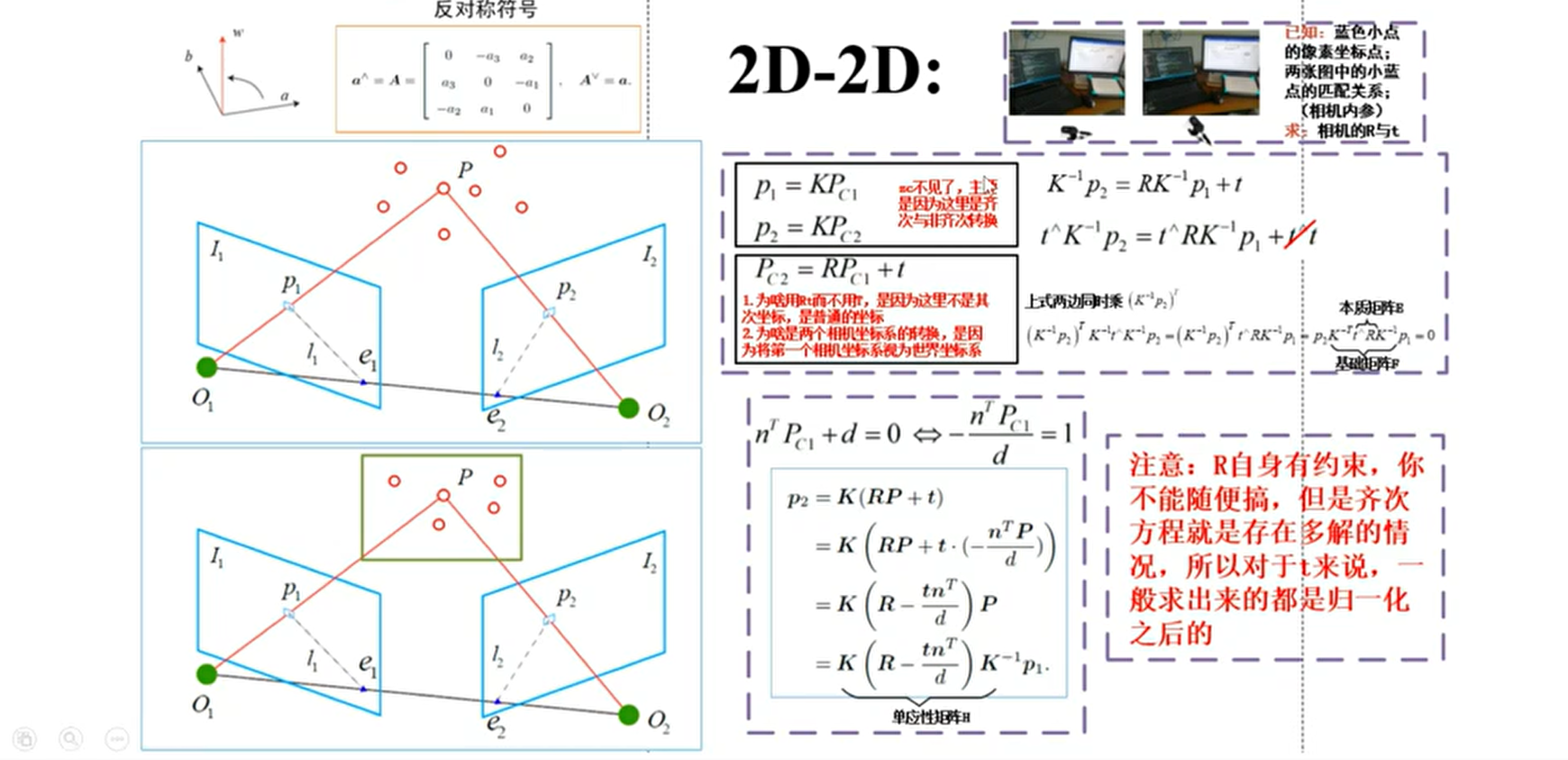
针对特征点匹配的情况，运动估计可以分为：2D-2D、3D-2D、3D-3D。

1. 2D-2D

2D-2D 主要是针对单目相机的初始化过程，在不知道空间中 3D 点的情况下（如末进行初始化）通过两帧间匹配的特征点进行帧间相机运动估计。当相机为单目相机，只知道 2D 的像素坐标，如何根据两组 2D 点估计相机运动，该问题用对极几何解决。

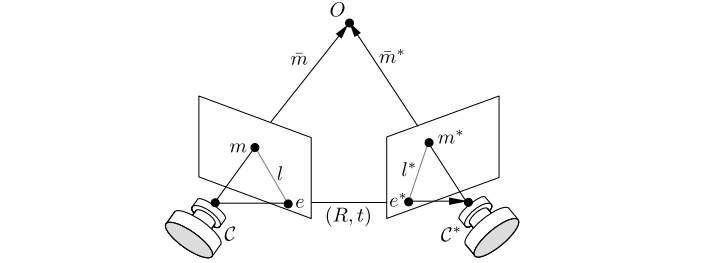
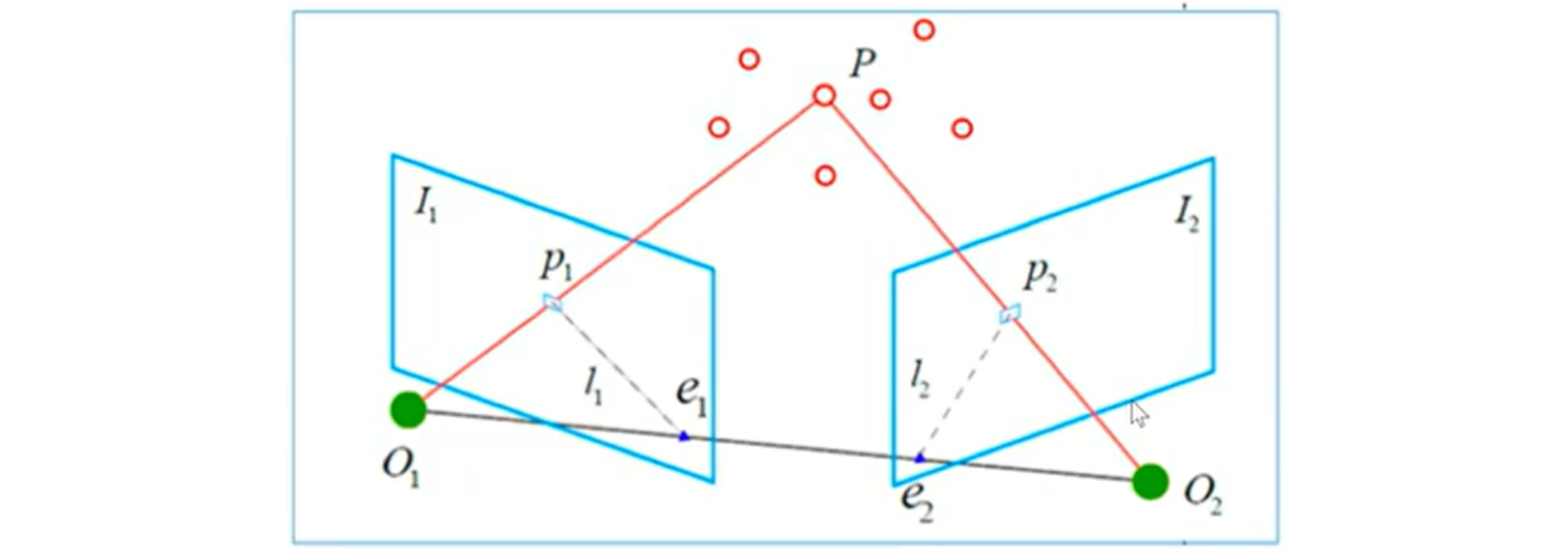
如图， $I_{1}$ 是第一帧， $I_{2}$ 是相机运动后的第二帧， $O_{1}$ 和 $O_{2}$ 是运动前后的相机中心。假设第一帧到到第二帧的运动 (旋转和平移) 为 $[R, t]$ 。

• $I_{1}$ 中有一个特征点 $p_{1}$ ，它在 $I_{2}$ 中对应的是特征点 $p_{2}$ ，这 两个点是同一个空间点 $P$ 在两个成像平面上的投影。

• 连线 $\overrightarrow{O_{1} p_{1}}$ 和连线 $\overrightarrow{O_{1} p_{2}}$ 在三维空间中相交于点 $P$ ，这时 $O_{1}, O_{2} ， P$ 三个点可以确定一个平面 $O_{1} O_{2} P$ ，称为极平面 (Epipolar plane)。

• $O_{1} O_{2}$ 连线和像平面 $I_{1} ， I_{2}$ 的交点分别为 $e_{1}, e_{2} 。 O_{1} O_{2}$ 被称为基线， $e_{1}$ 和 $e_{2}$ 称为极点(Epipoles)。

• 极平面 $O_{1} O_{2} P$ 与两个像平面 $I_{1} ， I_{2}$ 之间的相交线 $l_{1} ， l_{2}$ 为极线 (Epipolar line)。

几何方法：主要是根据对极几何理论得到两帧间的对应关系根据针孔相机模型，在齐次坐标情况下： $$ \boldsymbol{p}{1}=\boldsymbol{K} \boldsymbol{P}, \quad \boldsymbol{p}{2}=\boldsymbol{K}(\boldsymbol{R P}+\boldsymbol{t}) $$ 现在，取： $$ \boldsymbol{x}{1}=\boldsymbol{K}^{-1} \boldsymbol{p}{1}, \quad \boldsymbol{x}{2}=\boldsymbol{K}^{-1} \boldsymbol{p}{2} . $$ 其中， $x_{1}, x_{2}$ 是两个像素点的归一化平面上的坐标。 代入上式子，可得： $$ x_{2}=\boldsymbol{R} x_{1}+\boldsymbol{t} . $$ 两边同时左乘 $t$ 的反对称矩阵 $t^{\wedge}$ ，接着同时左乘 $x_{2}^{T}$ ，可得： $$ \boldsymbol{x}{2}^{T} \boldsymbol{t}^{\wedge} \boldsymbol{x}{2}=\boldsymbol{x}{2}^{T} \boldsymbol{t}^{\wedge} \boldsymbol{R} \boldsymbol{x}{1} $$ $t^{\wedge} x_{2}$ 是一个与 $t$ 和 $x_{2}$ 都垂直得到向量，则 $x_{2}^{T} t^{\wedge} R x_{1}=0$ 可得： $$ \boldsymbol{p}{2}^{T} \boldsymbol{K}^{-T} \boldsymbol{t}^{\wedge} \boldsymbol{R} \boldsymbol{K}^{-1} \boldsymbol{p}{1}=0 $$ 上述两个式子称为对极约束，它的几何意义是 $O_{1}, O_{2}, P$ 三者共面。对极约束中同时包括平移和旋转。将中间部分记作两个矩阵，基础矩阵(Fundamental Matrix) $\boldsymbol{F}$ 和 本质矩阵(Essential Matrix) $\boldsymbol{E}$。进一步简化对极约束： $$ \begin{array}{c} \boldsymbol{E}=\boldsymbol{t}^{\wedge} \boldsymbol{R} \ \boldsymbol{F}=\boldsymbol{K}^{-T} \boldsymbol{E} \boldsymbol{K}^{-1} \ \boldsymbol{x}{2}^{T} \boldsymbol{E} \boldsymbol{x}{1}=\boldsymbol{p}{2}^{T} \boldsymbol{F} \boldsymbol{p}{1}=0 \end{array} $$ 相机位姿估计问题变为如下两步：

1. 根据配对点的像素位置，求出 $E$ 或 $F$
2. 根据 $E$ 或 $F$，求出 $R$ 和 $t$

由于 $E$ 和 $F$ 只差相机内参 $K$，而内参由相机提供，通常已知。所以实际情况中，采用形式更简单的本质矩阵 $E$。本质矩阵是一个 $3 \times 3$ 的矩阵，内有 9 个末知数。由于旋转和平移各有 3 个自由度，故 $t^{\wedge} \boldsymbol{R}$ 共有 6 个自由度，但由于尺度等价性， $E$ 实际上有 5 个自由度。估算 $E$ 通常使用 8 对点，也称为八点法(Eight-Point-Algorithm)。八点法只利用 $E$ 的线性性质，因此可以在线性代数框架下求解。

根据估算得到本质矩阵 $E$ ，恢复出相机的运动 $R$ 和 $t$ 。 这个过程采用奇异值分解，假设 $E$ 的SVD 为： $$ \boldsymbol{E}=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{T} $$ 其中 $U$ 和 $V$ 是正交阵， $\boldsymbol{\Sigma}$ 是奇异值矩阵。可以求得： $$ \begin{array}{l} \boldsymbol{t}{1}^{\hat{1}}=\boldsymbol{U} \boldsymbol{R}{Z}\left(\frac{\pi}{2}\right) \boldsymbol{\Sigma} \boldsymbol{U}^{T}, \quad \boldsymbol{R}{1}=\boldsymbol{U} \boldsymbol{R}{Z}^{T}\left(\frac{\pi}{2}\right) \boldsymbol{V}^{T} \ \boldsymbol{t}{\hat{2}}^{\hat{}}=\boldsymbol{U} \boldsymbol{R}{Z}\left(-\frac{\pi}{2}\right) \boldsymbol{\Sigma} \boldsymbol{U}^{T}, \quad \boldsymbol{R}{2}=\boldsymbol{U} \boldsymbol{R}{Z}^{T}\left(-\frac{\pi}{2}\right) \boldsymbol{V}^{T} \end{array} $$ 从 $E$ 分解到 $R$ 和 $t$，存在 $4$ 个可能的解：

$P$ 在两个相机中都有正的深度是正确的解。实际中 ，将一个点代入 4 种解中，检测该点在两个相机下的深度，即可确定哪个是正确的解。

【总结】2D-2D

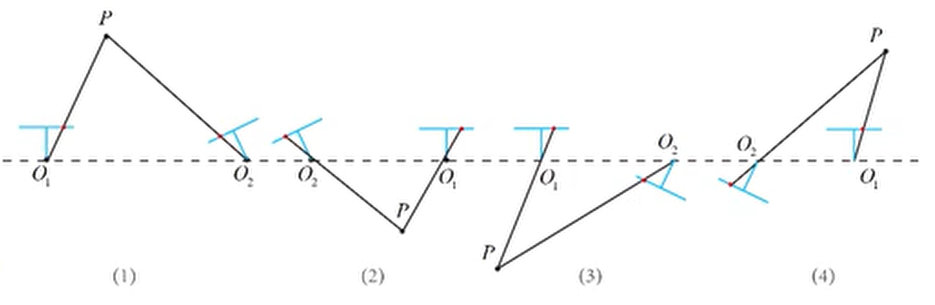
• 八点法求本质矩阵 $E$；
• 本质矩阵奇异值分解得到 4 个解；
• 把一个点带入 4 个解中，看哪个解深度为正值，即为正确的解。

2. 3D-2D

如果一组为 3D，一组为 2D，即知道了一些 3D 点和它们在相机的投影位置，也能估计相机的运动。该问题用 PnP(Perspective-n-Point) 解决。$\mathrm{PnP}$ 是求解 3D 到 2D 点对运动的方法。它描述了当知道 $n$ 个 $3 \mathrm{D}$ 空间点及其投影位置时，如何估计相机的位姿。

• 在双目或 RGB-D 的视觉里程计中，可以直接使用 PnP 估计相机运动;
• 在单目视觉里程计中，必须先进行初始化，才能使用 PnP。

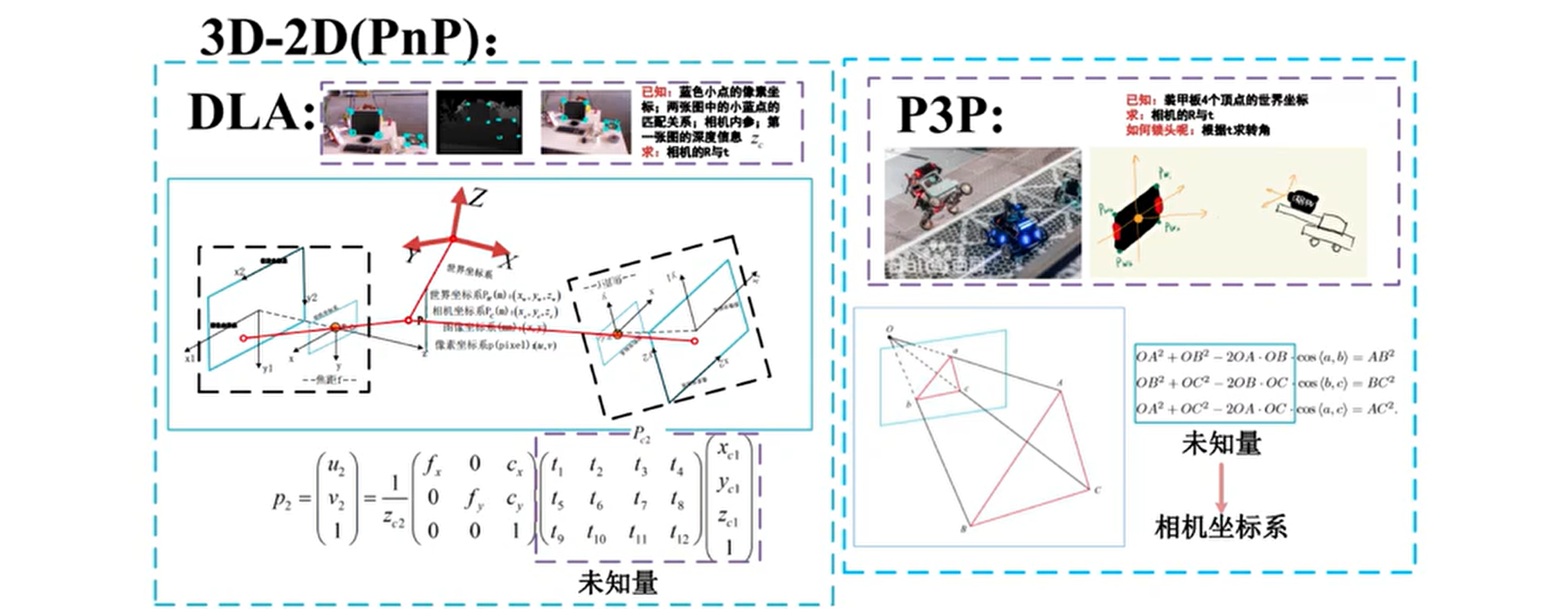
PnP 有如下解法：

• P3P：3 对匹配点，需要相机内参。
• DLT：不需要相机内参，4 点法求单应矩阵，DLT 分解出 K、R、t。
• EPnP：最少4个点，性价比高，精度较高，需要相机内参。
• UPnP：估计出焦距，适合末标定场景。
• BA：构建最小二乘法优化相机位姿。

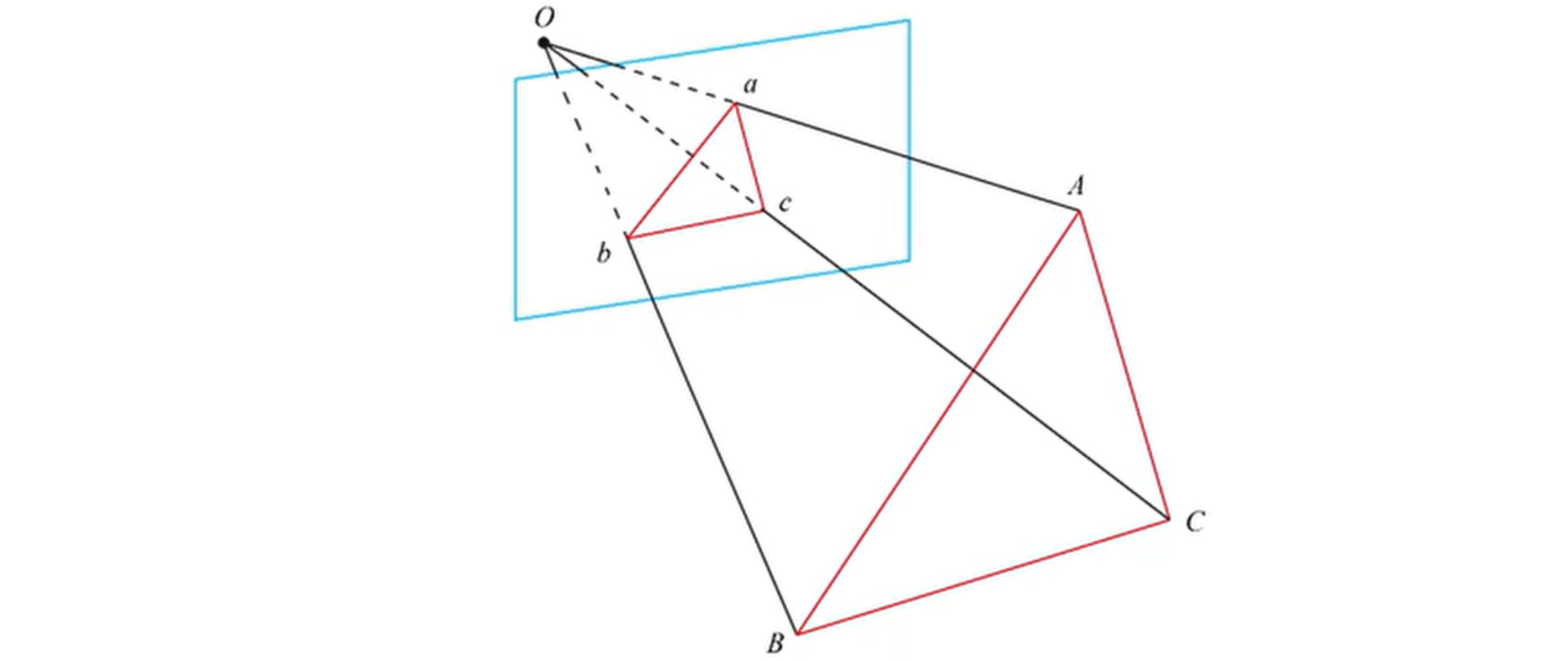
其中 P3P 需要利用给定的 3 个点的几何关系，它的输入数据为 3 对 2D-2D 的匹配点。

其中：3D点 (世界坐标系) : $A, B, C$ 。2D点 (相机坐标系)： $a, b, c$ 分别对应 $A, B, C$ 在相机成像平面上的投影。

$P n P$ 问题转换为 ICP问题:

• 通过余弦定理，可以得到 $O A, O B, O C$ 的长度；
• 3D点在相机坐标下的坐标能够计算出；
• 3D (相机坐标系) - 3D (相机坐标系) 的对应点；
• PnP 问题转换为 ICP问题。

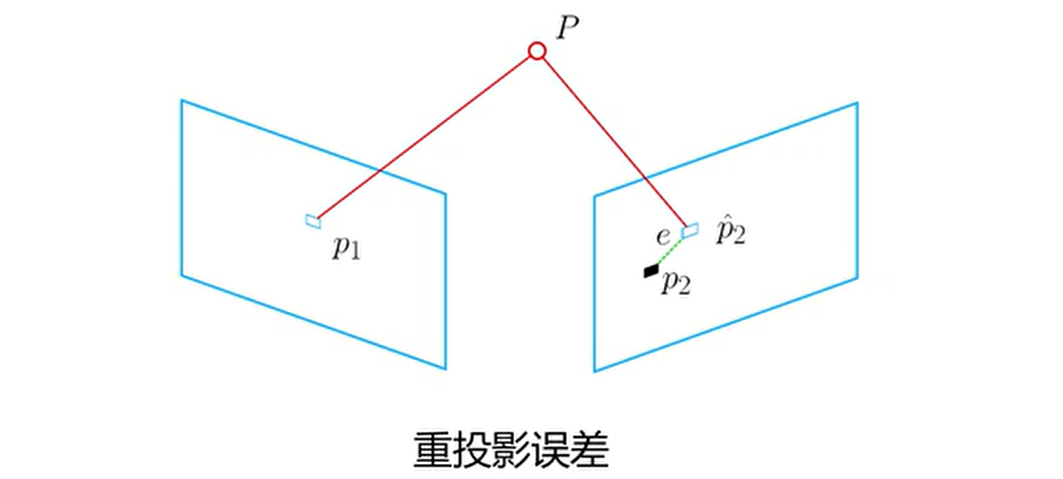
除了线性方法，还可以将 PnP 问题构建为关于重投影误差的非线性最小二乘法问题。线性方法往往先求相机位姿，再求空间点位置，而非线性优化则是把它们都作为优化变量一起优化。 这一类把相机和三维点放在一起进行最小化的问题，称为光束法平差 (Bundle Adjustment，BA)。重投影误差是指将三维点云数据或深度图像中的点投影回二维图像中，再与实际观测到的二维图像中的对应点之间的误差：

考虑到相机位姿末知及观测点的噪声，将误差和构建为最小二乘法问题，使误差最小化，寻找最优的相机位姿： $$ \boldsymbol{\xi}^{*}=\arg \min {\boldsymbol{\xi}} \frac{1}{2} \sum{i=1}^{n}\left|\boldsymbol{u}{i}-\frac{1}{s{i}} \boldsymbol{K} \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{P}{i}\right|{2}^{2} $$ 该问题的误差项是将 $3 D$ 点的投影位置与观测位置作差，因此，称为重投影误差。

3. 3D-3D

3D-2D 当相机为双目、RGB-D 时，或者通过某种方式得到了距离信息，根据两组 3D 点估计相机运动。该问题用 ICP(Iterative Closest Point) 解决。

假设有一组配对好的 3D 点： $$ \boldsymbol{P}=\left{\boldsymbol{p}{1}, \ldots, \boldsymbol{p}{n}\right}, \quad \boldsymbol{P}^{\prime}=\left{\boldsymbol{p}{1}^{\prime}, \ldots, \boldsymbol{p}{n}^{\prime}\right} $$ 现在希望找到一个欧式变换 $R, t$ ，使得： $$ \forall i, \boldsymbol{p}{i}=\boldsymbol{R} \boldsymbol{p}{i}^{\prime}+\boldsymbol{t} $$ 该问题使用迭代最近点 ICP 求解。与 PnP 类似，ICP 的求解也分为两种形式：线性优化 SVD、非线性优化：BA。

先来看 SVD 法，分为三个步骤求解：

1. 计算两组点的质心位置 $\boldsymbol{p}, \boldsymbol{p}^{\prime}$, 然后计算每:个点的去质心坐标：

$$ \boldsymbol{q}{i}=\boldsymbol{p}{i}-\boldsymbol{p}, \quad \boldsymbol{q}{i}^{\prime}=\boldsymbol{p}{i} ({\prime}-\boldsymbol{p}){\prime} $$

2. 根据以下优化问题计算旋转矩阵：

$$ \boldsymbol{R}^{*}=\arg \min {\boldsymbol{R}} \frac{1}{2} \sum{i=1}^{n}\left|\boldsymbol{q}{i}-\boldsymbol{R} \boldsymbol{q}{i} ({\prime}\right|){2} $$

3. 根据第二步的 $\boldsymbol{R}$, 计算 $\boldsymbol{t}$：

$$ t^{*}=p-R p^{\prime} $$

展开关于 $R$ 的误差项： $$ \frac{1}{2} \sum_{i=1}^{n}\left|\boldsymbol{q}{i}-\boldsymbol{R} \boldsymbol{q}{i}^{\prime}\right|^{2}=\frac{1}{2} \sum_{i=1}^{n} \boldsymbol{q}{i}^{T} \boldsymbol{q}{i}+\boldsymbol{q}{i}^{\prime T} \boldsymbol{R}^{T} \boldsymbol{R} \boldsymbol{q}{i}^{\prime}-2 \boldsymbol{q}{i}^{T} \boldsymbol{R} \boldsymbol{q}{i}^{\prime} $$ 第一项与 $R$ 无关，第二项 $R^{T} R=I$ ，也与 $R$ 无关。 则实际的优化目标函数为： $$ \sum_{i=1}^{n}-\boldsymbol{q}{i}^{T} \boldsymbol{R} \boldsymbol{q}{i}^{\prime}=\sum_{i=1}^{n}-\operatorname{tr}\left(\boldsymbol{R} \boldsymbol{q}{i}^{\prime} \boldsymbol{q}{i}^{T}\right)=-\operatorname{tr}\left(R \sum_{i=1}^{n} \boldsymbol{q}{i}^{\prime} \boldsymbol{q}{i}^{T}\right) $$ 除此之外，求解 ICP 的非线性方法，用迭代的方式寻找最优值。利用李代数优化相机位姿时，目标函数为: $$ \min {\boldsymbol{\xi}}=\frac{1}{2} \sum{i=1}^{n}\left|\left(\boldsymbol{p}{i}-\exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}{i} ({\prime}\right)\right|{2}){2} $$ 使用李代数扰动模型，可得： $$ \frac{\partial \boldsymbol{e}}{\partial \delta \boldsymbol{\xi}}=-\left(\exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}{i}{ } ({\prime}\right)){\odot} $$ 通过不断迭代，最小化误差，就能找到极小值。一个像素的深度可能有，也可能测量不到，实际情况中常常混合着使用 PnP 和 ICP 优化。

• 深度已知的特征点，建模 3D-3D 误差；
• 深度末知的特征点，建模 3D-2D 的重投影误差。

8、DBoW 词袋模型

BoW（Bag of Words，词袋模型），是自然语言处理领域经常使用的一个概念。以文本为例，一篇文章可能有一万个词，其中可能只有 500 个不同的单词，每个词出现的次数各不相同。词袋就像一个个袋子，每个袋子里装着同样的词。这构成了一种文本的表示方式。这种表示方式不考虑文法以及词的顺序。

在计算机视觉领域，图像通常以特征点及其特征描述来表达。如果把特征描述看做单词，那么就能构建出相应的词袋模型。这就是本文介绍的 DBoW2 库所做的工作。利用 DBoW2 库，图像可以方便地转化为一个低维的向量表示。比较两个图像的相似度也就转化为比较两个向量的相似度。它本质上是一个信息压缩的过程。

词袋模型利用视觉词典（vocabulary）来把图像转化为向量。视觉词典有多种组织方式，对应于不同的搜索复杂度。DBoW2 库采用树状结构存储词袋，搜索复杂度一般在 log(N)，有点像决策树。通过在大量图像中提取特征，利用 K-Means 方法聚类出 $n$ 个单词。这个 $n$ 个单词也不是一次聚类而成的，而是利用了 K 叉树。在每一层依次用 K-means 算法聚类成 $K$ 类。最后形成的叶子节点就是单词。深度为 $d$ 的 $K$ 叉树形成的单词数量为 $n=K^{d}$ 。在 DBoW2 中默认的 $K=10, d=5$ ，可以形成10000个单词。

利用 $K$ 叉树的好处是什么呢? 主要是加速：

1. 可以加速判断一个特征属于哪个单词。如果不使用 K 叉树，就需要与每个单词比较 (计算汉明距离），共计需要比较 $K^{d}$ 次。而使用 K 叉树之后，需要的比较次数变为 $K \times(d-1)$ 次。大大提高了速度。这里利用了 K 叉树的快速查找特性。
2. DBoW 中存储了 Direct Index，也就每个节点存储有一幅图像上所有归属与该节点的特征的 index。在两帧进行特征匹配的时候，只需要针对每一个节点进行匹配就好了，大大缩小了匹配空间，加速了匹配速度。ORB-SLAM帧间匹配都使用了这个trick。
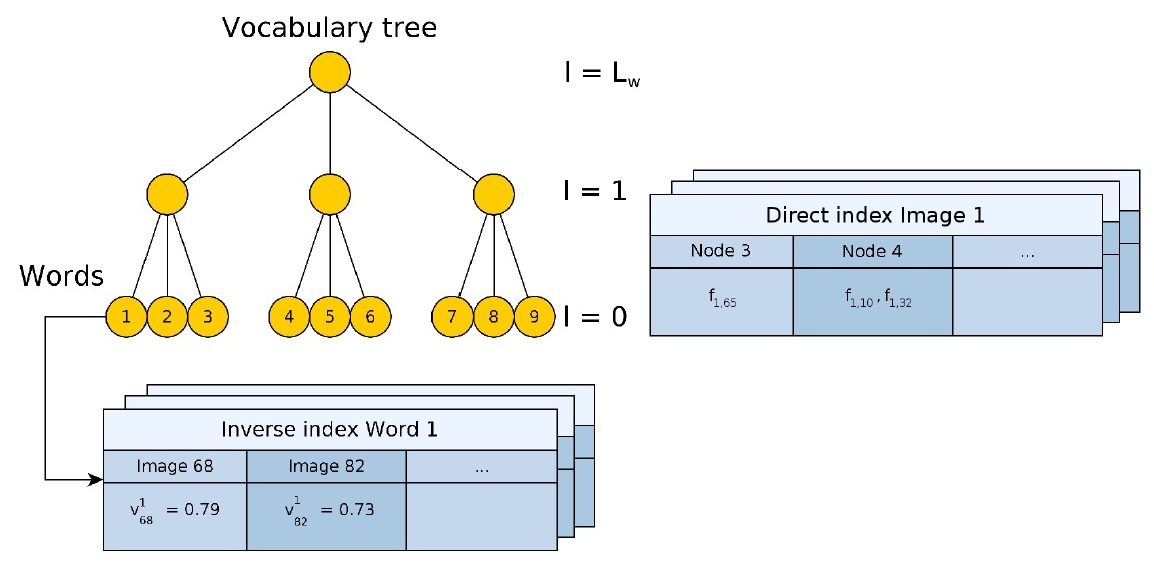
3. 除此之外，如下图，DBoW 的每个单词中还存储了 Inverse index，每个 Inverse Index 中存储有所有有此单词的图像 index，以及对应的权重: $<I_{i}, \eta_{i}>$ 。在进行闭环搜索的时候，可以加快搜索过程的。具体的，我们只需要找与当前关键帧有相同单词的关键帧就可以了。
4. 反向索引：记录每个叶节点对应的图像编号。当识别图像时，根据反向索引选出有着公共叶节点的备选图像并计算得分，而不需要计算与所有图像的得分。

• 正向索引：当两幅图像进行特征匹配时，如果极线约束未知，那么只有暴力匹配，正向索引在此时用于加速特征匹配。需要指定词典树中的层数，比如第 m 层。每幅图像对应一个正向索引，储存该图像生成 BoW 向量时曾经到达过的第 m 层上节点的编号，以及路过这个节点的那些特征的编号。假设两幅图像为A和B，下图说明如何利用正向索引来加速特征匹配的计算：

这棵树里面总共有 $1+K+\cdots+K^{L}=\left(k^{L+1}-1\right) /(K-1)$ 个节点。所有叶节点在 $L$ 层形成 $W=K^{L}$ 类，每一类用该类中所有特征的平均特征（meanValue）作为代表，称为单词（word）。每个叶节点被赋予一个权重。作者提供了 TF、IDF、BINARY、TF-IDF 等权重作为备选，默认为 TF-IDF：

• TF 代表词频 (Term Frequency)，表示词条在文档中出现的频率。

• IDF 代表逆向文件频率 (Inverse Document Frequency)。如果包含词条的文档越少，IDF 越大，表明词条具有很好的类别区分能力。

单词的 IDF 越高，说明单词本身具有高区分度。二者结合起来，即可得到这幅图像的 BoW 描述。如果某个词或短语在一篇文章中出现的频率 TF 高，并且在其他文章中很少出现，则认为此词或者短语具有很好的类别区分能力，适合用来分类。最后当前图像的一次单词的权重取为IDF和TF的乘积： $$ \eta_{i}=T F_{i} \times I D F_{i} $$ 这样，就组成了一个带权的词袋向量： $$ A=\left{\left(w_{1}, \eta_{1}\right),\left(w_{2}, \eta_{2}\right), \cdots,\left(w_{N}, \eta_{N}\right)\right}: v_{A} $$ 下面计算两幅图像A，B的相似度，这里就要考虑权重了。计算相似度的方法由很多，DBoW2的库里 面就有L1、L2、ChiSquare等六种计算方式。比如L1距离为： $$ s\left(v_{A}, v_{B}\right)=\frac{1}{2} \sum_{i}\left{\left|v_{A i}\right|+\left|v_{B i}\right|-\left|v_{A i}-v_{B i}\right|\right} $$ 实际上，在比较相似度的时候只需要计算上述的分数就好了，这个速度就比特征匹配快的多。

视觉词典可以通过离线训练大量数据得到。训练中只计算和保存单词的 IDF 值，即单词在众多图像中的区分度。TF 则是从实际图像中计算得到各个单词的频率。单词的 TF 越高，说明单词在这幅图像中出现的越多；离线生成视觉词典以后，我们就能在线进行图像识别或者场景识别。

9、Atlas 地图集

Atlas翻译为“地图集”，即管理着一系列的子地图（sub-map），这些子地图共用同一个 DBoW 数据库，使得能够实现重定位回环等操作。

当相机在正常跟踪状态，所生成关键帧所在的地图称为活动地图（active map）。如果跟踪失败，首先将进行重定位操作寻找地图集中对应的关键帧，如果依旧失败，则重新创建一个新的地图。此时旧的地图变成了非活动地图（non-active map），新的地图作为活动地图继续进行跟踪与建图过程。在跟踪过程中，当前相机必然是位于活动地图当中，可能存在零或多个子地图。

每次插入关键帧时，都与完整地图的DboW数据库进行匹配。如果发现了相同的场景，且两个关键帧同时位于活动地图，则意味着发生了回环，便按照回环的方式进行融合处理；如果匹配上的关键帧位于非活动地图，则需要将两个子地图进行拼接。ORB-SLAM3 中地图融合的区域被称为焊接窗口（welding window）。

地图无缝融合时，当前活跃的地图吞并对应的非活跃地图。通过一系列步骤将非活跃地图的信息补充到当前活跃地图。具体步骤如下：

**1. 检测：**首先由重识别模块检测出当前关键帧Ka与匹配上的待吞并关键帧Ks，并获取两个子地图当中与匹配上的两个关键帧具有共视关系的关键点和关键帧。

2. 位姿计算：通过 Horn+RANSAC 方法初步计算两个关键帧之间的变换关系，之后将待吞并地图的地图点通过这个变换投射到当前关键帧Ka上，再利用引导匹配的方法获得更丰富的匹配并进行非线性优化，获得精确的变换。

**3. 地图点合并：**将被吞并地图的关键点变换到当前关键帧位姿下，融合重复的地图点。之后将两个地图的关键帧融合，重新生成生成树和共视图。

**4. 衔接区域的局部 BA 优化：**融合后与Ka具有共视关系的关键帧参与局部BA优化，为避免 gauge freedom，固定之前活跃地图中的关键帧而移动其他的关键帧。优化完成后再次进行地图点的合并与生成树、共视图的更新。

**5. 完整地图的位姿图优化：**对整个合并后的地图进行位姿图优化。

10、因子图优化状态估计模型

状态估计问题，就是是寻找 $X$ 来最好地描述观测值 $Z$。根据贝叶斯法则，状态量 $X$ 和观测量 $Z$ 的联合概率等于条件概率乘以边缘概率： $$ {P(X,Z) =P(Z \mid X) P(X)} $$ 式中：$P(Z|X)$ 为观测量 $Z$ 对应的概率；$P(X)$ 是状态量 $X$ 的先验概率。后验分布 $P(X|Z)$ 是一种常用且直观评估状态集和 观测集之间拟合程度的方法，我们求解期望的状态集可以由通过后验分布的最大化来实现，也就是极大验后估计： $$ \hat{X}=\underset{X}{\arg \max } P(X \mid Z) $$

有些文章用极大似然估计来介绍因子图优化，都可以，极大后验估计是极大似然估计在包含了先验“量测”后的特例，就多源融合导航而言，这两种最优估计没有本质上的区别。

用极大似然估计来理解：就视觉/惯性/GNSS 融合导航而言，不同传感器之间的量测，以及同一传感器在不同时刻的量测都是独立的，因此全局似然函数可以因式分解成关于各独立量测的似然函数的乘积。

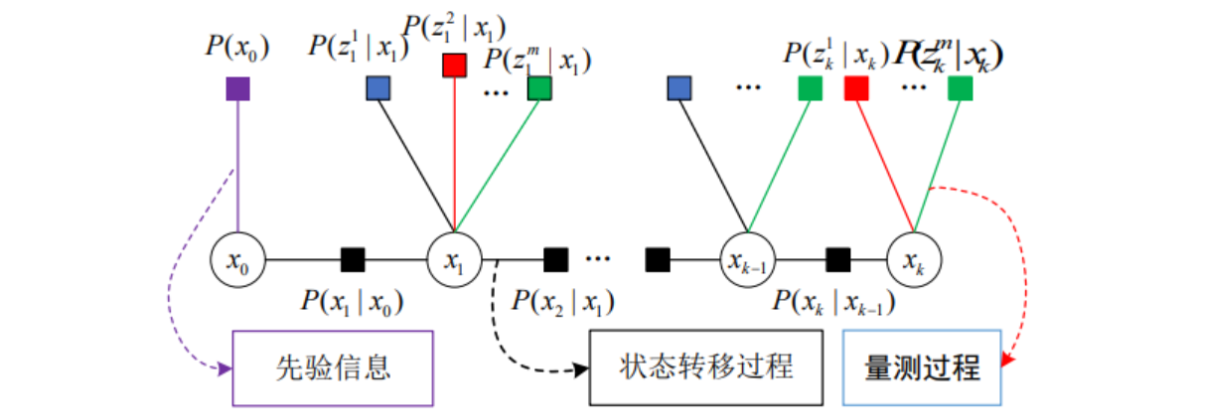
基于因子图的状态估计方法正是将状态估计理解为对系统联合概率密度函数的极大验后估计问题。 一个系统可以描述为状态方程和量测方程两部分，并将状态误差和量测误差视为零均值白噪声即： $$ \left{\begin{array}{rr} x_{k}=f_{k}\left(x_{k-1}, u_{k}\right)+w_{k}, & w_{k} \sim N\left(0, \Sigma_{k}\right) \ z_{k}=h_{k}\left(x_{k}\right)+v_{k}, & v_{k} \sim N\left(0, \Lambda_{k}\right) \end{array}\right. $$ 根据正态分布的特性可以得到真实状态 $k_x$ 和理想量测 $k_z$ 的条件概率分布满足： $$ \left{\begin{array}{l} P\left(x_{k} \mid x_{k-1}\right) \propto e^{-\frac{1}{2}\left|f_{k}\left(x_{k-1}\right)-x_{k}\right|{\varepsilon{k}}^{2}} \ P\left(z_{k} \mid x_{k}\right) \propto e^{-\frac{1}{2} \mid f_{k}\left(x_{k}\right)-z_{k} |{k}^{2}} \end{array}\right. $$ 实际中的状态量 $X$ 往往是不知道的，而当前状态下的观测 $Z$ 是知道的，也就是 $P(Z|X)$ 是知道的，因此在因子图模型中： $$ X{k}^{}=\arg \max P\left(X_{k} \mid Z_{k}\right) \propto \arg \max P\left(X_{k}\right) P\left(Z_{k} \mid X_{k}\right) $$ 其中，$X_{k}=\left{x_{0: k}\right}$ 是状态的集合，$Z_{k}=\left{z_{0:k}^j\right}$ 是所有状态下量测的集合。若系统服从马尔科夫假设，那么： $$ \begin{aligned} X_{k}^{} & =\underset{X_{k}}{\arg \max } P\left(X_{k} \mid Z_{k}\right) \propto \underset{k}{\arg \max } P\left(x_{0}\right) \prod^{k}\left[P\left(x_{i} \mid x_{i-1}\right) \prod_{m_{i}}^{m_{i}}\left[P\left(z_{i}^{j} \mid x_{i}\right)\right]\right] \end{aligned} $$ 对式取对数得到后，将式代入式可以得到，系统的状态估计可等价为全局损失函数的联合优化： $$ X^{*}=\underset{X}{\arg\min } \sum_{i}^{k}\left{\left|f_{i}\left(x_{i-1}, u_{i}\right)-x_{i}\right|{\Sigma{i}}^{2}+\sum_{j=1}^{m_{j}}\left|h_{i}^{j}\left(x_{i}\right)-z_{i}^{j}\right|{\Lambda{i j}}^{2}\right} $$ 上式即为基于因子图优化的估计的一般表达式，其左项为系统状态转移过程，右项为量测过程，$\Sigma$ 和 $\Lambda$ 分别是状态转移过程和量测过程的协方矩阵，进行求解的是状态集合 X 。对于式，可以用下图进行表示：

• 圆圈：变量节点，表示系统待估计的状态，对应一个变量 $x$ 。
• 正方形：因子节点，表示先验信息、状态转移和量测过程，对应一个局部函数 $f$ ，其中：
  • 紫色 $P(x_0)$ 为先验因子。
  • 黑色 $P(x_1|x_0) \dots P(x_k|x_{k-1})$ 为状态转移，由上一时刻状态推测下一时刻状态。
  • 其它为量测信息，$P(z|x)$ 表示在参数 $x$ 的条件下得到观测值 $z$。
• 线：当且仅当变量 $x$ 是局部函数 $f$ 的的自变量时，相应的变量节点和因子节点之间有一条边连接两个节点。
• 若在模型中加入其他传感器，只需将其添加到框架中相关的因子节点处即可。

利用因子图模型对估计系统的联合概率密度函数进行表示，可以直观地反映动态系统的动态演化过程和每个状态对应的量测过程。同时，图形化的表示使系统具有更好的通用性和扩展性。

每一个观测变量在上面贝叶斯网络里都是单独求解的（相互独立），所有的条件概率都是乘积的形式，且可分解，在因子图里面，分解的每一个项就是一个因子，乘积乘在一起用图的形式来描述就是因子图。 整个因子图实际上就是每个因子单独的乘积。 求解因子图就是将这些因子乘起来，求一个最大值，得到的系统状态就是概率上最可能的系统状态。

先找到残差函数 $e(x)$，由因子节点可以得到我们估计的值和实际的测量值之间的差值，即每个因子 $f$ 会对应一个残差函数。根据中心极限定理，绝大多数传感器的噪声是符合高斯分布的，所以每个因子都是用高斯分布的指数函数来定义的。 $$ g(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) $$ 指数函数对应了残差函数，包括两个部分：系统状态量和观测量。 残差函数实际上表示的是用状态量去推测的观测量与实际观测量的区别。 残差函数的表达式一般都是非线性的，可以通过改变变量 $X$ 来使残差函数最小化，残差函数最小，估计的值越符合观测值，套到因子图里面来看，因子图的求解是要所有因子的乘积最大化， $$ \hat{X}=\underset{X}{\arg \max } \prod_{i} \exp \left(-\frac{1}{2}\left|e_{i}(X i)\right|{\Sigma i}^{2}\right) $$ 对于负指数函数形式，每一个因子乘积最大化代表里面的 $e(x)$ 最小化，对目标函数取对数，概论问题转为非线性最小二乘问题： $$ \hat{X}=\underset{X}{\operatorname{arg} \operatorname{max}} \sum{i}\left(e_{\dot{\epsilon}}\left(x_{i}\right)\right)^{2} $$ 非线性最小二乘可以选择高斯-牛顿法、列文博格-马夸尔特或者Dogleg等迭代优化算法求解，高斯-牛顿法比较简单，但稳定性较差，算法可能不收敛；列文博格-马夸尔特引入置信区间概念，约束下降的步长，提高稳定性，Dogleg也类似。**问题性质较好时可用高斯-牛顿法，问题条件恶劣时选择列文博格-马夸尔特或者Dogleg。**几种非线性最小二乘解法比较如下：

• 最速梯度下降法：目标函数在 $x_k$ 处泰勒展开，保留一阶项，$x*= - J(x_k)$，最速下降法过于贪心，容易走出锯齿路线，反而增加迭代次数。
• 牛顿法：二阶泰勒展开，利用二次函数近似原函数。$H*X= - J$，牛顿法需要计算目标函数的海森矩阵阵，计算量大。规模较大时比较困难。
• 高斯-牛顿法（GN）：$f(x)$ 进行一阶泰勒展开，$f(x)$ 而不是 $F(x)$ ，高斯牛顿法用雅各比矩阵 $JJ^T$ 来作为牛顿法中二阶海森阵的近似，$HX=g$，在使用高斯牛顿法时，可能出现 $JJ^T$ 为奇异矩阵或者病态的情况，此时增量稳定性较差，导致算法不收敛。
• 列文伯格–马夸尔特方法（LM）：基于信赖区域理论，是由于高斯-牛顿方法在计算时需要保证矩阵的正定性，于是引入了一个约束，从而保证计算方法更具普适性。$(H+\lambda I)x=g$，当入较小时，$H$ 占主导，近似于高斯牛顿法，较大时，$\lambda * I$ 占主导，接近最速下降法。