An algorithm is a set well-defined instructions to solve a particular problem. Well defined inputs & outputs. Each step should be clear & unambiguous. The same algorithm with the same programming language can be implemented in different ways.
- As a developer, you're going to come across problem that you need to solve. Learning algorithms translates to learning different techniques to efficiently solve those problems. One problem can be solved in many ways using different algorithms.
We evaluate the performance of an algorithm in terms of its input size.
-
Time Complexity: Amount of time taken by an algorithm to run, as a function of input size
-
Space Complexity: Amount of memory taken by an algorithm to run, as a function of input size
By evaluating against the input size, the analysis is not only machine independent but the comparison is also more appropriate.
- There is no one solution that works every single time. It is always good to know multiple ways to solve the problem & use the best solution, given your constraints.
- If your app needs to be very quick & has plenty of memory to work with, you don't have to worry about space complexity.
- If you have very little memory to work with, you should pick a solution that is relatively slower but need less space.
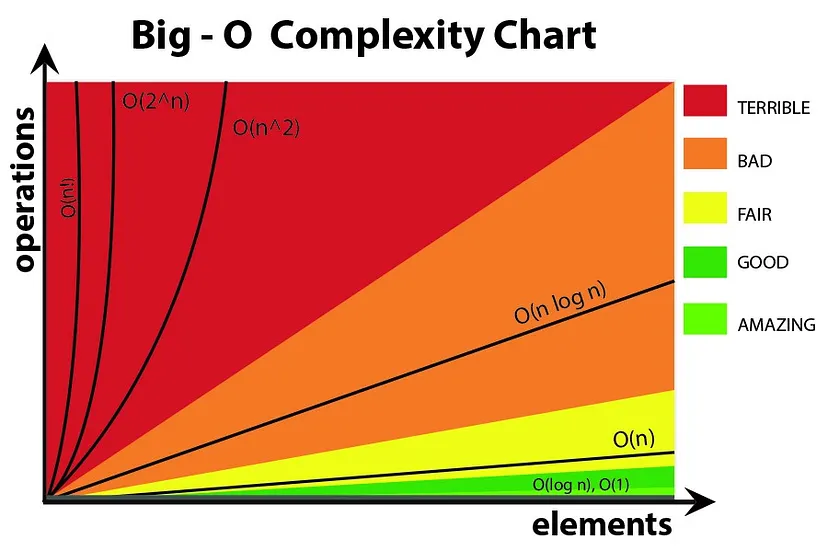
Asymptotic notations : Mathematical tools to represent time & space complexity
- Big-O Notation: Worst case complexity (✅)
- Omega Notation: Best case complexity (❌)
- Theta Notation: Average case complexity (❌)
- Calculation not dependent on Input Size: O(1) - Constant
- One Loop: O(n) - Linear
- Two Nested Loops: O(n^2)
- Input Size reduced by Half: O(log n)
-
Math Algorithms
- Fibonacci Sequence
- Factorial of a Number
- Prime Number
- Power of Two
-
Recursive
- Fibonacci Sequence
- Factorial of a Number
-
Searching Algorithms
- Liner Search
- Binary Search
-
Sorting Algorithms
- Bubble Sort
- Selection Sort
- Insertion Sort
- Merge Sort
- Quick Sort
-
Miscellaneous Algorithms & Problem Solving
- Stack
- Queue
- Single Linked List
- Double Linked List
- Binary Search Tree
- Tree Traversal
- Binary Heaps
- Hash Tables
- Graph
- Graph Traversal