A pure JavaScript (source in TypeScript) Medial (and Scale) Axis Transform (MAT/SAT) library.
Bug reports, pull requests and ⭐⭐⭐⭐⭐s are welcome and appreciated!
Full simple 140 Lines of Code live StackBlitz project
Documentation, but also see installation instructions below.
The MAT is an analytical form of skeletonization of a shape. It is perfectly suited to SVG. Described by many scholars as the most important image transform, it has endless use cases, e.g.:
- Morphing
- Shape thinning and fattening ⭐⭐ NEW ⭐⭐ StackBlitz demo
- Shape classification
- Shape simplification
- Image compression
- Shape Triangulation
The SAT is similar to the MAT (and indeed uses it as input) but is often more practical as it removes insignifacant MAT branches based on the local image scale. The culling severity of branches is controlled by a parameter called s.
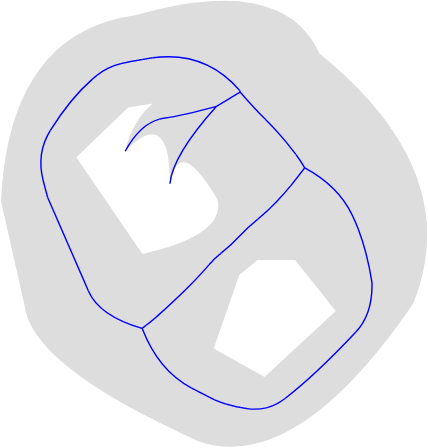
In the image below, the gray silhouette is the original SVG shape and the blue curves represents the SAT. The SAT (and MAT) is internally represented as a tree data structure with branches being quadratic beziers.
FloMat is a MAT/SAT library for planar shapes composed of a closed sequence of linear, quadratic and cubic bezier curves (such as in SVG). The shape need not be simple, can contain holes and may include multiple 'loops'.
For those who are interested, the implementation of the MAT is based on a paper by Hyeong In Choi, Sung Woo Choi, Hwan Pyo Moon and Nam-Sook Wee that can be freely downloaded here. It also gives some valuable insight into the nature of the MAT.
For a less mathematical explanation of the algorithm see this Stack Overflow answer.
The implementation of the SAT is similar to the original ideas that can be found in this paper but it has been improved to preserve topology at any scale >= 1. It also guarantees that the SAT is a subset of the MAT.
Note that the example code given here is in TypeScript since the types make the code clearer but plain JavaScript can also be used.
The live, interactive code can be viewed in this StackBlitz project.
The code can also be found under 'draw-mat-ts' in the examples on GitHub. Only the .css and .ts files are reproduced here.
style.css
h1, h2 {
font-family: Lato;
}
.shape-path {
fill: lightgray;
stroke: darkgray;
stroke-width: 0.1%;
}
.mat {
fill: none;
stroke: deeppink;
stroke-width: 0.1%;
}
.sat {
fill: none;
stroke: blue;
stroke-width: 0.2%;
}index.ts
import './style.css'; // Import stylesheets
import { findMats, getPathsFromStr, Mat, traverseEdges, toScaleAxis } from 'flo-mat';
const NS = 'http://www.w3.org/2000/svg'; // Svg namespace
/**
* Creates and returns an SVG DOM element.
* @param id The dom id to assign to the SVG element, e.g. 1 -> 'svg-1'
*/
function createSvg(id: number) {
let $e = document.createElementNS(NS, 'svg');
$e.setAttributeNS(null, 'id', 'svg' + id);
$e.setAttributeNS(null, 'style', 'width: 100%; display: inline-block');
$e.setAttributeNS(null, 'viewBox', '75 4 557 502');
return $e;
}
/**
* Returns an SVG path string of a line.
* @param ps The line endpoints.
*/
function getLinePathStr(ps: number[][]) {
let [[x0,y0],[x1,y1]] = ps;
return `M${x0} ${y0} L${x1} ${y1}`;
}
/**
* Returns an SVG path string of a quadratic bezier curve.
* @param ps The quadratic bezier control points.
*/
function getQuadBezierPathStr(ps: number[][]) {
let [[x0,y0],[x1,y1],[x2,y2]] = ps;
return `M${x0} ${y0} Q${x1} ${y1} ${x2} ${y2}`;
}
/**
* Returns an SVG path string of a cubic bezier curve.
* @param ps The cubic bezier control points.
*/
function getCubicBezierPathStr(ps: number[][]) {
let [[x0,y0],[x1,y1],[x2,y2],[x3,y3]] = ps;
return `M${x0} ${y0} C${x1} ${y1} ${x2} ${y2} ${x3} ${y3}`;
}
/**
* The SVG path string representing our shape.
*/
const svgPathStr = `
M 144 251
C 145 169 110 82 227 59
C 344 36 429 -46 505 96
C 581 238 696 407 554 435
C 412 463 191 532 197 442
C 203 352 213 363 276 346
C 339 329 563 318 437 242
C 311 166 302 181 297 314
C 292 447 160 585 151 419
C 142 253 87.12 312.78 86 314
C 87.16 312.74 142.8632 252.2348 144 251
z
`;
/**
* Adds a path to the given SVG element and give it a shape-path class.
*/
function setSvgShapePath(
$svg: SVGSVGElement,
pathStr: string) {
let $path = document.createElementNS(NS, 'path'); // Create SVG path elem.
$path.setAttribute('class', 'shape-path');
$svg.appendChild($path); // Add the path element to the SVG.
document.body.appendChild($svg); // Add the SVG to the document body.
$path.setAttribute('d', svgPathStr);
}
function main() {
// Create and add and SVG element to our HTML page.
let $svg = createSvg(1); // Create SVG element.
setSvgShapePath($svg, svgPathStr);
// Get loops (representing the shape) from some SVG path.
let bezierLoops = getPathsFromStr(svgPathStr);
// We could also just give an array of linear, quadratic or cubic beziers as
// below (all lines in this case). Note that in the below case there is only
// one array of beziers (forming a single loop shape).
/*
bezierLoops = [
[
[[50.000, 95.000],[92.797, 63.905]],
[[92.797, 63.905],[76.450, 13.594]],
[[76.450, 13.594],[23.549, 13.594]],
[[23.549, 13.594],[7.202, 63.90]],
[[7.202, 63.900],[50.000, 95.000]]
]
];
*/
// Get MATs from the loops.
let mats = findMats(bezierLoops, 3);
// Draw the MATs.
drawMats(mats, $svg, 'mat');
// Get the SAT (at scale 1.5) of the MATs (of which there is only 1)
let sats = mats.map(mat => toScaleAxis(mat, 1.5));
drawMats(sats, $svg, 'sat');
}
/**
* Returns a function that draws an array of MAT curves on an SVG element.
* @param mats An array of MATs to draw.
* @param svg The SVG element on which to draw.
* @param type The type of MAT to draw. This simply affects the class on the
* path element.
*/
function drawMats(
mats: Mat[],
svg: SVGSVGElement,
type: string /* 'mat' | 'sat' */) {
mats.forEach(f);
/**
* Draws a MAT curve on an SVG element.
*/
function f(mat: Mat) {
let cpNode = mat.cpNode;
if (!cpNode) { return; }
let fs = [,,getLinePathStr, getQuadBezierPathStr, getCubicBezierPathStr];
traverseEdges(cpNode, function(cpNode) {
if (cpNode.isTerminating()) { return; }
let bezier = cpNode.matCurveToNextVertex;
if (!bezier) { return; }
let $path = document.createElementNS(NS, 'path');
$path.setAttributeNS(
null,
"d",
fs[bezier.length](bezier)
);
$path.setAttributeNS(null, "class", type);
svg.appendChild($path);
});
}
}
main();The first part of the code is just concerned with importing stuff. Then there is a function
for programatically creating an SVG HTML element. The next three functions, getLinePathStr,
getQuadBezierPathStr and getCubicBezierPathStr will be used for creating the paths that will
represent the Medial Axis on our SVG. Following that is the SVG path string of our shape and
a function, setSvgShapePath, to add the path to the SVG.
The next function, main, is the entry point of our example. The first two lines creates the
SVG and sets the path. The third line:
let bezierLoops = getPathsFromStr(svgPathStr);extracts the path data into an array that is suitable to be comsumed by findMats,
the function from the library that will do the number crunching and return an array
of Medial Axis Transforms. The array, bezierLoops is of type number[][][][].
It is an array of 'loops'. Each 'loop' (of which there is only one in our case) is a sequence of
bezier curves such that the starting point of the first bezier corresponds to the end point of
the last. Each bezier in the loop is represented by its (2, 3 or 4) control points which has type
signature number[][] hence the type number[][][][] for bezierLoops.
For example, the cubic bezier with control points at (1,1), (5,1), (5,2) and (4,2) is represented as
an array of points [[1,1],[5,1],[5,2],[4,2]]. A loop consisting of just 2 beziers can
be encoded as say [ [[1,1],[5,1],[5,2],[4,2]], [4,2],[3,3],[1,3],[1,1] ] and finally
we can make an array of loops from this (containing just 1 element) as follows:
[[ [[1,1],[5,1],[5,2],[4,2]], [4,2],[3,3],[1,3],[1,1] ]].
The reason for being able to provide an array of loops is because a shape might consist of an outer loop with one or more inner loops representing holes. This is also reflected in the fact that SVG paths can have sub-paths. In such a case the inner loops must have opposite orientation than the outer envelope loop. The rule used to indicate which loops form holes and which are part of the shape is the default SVG non-zero fill rule. Loops may also intersect each other, in the process possibly creating more than one disjoint shape. In the above example a single intersecting loop creates a shape with a hole.
This brings us to the heart of the example, the findMats function.
let mats = findMats(bezierLoops, 3);The function extracts the Medial Axis Transforms of all shapes created by the the array of input bezier loops. It takes an additional parameter indicating the number of points on each bezier for which a MAT vertex 'point' should be calculated. A value of 3 is the default and is a reasonable compromise between speed and accuracy. A value of 15 would give highly accurate results.
In the special case of a single non-intersecting closed loop the returned MAT array will be of length 1. Let us look at it in more detail.
The returned MAT is essentially a tree data structure. Even if the shape contains holes it is a tree since the graph is snipped at so-called hole-closing maximal disks to form a tree. (It is still possible though to traverse the MAT as a non-tree graph if required).
As in the example code above, we can traverse the tree to
draw the Medial Axis (MA). This is done by utilizing the traverseEdges function. (Note that
the MA is the MAT but without the maximal disk radius, etc. information encoded on
it). This is accomplished by the drawMats function. The inner function, f,
draws a single MA.
First we select a tree node as the root of
the MAT tree. One such node is given to us via mat.cpNode.
The tree can now be traversed from this node outwards to the tree
leaves just like in any other tree traversal. Each node, which is
a class of type CpNode (for Contact Point Node), has several
properties (see the docs). For our current purposes
we only need the matCurveToNextVertex property.
matCurveToNextVertex is a bezier curve (as defined previously with
type number[][]) of order 1, 2 or 3 forming a part of
the MA. In the example code we draw this curve on our orignal SVG.
The main function concludes by finding the Scale Axis Transform of our found
MAT and then drawing it on top of the MAT with a different css class (blue).
Whether your target is Node or the browser the library can be installed via npm. (For the browser you can also download the minified .js file - see below)
So whatever your target, at the the command line:
npm install flo-mat --save
Node with JavaScript (or the browser (with webpack) or similar)
In your project
let FloMat = require("flo-mat");or if you only want to require specific functionality:
let { findMats } = require('flo-mat');In your project
import * as FloMat from "flo-mat";or for specific functionalities:
import { findMats } from "flo-mat";After the npm installation simply include the script in your project:
<script src='node_modules/flo-mat/browser/index.min.js'></script>A new global object will available called FloMat representing the library.
Please see the documentation for the primary functions and classes: findMats, toScaleAxis and CpNode.
For documentation and code examples please see the documentation
The MIT License (MIT)
Copyright © 2018 Floris Steenkamp
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.