Python3 TS demo, no any pip requirements.
- crypto.py, hash functions, base58check encoder and decoder
- meta.py, operations of bitcoin objects, such as
int_to_varint,serialize_public_key,public_key_to_address, etc. - modular_inverse.py, calculate the modular multiplicative inverse of integer
aunder modulon - ec_point_operation.py, points add and scalar multiply operations on Secp256k1 curve
- sign.py, ECDSA implementation, sign and verify ECDSA signature (r, s)
- sign_transaction.py, functions to sign a bitcoin transaction
- sign_message.py, use bitcoin private key to sign arbitrary message
- polynomial.py, implementation of polynomial
y = a0 * x^0 + a1 * x^1 + ... + at * x^ton finite field Secp256k1.n - threshold_signature.py, TS operations,
jvrss,addss,prossandinvss - ts_demo.py, a demo with detailed process logs
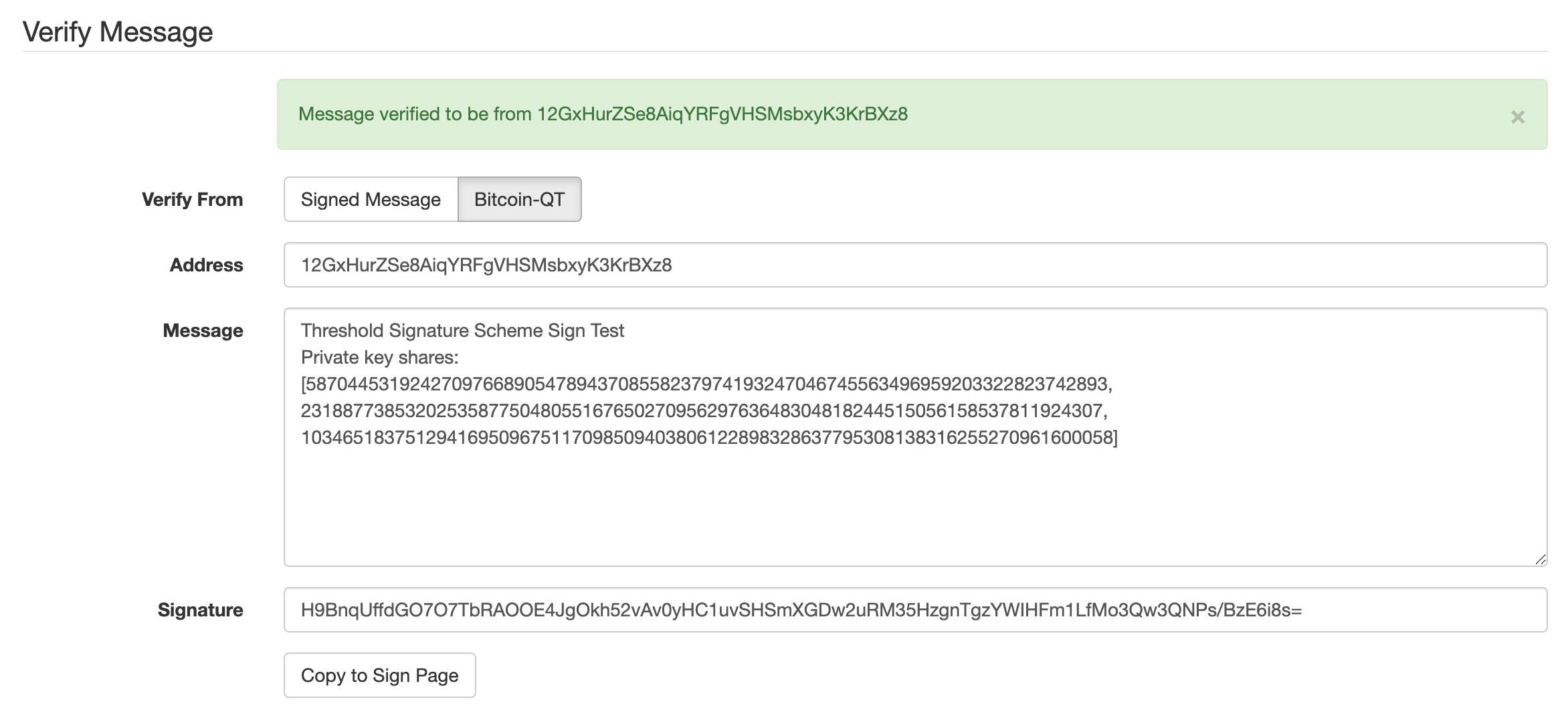
Threshold Signature Scheme Sign Test
Private key shares:
[58704453192427097668905478943708558237974193247046745563496959203322823742893, 23188773853202535877504805516765027095629763648304818244515056158537811924307, 103465183751294169509675117098509403806122898328637795308138316255270961600058]
------------------
12GxHurZSe8AiqYRFgVHSMsbxyK3KrBXz8 H9BnqUffdGO7O7TbRAOOE4JgOkh52vAv0yHC1uvSHSmXGDw2uRM35HzgnTgzYWIHFm1LfMo3Qw3QNPs/BzE6i8s=
------------------
True
Check outputs with online Bitcoin Signature Tool, great!
If specify debug = True, the polynomial will only random coefficients between 1 and 10, else between 1 and Secp256k1.n.
Run ts_demo.py.
---------------------- demo ----------------------
group size = 3
key threshold = 2
signature threshold = 3
polynomial order = 1
------------ jvrss ------------
Player 1 <Polynomial order=1, coefficients=[1, 4]>
Player 2 <Polynomial order=1, coefficients=[6, 3]>
Player 3 <Polynomial order=1, coefficients=[7, 8]>
f1(1) = 5 f1(2) = 9 f1(3) = 13
f2(1) = 9 f2(2) = 12 f2(3) = 15
f3(1) = 15 f3(2) = 23 f3(3) = 31
secret = 14
mod_inv_secret = 74437771652560411343724204648442226476824148465119581388817604876690246674931
public key = (33301309993451753050311554695703528430361259803437469669590207169100761277412, 91711666877231500617203373035680263572492971120307578300405368749466283229019)
shares = [29, 44, 59]
-------------------------------
shares = [29, 44, 59]
public_key = (33301309993451753050311554695703528430361259803437469669590207169100761277412, 91711666877231500617203373035680263572492971120307578300405368749466283229019)
restored key = 14
------------ jvrss ------------
Player 1 <Polynomial order=1, coefficients=[9, 7]>
Player 2 <Polynomial order=1, coefficients=[6, 8]>
Player 3 <Polynomial order=1, coefficients=[6, 5]>
f1(1) = 16 f1(2) = 23 f1(3) = 30
f2(1) = 14 f2(2) = 22 f2(3) = 30
f3(1) = 11 f3(2) = 16 f3(3) = 21
secret = 21
mod_inv_secret = 11027818022601542421292474762732181700270244217054752798343348870620777285175
public key = (24049875635381557237058143631624836741422505207761609709712554171343558302165, 22669890352939653242079781319904043788036611953081321775127194249638113810828)
shares = [41, 61, 81]
-------------------------------
another shares = [41, 61, 81]
------------ addss ------------
[29, 44, 59]
[41, 61, 81]
shares addition = [70, 105, 140]
points picked = [(1, 70), (3, 140)]
secrets addition = 35
-------------------------------
shares addition = 35
------------ pross ------------
[29, 44, 59]
[41, 61, 81]
shares product = [1189, 2684, 4779]
points picked = [(3, 4779), (1, 1189), (2, 2684)]
secrets product = 294
-------------------------------
shares product = 294
------------ invss ------------
[29, 44, 59]
------------ jvrss ------------
Player 1 <Polynomial order=1, coefficients=[4, 4]>
Player 2 <Polynomial order=1, coefficients=[8, 7]>
Player 3 <Polynomial order=1, coefficients=[1, 7]>
f1(1) = 8 f1(2) = 12 f1(3) = 16
f2(1) = 15 f2(2) = 22 f2(3) = 29
f3(1) = 8 f3(2) = 15 f3(3) = 22
secret = 13
mod_inv_secret = 8907083787485861186428537308360608296372120329159608029431166395501397038026
public key = (109699032664856045668214896063362497021339186688470416858630178803463338613416, 4835088675770141268294878046681321747490758260515711581034896622314066275713)
shares = [31, 49, 67]
-------------------------------
------------ pross ------------
[29, 44, 59]
[31, 49, 67]
shares product = [899, 2156, 3953]
points picked = [(2, 2156), (3, 3953), (1, 899)]
secrets product = 182
-------------------------------
u = 182
mod_inv_u = 50261401372241645266275317668606289672385536143114931023218724660329311857432
inverse shares = [52806282454380462748112042613852177757063284808589104745913343630472568154011, 31174793256200514152499880579262129037302421152058628103009082384254889633091, 9543304058020565556887718544672080317541557495528151460104821138037211112171]
points picked = [(2, 31174793256200514152499880579262129037302421152058628103009082384254889633091), (1, 52806282454380462748112042613852177757063284808589104745913343630472568154011), (3, 9543304058020565556887718544672080317541557495528151460104821138037211112171)]
inverse secret = 74437771652560411343724204648442226476824148465119581388817604876690246674931
-------------------------------
inverse shares = [52806282454380462748112042613852177757063284808589104745913343630472568154011, 31174793256200514152499880579262129037302421152058628103009082384254889633091, 9543304058020565556887718544672080317541557495528151460104821138037211112171]
--------------------------------------------------
- Threshold Signature Paper of nChain
- AustEcon/bitsv