-
Usage
foo@bar:~$ python quench_dynamics_1d_FM_TFIsing.py -N [system size]
Model: H(t) = - (\sum_{i} \sigma_i^z \sigma_{i+1}^z + h(t) \sum_{i} \sigma_i^x)
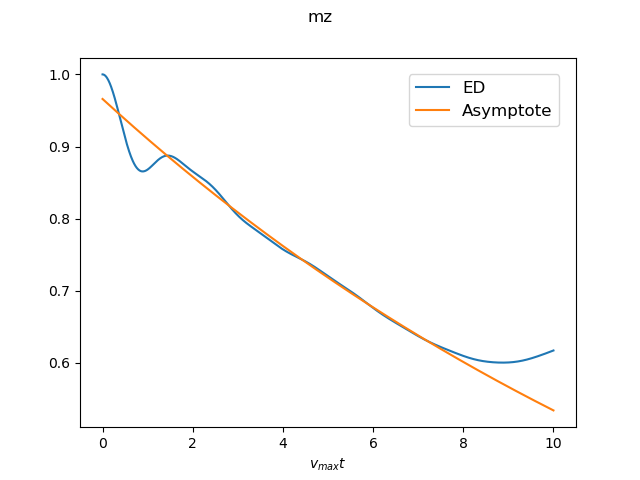
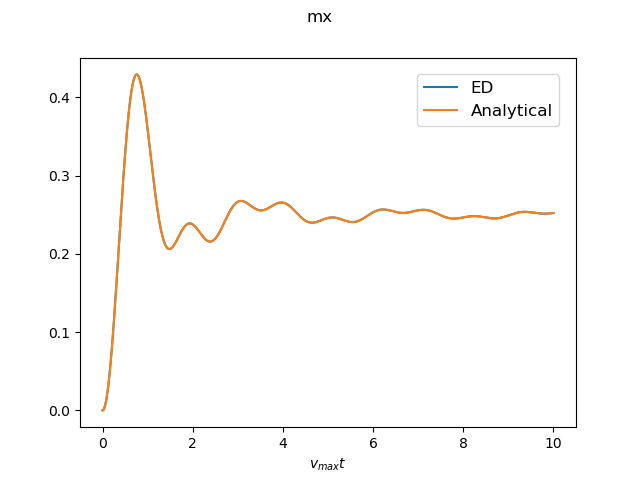
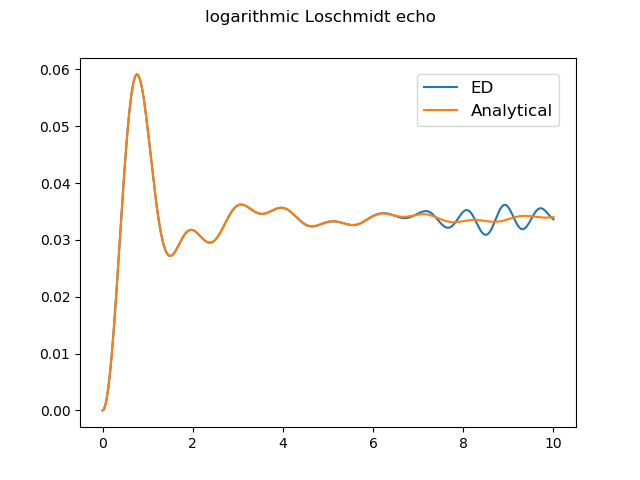
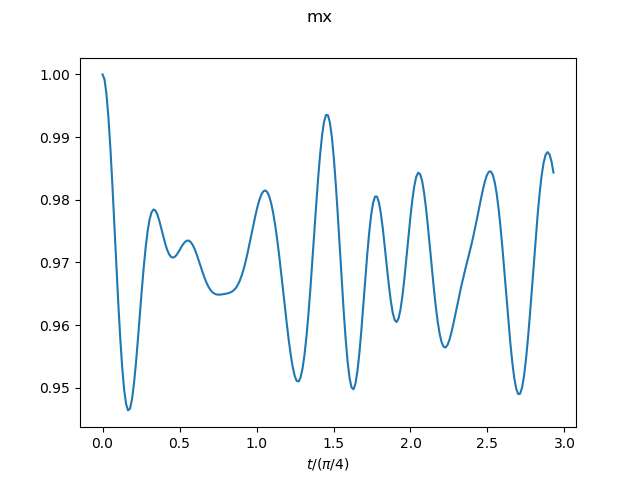
Field: h(t=0)=0 (Ising GS: all up) --> h(t>0)=0.5
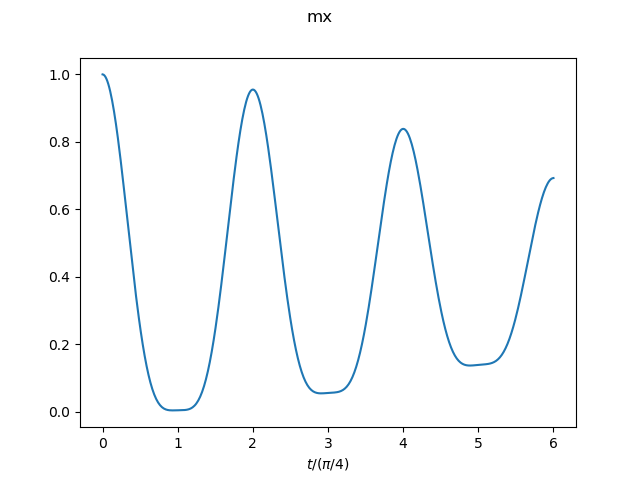
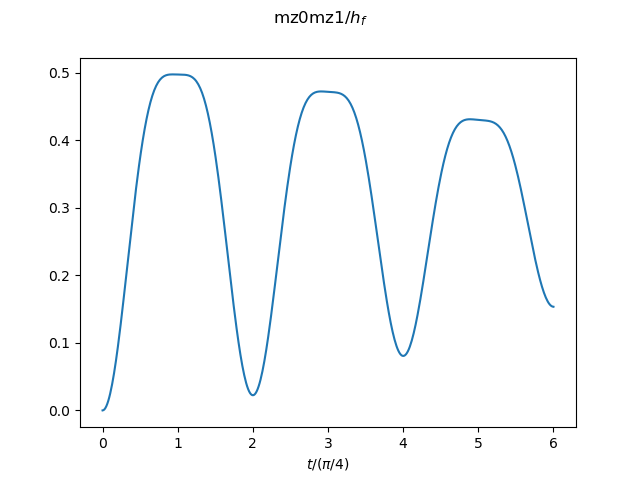
The result for the system size N=16 is shown as an example. -
References
- https://doi.org/10.1103/PhysRevA.2.1075
- https://doi.org/10.1103/PhysRevA.3.786
- https://doi.org/10.1103/PhysRevA.3.2137
- https://doi.org/10.1103/PhysRevLett.106.227203
- https://doi.org/10.1088/1742-5468/2012/07/P07016
- https://doi.org/10.1088/1742-5468/2012/07/P07022
- https://doi.org/10.1007/978-3-642-33039-1
- https://amslaurea.unibo.it/id/eprint/15866 (I followed this notation.)
- https://arxiv.org/abs/2005.03104 (numerical linked cluster expansion + forward propagation of pure states)
- https://doi.org/10.1088/1742-5468/2016/06/064007 (long time limit)
-
Results
- Analitycal and asymptotic results in the thermodynamic limit are also given.
-
Usage
foo@bar:~$ python quench_dynamics_1d_FM_TFIsing.py -N [system size]
Model: H(t) = - (\sum_{i} \sigma_i^z \sigma_{i+1}^z + h(t) \sum_{i} \sigma_i^x)
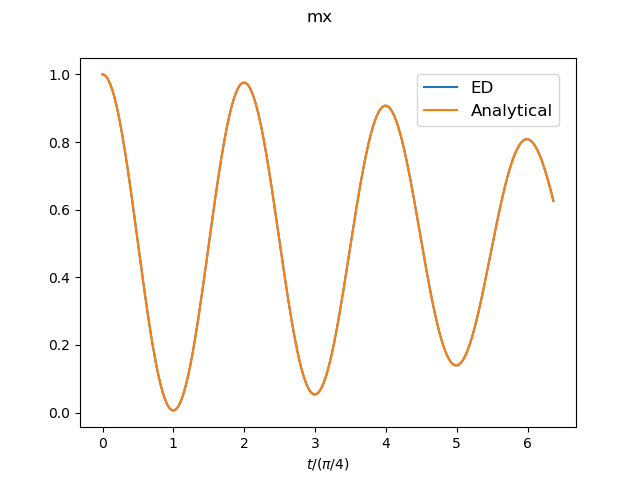
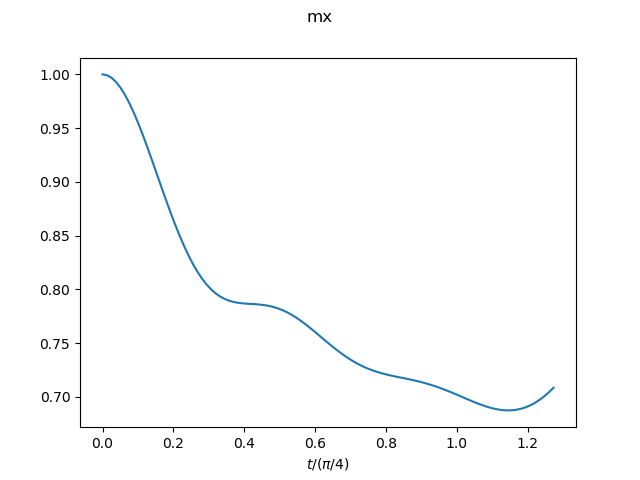
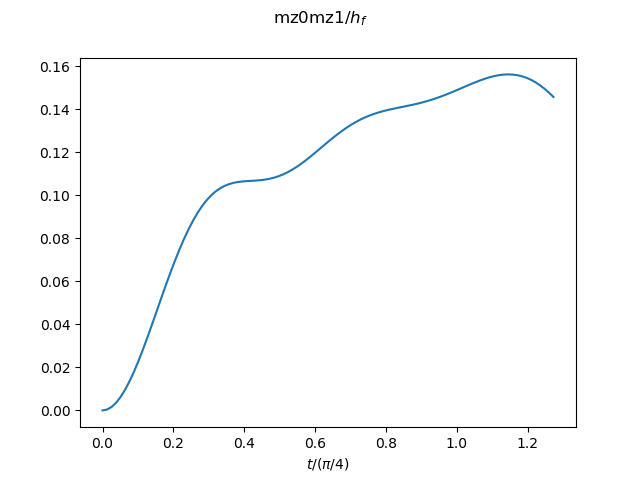
Field: h(t=0)=inf --> h(t>0)=0.1
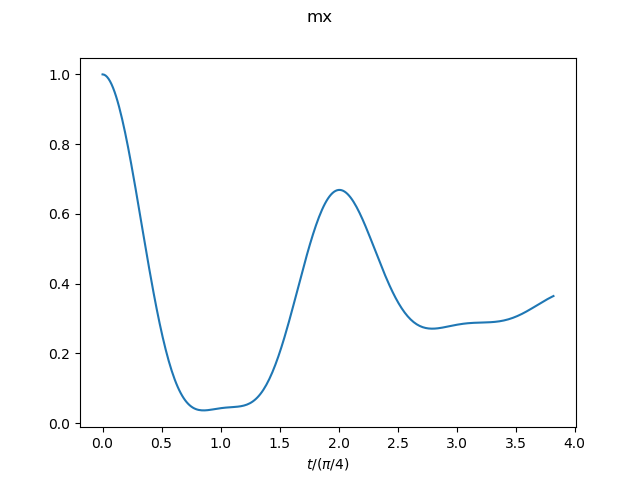
The result for the system size N=10 is shown as an example. -
References
- https://doi.org/10.21468/SciPostPhys.4.2.013 (See Fig.2 for comparison, note that h'/J'=0.05 <--> h/J=0.1 where J'/4=J and h'/2=h)
-
Results
-
Usage
foo@bar:~$ python slow_dynamics_1d_FM_TFIsing.py -N [system size] -tau [total time]
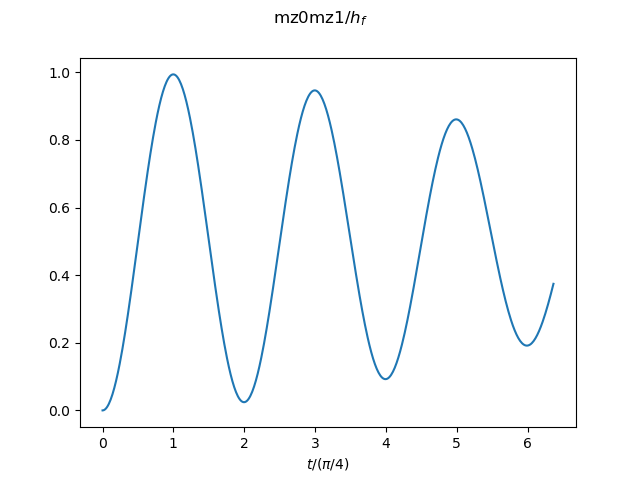
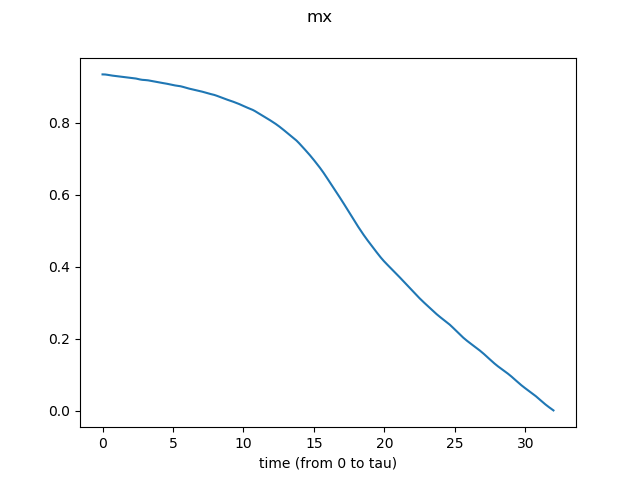
Model: H(t) = - (\sum_{i} \sigma_i^z \sigma_{i+1}^z + h(t) \sum_{i} \sigma_i^x)
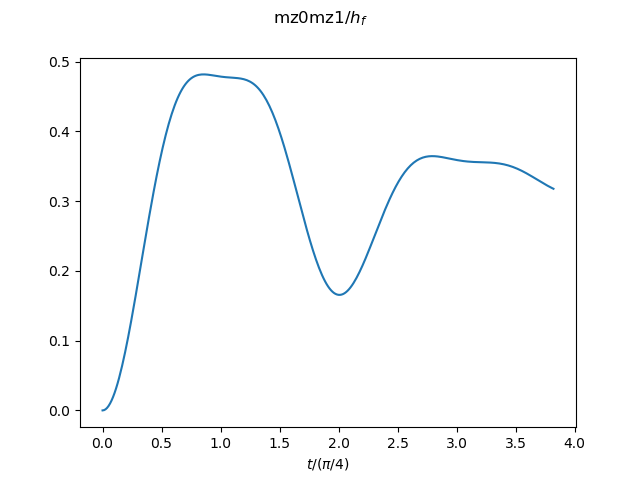
Field: h(t)=hi+(hf-hi)*t/tau (hi=2*hc, hf=0, hc=1)
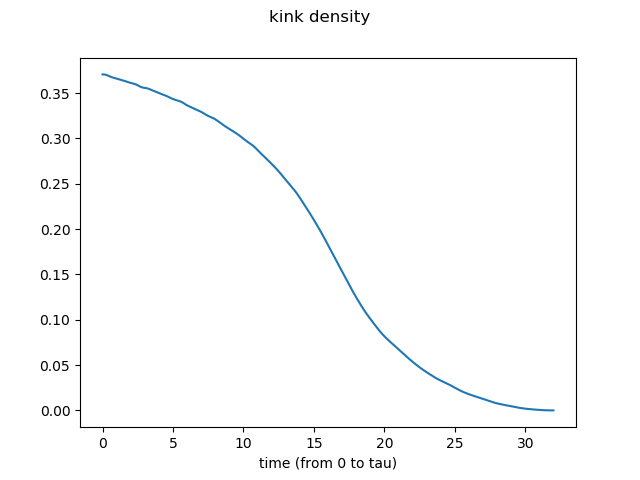
The result for the system size N=10 and the total time tau=32 is shown as an example. -
References
- https://doi.org/10.1103/PhysRevLett.95.035701
- https://doi.org/10.1103/PhysRevLett.95.105701
- https://doi.org/10.1103/PhysRevLett.95.245701
- https://doi.org/10.1103/PhysRevB.72.161201
- https://doi.org/10.21468/SciPostPhys.1.1.003
- https://doi.org/10.1080/00018732.2010.514702
- https://doi.org/10.1007/978-3-642-33039-1
- https://doi.org/10.1088/1367-2630/aa65bc
- https://people.mines.edu/lcarr/wp-content/uploads/sites/23/2018/11/jaschke_thesis_2018.pdf
- https://doi.org/10.1088/1742-5468/2016/06/064007 (long time limit)
-
Results
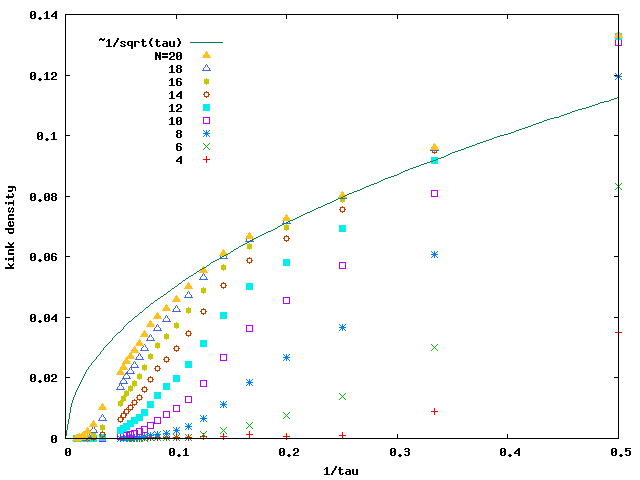
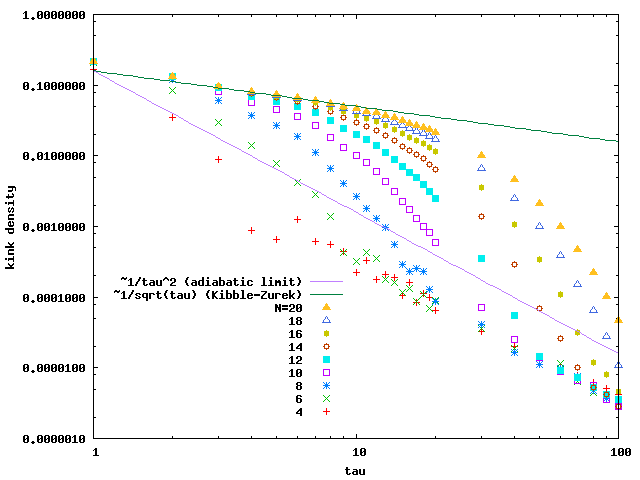
- The kink density at the final time (t=tau) is expected to be scaled as (kink density)~1/(tau)^0.5 in the thermodynamic limit.
-
Usage
foo@bar:~$ python quench_dynamics_2d_FM_TFIsing.py -Lx [size Lx] -Ly [size Ly] -hi [initial field] -hf [final field] -tau [total time]
Model: H(t) = - (\sum_{i} \sigma_i^z \sigma_{i+1}^z + h(t) \sum_{i} \sigma_i^x)
Field: h(t=0)=inf --> h(t>0)=0.1, hc/10, hc, 2*hc (hc=3.04438)
The result for the system size N=4x4 is shown as an example. -
References (h(t=0)=inf --> h(t>0)=0.1)
- https://doi.org/10.21468/SciPostPhys.4.2.013 (See Fig.2 for comparison, note that h'/J'=0.05 <--> h/J=0.1 where J'/4=J and h'/2=h) (neural networks)
-
References (h(t=0)=inf --> h(t>0)=hc/10, hc, 2*hc (hc=3.04438))
- https://doi.org/10.1103/PhysRevB.99.035115 (iPEPS)
- https://arxiv.org/abs/1912.08828 (neural networks, comparison with iPEPS)
- https://arxiv.org/abs/2005.03104 (numerical linked cluster expansion + forward propagation of pure states)
-
Other references
- https://doi.org/10.1038/srep38185 (VMC)
- https://arxiv.org/abs/1710.07696 (numerical linked cluster expansion)
- https://arxiv.org/abs/1811.09275 (MPS)
- https://arxiv.org/abs/1910.10726 (MPS, triangular TFI)
- https://arxiv.org/abs/1912.08831 (neural networks, time evolution error)
- (https://doi.org/10.21468/SciPostPhys.6.3.031 (iPEPS, Heisenberg+field))
- (https://doi.org/10.21468/SciPostPhys.8.2.021 (iPEPS, t-J))
-
Results (h(t=0)=inf --> h(t>0)=0.1)
- Results (h(t=0)=inf --> h(t>0)=hc/10 (hc=3.04438))
- Results (h(t=0)=inf --> h(t>0)=hc (hc=3.04438))
- Results (h(t=0)=inf --> h(t>0)=2*hc (hc=3.04438))
-
Usage
foo@bar:~$ python slow_dynamics_2d_FM_TFIsing.py -Lx [size Lx] -Ly [size Ly] -hi [initial field] -hf [final field] -tau [total time]
Model: H(t) = - (\sum_{i} \sigma_i^z \sigma_{i+1}^z + h(t) \sum_{i} \sigma_i^x)
Field: h(t)=hi+(hf-hi)*t/tau (hi=2*hc, hf=0, hc=3.04438)
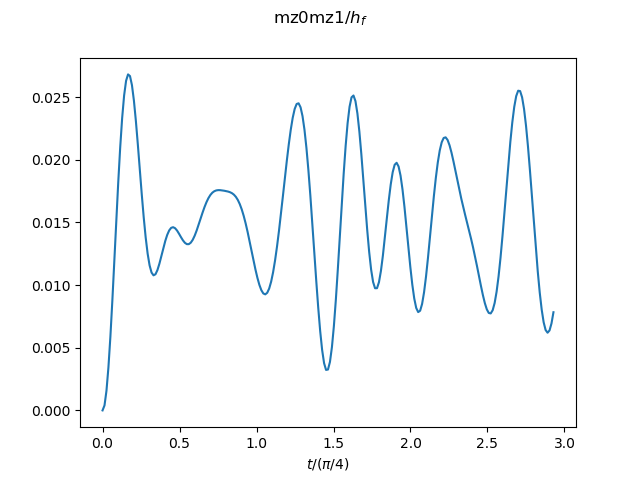
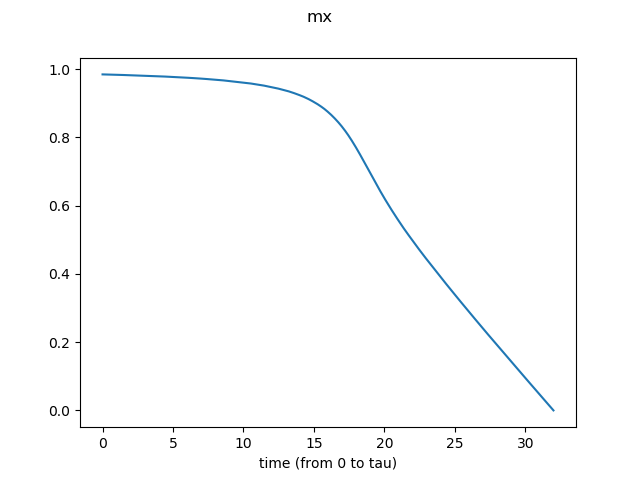
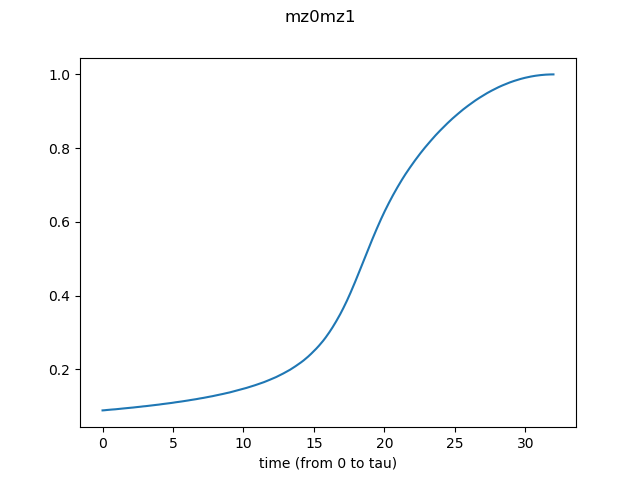
The result for the system size N=4x4 and the total time tau=32 is shown as an example. -
Related references
- Kibble-Zurek
- dynamics by QMC (real time dynamics ~ imaginary time dynamics when v=1/tau << 1)
- QA
- https://arxiv.org/abs/2001.11637 (scaling in D-dimensions: kink density, higher order cumulants: see references therein)
- http://hdl.handle.net/2433/142655
- http://hdl.handle.net/2433/110379 (scaling of residual energy)
- https://www.smapip.is.tohoku.ac.jp/~dex-smi/2006/Workshop200612/ExtendedAbstracts/SeiSuzuki.pdf
-
Results