This code analyzes a library of audio samples and determines each sample's tempo, tuning, and harmonic profile. Using these values we determine pairs of samples that, when played at particular speeds, have the same tempo, have the same tuning and are harmonically coherent. It is intended as a compositional tool for making sample-based music.
The sampling technique this work serves to aid is sometimes known as "plunderphonics" or a "sound collage". It was popularized by The Avalanches in their masterpiece Since I Left You. This technique involves layering many samples on top of each other. DJs employ a related technique called harmonic mixing to transition smoothly between different songs. Even though the samples are often untouched (no chopping or added effects), the combination of different moods and genres and in which they are placed creates an entirely new sound. There is something incredibly moving and surreal in being able to take recordings from different genres, different decades, and different continents and realizing them as different parts of the same song.
Despite its beauty, music made with this technique is rare, perhaps because of how difficult it is to create; the process of finding groups of samples that can be played simultaneously is extremely time consuming. This is partly because two fundamental musical properties, tempo and pitch, are inherently linked. Lowering or raising the pitch of a song slows down or speeds up the tempo. If two samples do in fact have the same tempo and tuning (tuning measured in cents as the deviation from 12-tone equal tempermant with A4 = 440hz), they might not be harmonically coherent. For example the samples could be in conflicting keys or modes, again greatly reducing the number valid sample pairs. Once a musician has finally found samples that have consistent rhythm, tuning and harmony, they then get to choose which samples should actually go together based on aesthetics and composition.
It should be noted that a process called time stretching is able to change the speed of audio without affecting the pitch. However it necessitates windowing the audio which introduces digital artifacts particularly at transients. Modern algorithms cover up most of these artifacts, but there is nevertheless something uncanny about time-stretched audio even for small changes in speed. Even more advanced algorithm's like the technology that exists in the commericial software Melodyne allow for the pitches of individual notes within a single audio sample to be modified independenly; changing the internal harmony. But once again this can cause harsh digital artifacts.
This code works to make the sampling process easier by automatically detecting pairs of samples that can be played at the same time and still sound "musical".
I have a collection of audio samples in Ableton's *.alc file format (a convenient way to make references to sections of audio). These are small (~3-30s long) snippets of music from a variety of genres; soul, jazz, funk, rock, hip-hop, disco, electronic, experimental, etc. My own collection is not public due to copyright, but there is a large online database of the samples used in popular music at WhoSampled.com
Each of these samples is analyzed using spectral analysis to determine it's tempo, tuning and harmonic profile. The harmonic profile encodes how prevalent each of the 12 notes is in the sample. Since there is a closed-form relation between tempo and pitch, we can easily determine which pairs of samples can be repitched to have the same tempo and still be in tune. A song with tempo
needs to be retuned by
cents in order to have tempo
:
So long as the tuning is approximately an integer number of semitones, then the pair is "in tune."
The harmonic profiles of these tuned sample pairs are combined and fed into a classifier which rates them based on how harmonically coherent they are. For example a profile which is dominated by the notes "C" "E" and "G" (a major chord) would be labeled "coherent", where as a profile where all the notes have equal weight would be labeled "incoherent". The classifier, which is a fully connected neural network, is trained on the sample collection itself using positive unlabeled learning.
A large amount of signal processing is done on the audio signal to determine a compressed representation encapsulating tempo, tuning and harmony. As an example of the techniques used we will use the following audio clip.
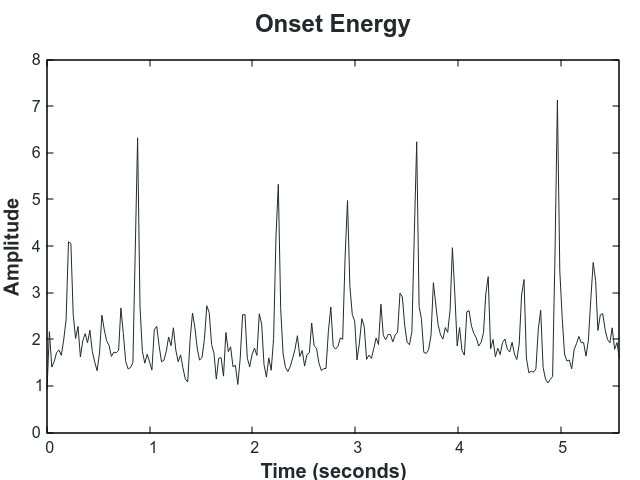
To detect the tempo we first compute the onsets of the audio using the complex-domain method described in On the Use of Phase and Energy for Musical Onset Detection in the Complex Domain. The onset signal is high when there are changes in amplitude or frequency, which typically represent beats:
We then take the autocorrelation of the onset signal which reveals the periodic signal in the onsets:
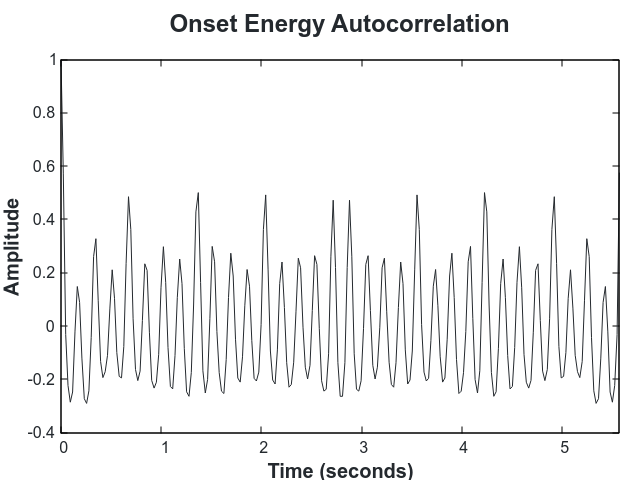
The fourier transform of the autocorrelation is peaked around the tempo! We find the peak using the algorithm described in Estimation of Frequency, Amplitude, and Phase from the DFT of a Time Series:

We then fine tune the peak tempo by iterating over a small window around that value.
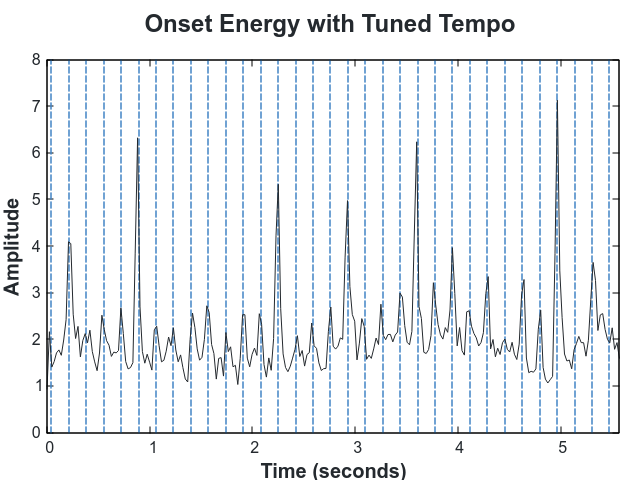
In each iteration we perform a weighted sum of the onsets. The weights are low close to each beat, as determined by the tempo in that particular iteration (marked in blue below), and high away from them.
By choosing the tempo that minimizes that sum, the tempo very clearly aligns with the onsets.
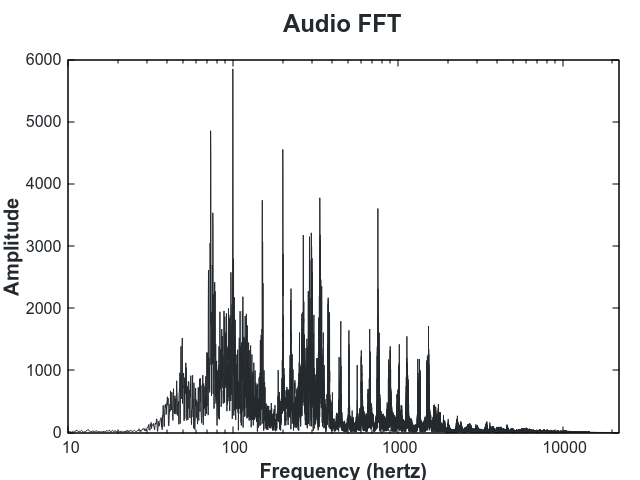
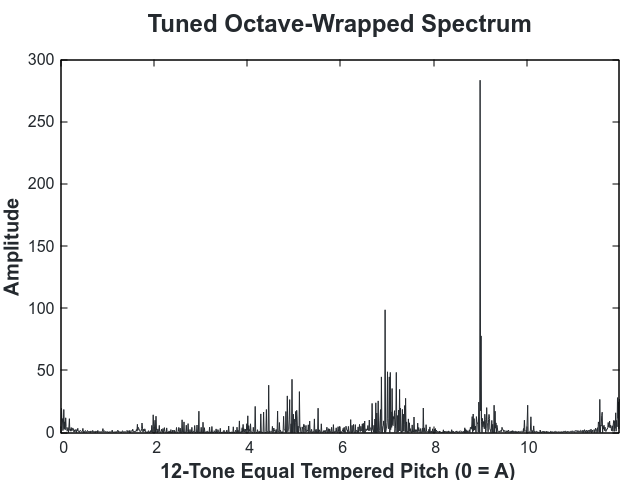
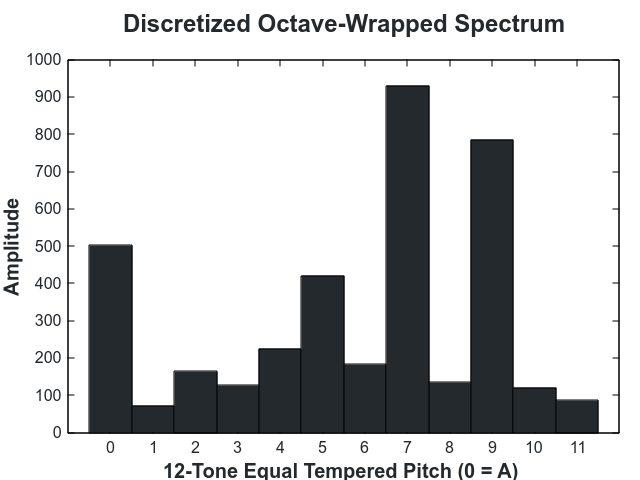
The harmonic profile we use is the spectrum of the audio, wrapped to an octave and discretized into 12 notes. To compute it we first compute the FFT:
Then we filter the audio using an https://en.wikipedia.org/wiki/A-weighting curve. This attenuates the frequnecies to match the frequncy response of the human ear. Low frequences (< 1kHz) and high frequences (> 10kHz) are reduced and frequnceis in the talking range (~2kHz) are most pronounced.
We then use the peak picking described in Estimation of Frequency, Amplitude, and Phase from the DFT of a Time Series and accumulate these peaks in a histogram with the frequencies wrapped to an octave. Since the frequency doubles in each octave, the placement in the octave on a scale from 0 to 1 is:
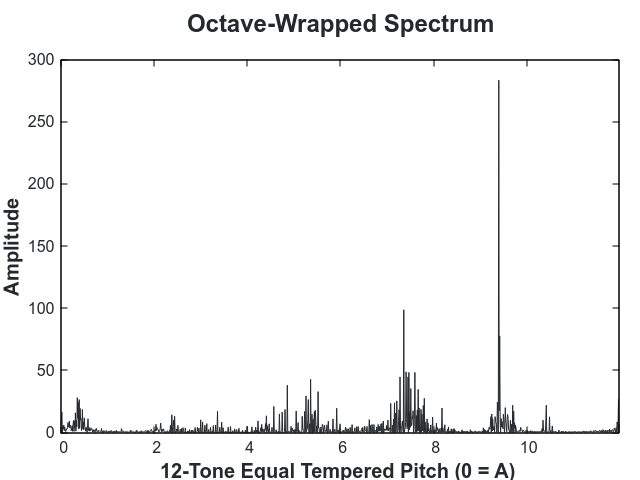
On a scale from 0 to 11 (the 12 notes in an octave), our octave looks like:
The above octave is out of tune. This is visible due to the fact that the peaks are shifted away from an integer bin. To tune, we then find the number of cents that minimizes the distance of the weight in the histogram from an integer bin.
After the octave is tuned it is discretized to produce a 12-value profile:
Using the octave-mapped spectrogram as a compact profile of a sample's harmonic content, we can now classify pairs of samples as being harmonic or inharmonic. While throughout history many "rules of harmony" have been proposed, those rules are often broken and change over time. Moreover they would be extremely difficult to impliment consistently. Instead we take advantage of the fact that we already have a dataset of samples which are "harmonic".
Using this dataset, classifying pairs of samples as harmonic is a positive-unlabeled learning problem. All of the samples in the dataset are considered to be harmonic examples and we can combine any pair of these samples to create an unlabeled example.
We use a multilayer fully connected neural network to fit train. Since the network has so many free parameters, PU-learning is prone to overfit so we use a non-negative loss function via Positive Unlabeled Learning with Non-Negative Risk Estimator.
In addition we normalize all the inputs, add batch normalization, and dropout to prevent overfitting. We also augment the data by rotating the octaves uniformly at random. To have better rotational invariance we use a variant of the layer decribed in Spatial Transformer Networks.
- Add quantitative values.
- Make a GUI.
- Using a recurrent neural network.
- Cmake
- ffmpeg
- tinyxml2
- fftw3
- boost