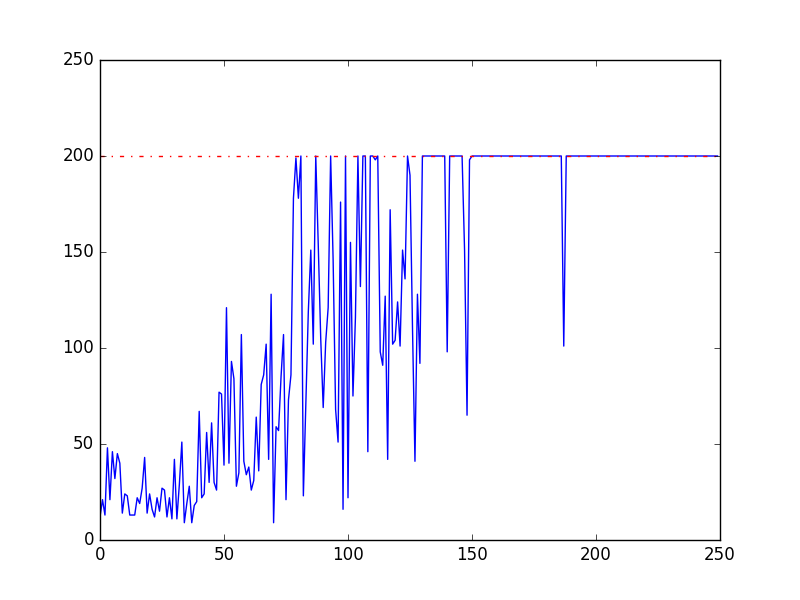
This is the experimental code of the non-parametric reinforcement learning with respect to the discrete state space and the discrete action space.
The agent accepts ANY form of the action and the state representation as inputs (string, vector, and so on 😄: NOTE: currrently a vector action have to be given as a string. The string is one of the universal interface 😅). If the environment is a finite-state MDP (explicitly or implicitly), implemented algorithms shoud find an appropriate solution (from the implication of the convergence theorem of RL algorithms 📖).
- Algorithms
- Q-Learning
- TD-Learning (without eligibility trace)
- Simple Model-based RL agent
- numpy
- graphviz (to visualize the model in the model-based agent)
- matplotlib, gym (to run example codes)
cd nonpara_discrete_rl
python setup.py installfrom nprl import QLearning
# Initialization
qlean = QLearning(initial_q_value=0.0,
exploration_rate=1.0,
lr=0.01,
discount_factor=0.5,
initial_fluctuation=True)
# Step Update
action = qlean.step(new_state=state,
reward=reward,
terminal=terminal,
action_list=action_list) # actions at current state
# Print Action-Value
print qlean.get_q_value()Please see /example for more detail
The code can be found in /example/model_based_gym.py.
Usually the implementation of RL algorithms with table representations are started with the definition of the Q-table with given state and action space size (|S| and |A|). I remember that I wrote those definition when I implemented the first Q-Learning experiment in my computer 💻
Usually agents do not know |S| and |A| in advance, but the naiive table implementation requires these values. The reinforcement learning theory (for finite-state MDP) requires the finiteness of states and actions of environment, but it is not necessarily explicit for agents. So this is a prior knowledge for the agent. In this time, I implemented RL algorithms to remove this requirement 👍
I think this is an implementation of a kind of the kernel-based reinforcement learning, more sophisticated non-parametric RL algorithms (like Pritzel (2017), Engel (2005)) will be preferred for more complex environment (like visual navigation tasks). Although this implementation only supports classic RL algorithms, this experience has deepen my understnding of the connection between the table-based RL, the kernel-based RL and the deep RL 😊
LICENSE : MIT