最良優先探索と深層学習でルービック・キューブを解いてみた

「勝手に最良優先探索とビーム・サーチでWater Jug Problemを解き直してみた」の続編です。今回は、探索アルゴリズムをマスターしていれば、あとは簡単なコピー＆ペーストでルービック・キューブのような難易度が高い問題を解けちゃうんだぜってのをやります。

といっても、解法は私のオリジナルではなく、カリフォルニア大学アーバイン校のDeepCubeAです。その昔、AlphaZeroを見たときもあまりに単純なので驚いたのですけど、DeepCubeAも単純（もちろん褒め言葉）で面白いですよ。

実行方法

作成したプログラムはGitHubにあります。NVIDIAのGPUを持っている方は、以下の手順で実行してみてください（GPUがない場合は、5を飛ばして実行してみてください）。

1. 未インストールなら、PythonとTensorflowとCUDAをセットアップする。
2. git clone https://github.com/tail-island/rubic-cube.git
3. cd rubic-cube
4. git lfs pull
5. model/cost.h5を削除してpython train-all.pyして、10日くらい待つ。結果だけ見たい場合は、このステップは飛ばしてください。
6. python solve.pyして、ルービック・キューブの問題と解答が出力されるのを見る。
7. Webブラウザでtest-ui/test-ui.htmlを開いて、6で出力された問題と解答を入力して、解答が正しいことを確認する。

最良優先探索やビーム・サーチの問題

前回の投稿を見ていただければ分かるのですけど、最良優先探索やビーム・サーチそのものはとても簡単です。コード小さいですし。

でも、最良優先探索やビーム・サーチ向けの評価関数を作ることは、とても難しいんですよ……。たとえば、将棋や囲碁の盤面の良さを測る評価関数を作るなんてのは、人間（少なくとも私）には不可能です。ルービック・キューブ用の評価関数も同様で、私ごときではどうにも作成できません。でも、評価関数がないと、最良優先探索もビーム・サーチもできません。どうしましょう……。

解決策。深層学習で評価関数を作っちゃえ！

まぁ、人間にできないなら、機械にやらせればよいだけなんだけどね。深層学習で、機械に評価関数を作らせちゃいましょう。

ただ、深層学習というのは入力と正解のペアを大量にぶち込んで入力と出力の関係のパターンを機械に導かせるという手法なので、どうにかして大量の入力と正解のペアを作らなければなりません。囲碁や将棋やATARIのゲームの場合は、実際にゲームをやらせてその結果をフィードバックする形でデータを作るみたいだけど（AlphaZeroやDQN）、ルービック・キューブの場合にはもっと簡単な方法があります。

考えてみましょう。最良優先探索やビーム・サーチで必要なのは、ゴールまでのコストを予測する評価関数です。今回の題材のルービック・キューブなら、あと何回まわせば6面揃うのかを予測する関数となるので、深層学習への入力データはルービック・キューブの状態、正解データはあと何回まわせば6面揃うのかの数値になるわけ。

で、これを逆にして、6面が揃った状態からたとえば3回適当にまわして、正解＝3、入力＝3回適当に回した結果とすれば、ほら、いくらでも無限にデータを作れちゃう！

実際に深層学習で評価関数を作ってみる

というわけで、実際にやってみましょう。まずは、ルービック・キューブのルールを実装します。あまり重要ではないので解説は省略しますけど、NumPyを使ったらとても楽ちんでした。詳細を知りたい場合はgame.pyを参照してください。

次に、深層学習のニューラル・ネットワーク……なのですけど、論文を斜め読みしたらResNetだと書かれていたので、昔書いたコードからコピー＆ペーストして作りました。結果はこんな感じ。

import tensorflow as tf

from funcy   import *
from game    import *
from pathlib import *


def computational_graph():
    def add():
        return tf.keras.layers.Add()

    def batch_normalization():
        return tf.keras.layers.BatchNormalization()

    def conv(filter_size, kernel_size=3):
        return tf.keras.layers.Conv2D(filter_size, kernel_size, padding='same', use_bias=False, kernel_initializer='he_normal')

    def dense(unit_size):
        return tf.keras.layers.Dense(unit_size, use_bias=False, kernel_initializer='he_normal')

    def global_average_pooling():
        return tf.keras.layers.GlobalAveragePooling2D()

    def relu():
        return tf.keras.layers.ReLU()

    ####

    def residual_block(width):
        return rcompose(ljuxt(rcompose(batch_normalization(),
                                       conv(width),
                                       batch_normalization(),
                                       relu(),
                                       conv(width),
                                       batch_normalization()),
                              identity),
                        add())

    W = 1024
    H =    4

    return rcompose(conv(W, 1),
                    rcompose(*repeatedly(partial(residual_block, W), H)),
                    global_average_pooling(),
                    dense(1),
                    relu())  # マイナスの値が出ると面倒な気がするので、ReLUしてみました。

論文中にregularizationは使わなかったと書かれていたのでkernel_regularizerの記述を消して、あとは入力が小さいのでプーリングを削って、最後をdense(1), relu()にしたくらいですな。脳を一切使わない機械作業で、とにかく楽ちん。そうそう、こんな単純なコードでニューラル・ネットワークを定義できる秘密は、Kerasと関数型プログラミングがスゴイおかげです。

で、このニューラル・ネットワークへの入力の型は、3×3×36の行列にしました。行列というと難しく感じますけど、実は3×3のモノクロ画像を36枚というだけの意味なのでとても簡単です。ルービック・キューブを見てみると、3×3の面が6個あるでしょ？　で、深層学習では赤を1で青を2とかで表現することはできない（青は赤の2倍という関係があるなら赤=1で青=2としてもいいのですけど、ルービック・キューブではそんな関係はない）ので、赤専用の3×3のモノクロ画像（赤ければ1で、そうでなければ0にします）を6面分、青専用の3×3のモノクロ画像を6面分という形で表現しなければならなくて、だから、3×3×（6面×6色）で3×3×36の行列になったというわけ。ニューラル・ネットワークへの入力形式への変換は、game.pyのget_x()関数で実施しています。名前がxとなっているのは、Tensorflowが採用している便利ライブラリのKerasには入力をxにして出力をyにするという習慣があるからです。

準備が整ったので、実際に訓練しましょう。これも、昔書いたコードからコピー＆ペーストして少し修正しただけです。

def main():
    def create_model():
        result = tf.keras.Model(*juxt(identity, computational_graph())(tf.keras.Input(shape=(3, 3, 6 * 6))))

        result.compile(optimizer='adam', loss='mean_squared_error', metrics=['mean_absolute_error'])
        result.summary()

        return result

    def create_generator(batch_size):
        while True:
            xs = []
            ys = []

            for i in range(batch_size):
                step = randrange(1, 32)

                xs.append(get_x(get_random_state(step)[0]))
                ys.append(step)

            yield np.array(xs), np.array(ys)

    model_path = Path('./model/cost.h5')

    model = create_model() if not model_path.exists() else tf.keras.models.load_model(model_path)
    model.fit_generator(create_generator(1000), steps_per_epoch=1000, epochs=100)

    model_path.parent.mkdir(exist_ok=True)
    tf.keras.models.save_model(model, 'model/cost.h5')

    tf.keras.backend.clear_session()

今回はデータをその場で生成できますから、Kerasのサンプルでよく見るmodel.fit()ではなく、model.fit_generator()を使用します。fit_generator()の引数はcreate_generator()関数の戻り値で、これは、データを生成する関数を返す関数です。create_generator()が返す関数では、まわす回数をランダムに選んで、その回数ランダムにまわした結果をxに、回数をyにしているだけです。

これを、model.fit_generator()の引数のように、1,000×1,000×100回の1億回繰り返してみます。論文には10 billion（100億）と書いてあったのでこれでは少ないかもしれませんから、train-all.pyで、この処理を10回繰り返して10億件のデータで学習させてみました。私が持っている型落ちのGPU（GeForce 1080 Ti）だと、学習に10日くらいかかって辛かったです……。

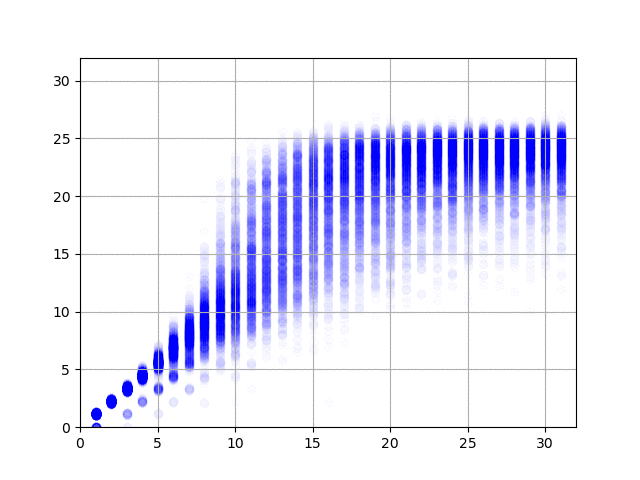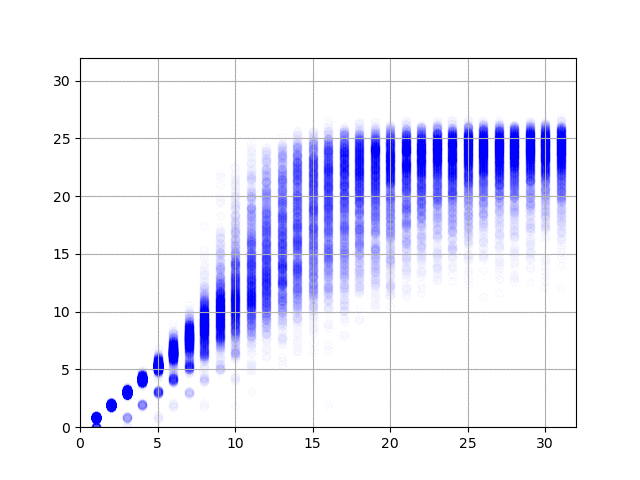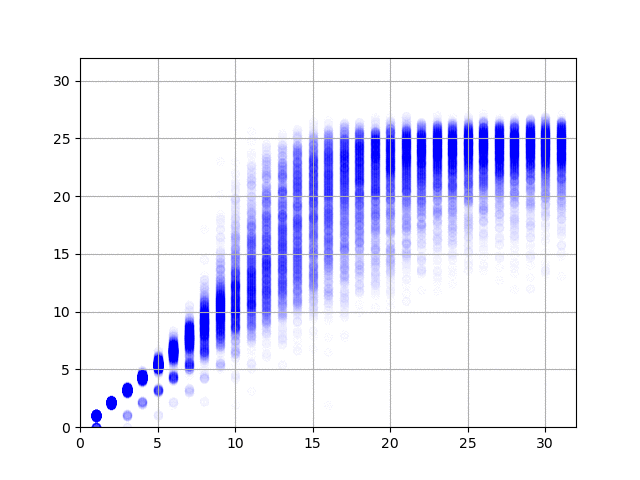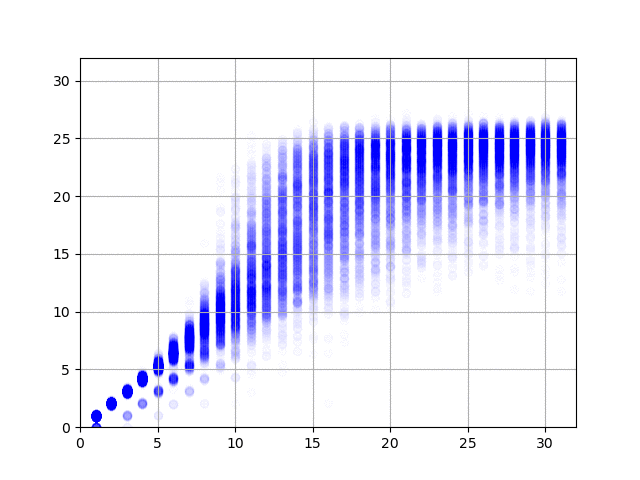
で、学習の結果を可視化してみると、以下の図のようになりました。横軸が正解データ（何回まわしたか）で、縦軸がニューラル・ネットワークからの出力です。1億件の結果、2億件の結果……と順にアニメーションします。

データの作り方がデタラメなので、たとえば同じ方向に3回まわしたデータは、逆方向に1回だけまわしたデータと同じになります。上の図を見てみると、このケースで正しく1と答えている（横軸の3のところで、縦軸の値が3と1のところに結果が集中している）ようで素晴らしい（データ作成時にまわして戻す動作は除外したので、横軸の値が2のとことは縦軸が2のところだけに集中しています）。右に行くと上下のブレが大きくなって精度が出ていませんけど、これは、予測そのものが難しいことに加えて、学習データの正解が本当の正解ではない（たとえば、10回まわした結果だけど、本当は8回まわすだけで6面揃えられる）ためなのでしょうがない。あと、今回のプログラムのように90度まわすと1手と数える場合は最長でも26手で解けるらしいのですけど、縦軸の最大値が26近辺になっていてとても面白い。ルービック・キューブの真理に到達したのかもしれませんな。

さて、上のアニメーションを見ると、学習のたびに少しづつ良くなり続けているように見えますから、論文通りにデータ量を100億件まで増やせば更に精度が上がるのかもしれません。でも、論文では大量のコンピューター・リソースを使って36時間で学習を完了させてるけど、一般庶民の私はそんなスゴイ環境は持っていません……。さらに学習を続けるのは辛いので、このニューラル・ネットワークで続きをやることにしましょう。

そうそう、上の図で上下にピコピコして安定していないように見えるのは、ニューラル・ネットワークの最後のDense()のバイアス項の値が学習で変更されたためなので、無視してください。Dense()の引数にuseBias=Falseを入れておけばよかった……。誰かが、バイアス項を削除して、で、10日くらいかけて再学習してくれないかなぁ……。

今回の実装とDeepCubeA論文との差異

DeepCubeAの実装は公開されていて、その中にはTensorFlowのモデルが含まれています。だから、モデルをリバースすれば正確なニューラル・ネットワークが分かる……はずなのですけど、私のコンピューター上のTensorFlow2.0ではモデルを開けなかったので断念しました。コードの解析でも情報を得られるはずなのですけど、あまりにコードが複雑だったので速攻で断念。なので、たぶんニューラル・ネットワークの構造は論文と異なっています。それっぽい結果がでているので大きく間違えてはいないはずなのですけど、誰か調べてくれないかなぁ……。

論文では、AlphaGoのように、これまでに最も優秀な結果を出したニューラル・ネットワークと学習結果のニューラル・ネットワークを対戦させ、勝利した場合にニューラル・ネットワークを置き換えるやり方を採用しているのですけど、今回の実装ではやっていません。一応これには理由があって、AlphaGoの後継のAlphaZeroではやり方を変えていて、1つのニューラル・ネットワークをひたすら学習させたらしいから。私はこれを知らなかったので、過去に間違えた解説を書いています……。チャンピオン云々の部分を除けば概ね正しいと思うのだけど、誰かチェックしてくれないかなぁ……。

あと、上のコードの学習用データを生成するcreate_generator()関数の戻り値の関数ではルービック・キューブをまわす回数の最大値が31になっていますけど、論文では30でした。理由は単なる見落としです。でもまぁ、31でも多分あまり変わらないんじゃないかな。

最良優先探索で実際に解いてみる前に、論文を読んでみる

最良優先探索は前回の投稿で作成しましたので、同じ処理をPythonで書き直せば終わり……ではなくて、念のためにもう一度論文を眺めてみたら、論文の執筆者がBWAS（Batch Weighted A Star）と呼んでいるカスタマイズされたA*が使用されていました。といっても、最良優先探索のバリエーションでWikipediaにも説明があるA*からの変更点は、WeightedとBatchの2点だけ。以下、その変更点について述べます。

Weighted A*

A*（A Star）は最良優先探索のバリエーションで、評価関数を「これまでのコスト＋ゴールまでのコストの予測」として、ゴールまでのコストの予測が実際のコスト以下であることが保証された場合のアルゴリズムです。必ず最短経路が求められるというのが売りなのですけど、今回作成した深層学習の評価関数は「ゴールまでのコストの予測が実際のコスト以下である」ことを保証できていませんので、本当はA*じゃない……。でも、論文でA*と呼んでいるので以下A*でいきます。

さて、A*では、上で述べたように「これまでのコスト＋ゴールまでのコストの予測」が小さいものから順に探索を進めていきます。だから、「8歩進んで、たぶんあと2歩でゴールできると予測した状態」と「2歩進んで、たぶんあと8歩でゴールできると予測した状態」の優先度は同じです。でも、まだ2歩しか進んでいない後者の状態はこの先ものすごい数の状態を探索しなければならなそうで、できればあと2歩の前者の探索を優先したい気がします。でも、後者を完全に無視するのはやりすぎの気もするし……。

なので、「これまでのコスト」をいい感じに割り引くことにしましょう。たとえば、評価関数を「0.5×これまでのコスト＋ゴールまでのコストの予測」にしちゃう。最短経路にはならないかもしれないけれど、探索範囲が小さくなるから早く解がでますよね。これは重みを付けたとも表現できるので、Weighted A*と呼ばれています。

Batch Weighted A*

ニューラルネットワークを使用した予測は、計算量が大きいため、長い時間がかかります。でも、並列化できるという特徴もあるんです。GPU等を使うなら、1並列で実行する場合と100並列で実行する場合でも、処理時間はほぼ同じです。だからできるだけ並列で処理したい……のですけれど、普通のA*だと、キューから次の探索ノードを取得する部分が並列化の障害となります。

そこで、論文では、キューから指定した個数の状態を取得して、それぞれの次の状態への遷移をさせて、その後にまとめてゴールまでのコストを並列で予測するというやり方を提案しています。まとめて処理はバッチと呼ばれるので、Batch Weighted A*という名前になったわけですな。

で、このバッチの部分は、高速化だけではなく、解の精度とも関係します。たとえば、普通のA*のように、キューから最もコストが低い状態を取得して、で、その次の状態を予測したコストを計算した上でキューに入れたとします。A*で次に取得されるのは最もコストが小さい状態という縛りしかありませんから、今追加したばかりの状態が選ばれるかもしれません。でも、BatchがついたA*だと、追加は後回しになるのでバッチ処理開始時点で2番目にコストが小さい状態が必ず選ばれるというわけ。結果として、無駄は多くなるかもしれないけれど、探索範囲が広がるんです。

というわけで、Weightedで探索範囲を狭めて、Batchで高速化しつつ探索範囲を広げているのが、DeepCubeAが提案しているBatch Weighted A*です。今回は、このBatch Weighted A*を実装しましょう。

最良優先探索（Batch Weighted A*）で解いてみる

まぁ、そのBatch Weighted A*は、コードにするとえらいこと簡単なんだけどね……。こんな感じです。

from game  import *
from heapq import *


def get_answer(initial_state, cost_model, n, l):  # nはBatchの数で、lはWeightの大きさ。
    def get_next_state_and_next_answers():
        for _ in range(min(n, len(queue))):
            _, state, answer = heappop(queue)

            for action in ACTIONS.keys():
                next_state  = get_next_state(state, action)
                next_answer = answer + (action,)

                if next_state not in visited_states or visited_states[next_state] > len(next_answer):
                    visited_states[next_state] = len(next_answer)

                    yield next_state, next_answer

    queue = [(0, initial_state, ())]
    visited_states = {initial_state: 0}

    while queue:
        next_states, next_answers = zip(*get_next_state_and_next_answers())

        for next_state, next_answer in zip(next_states, next_answers):
            if next_state == GOAL_STATE:
                return next_answer

        cost_to_goals = cost_model.predict(np.array(tuple(map(get_x, next_states))), batch_size=10000).flatten()

        for next_state, next_answer, cost_to_goal in zip(next_states, next_answers, cost_to_goals):
            heappush(queue, (l * len(next_answer) + cost_to_goal, next_state, next_answer))

    return ()

まぁ、もともと最良優先探索のコードは簡単なわけだし、Batchを表現するためにget_next_state_and_next_answers()を加えて、Weightedを表現するためにコスト計算のところにl *を追加しただけだもんね。難しくなりようがない。

あ、上のコードの引数のcost_modelは、学習済みのKerasのニューラル・ネットワークで、model.predict()で予測を実行できます。cost_to_goalsに値を設定している部分ですな。

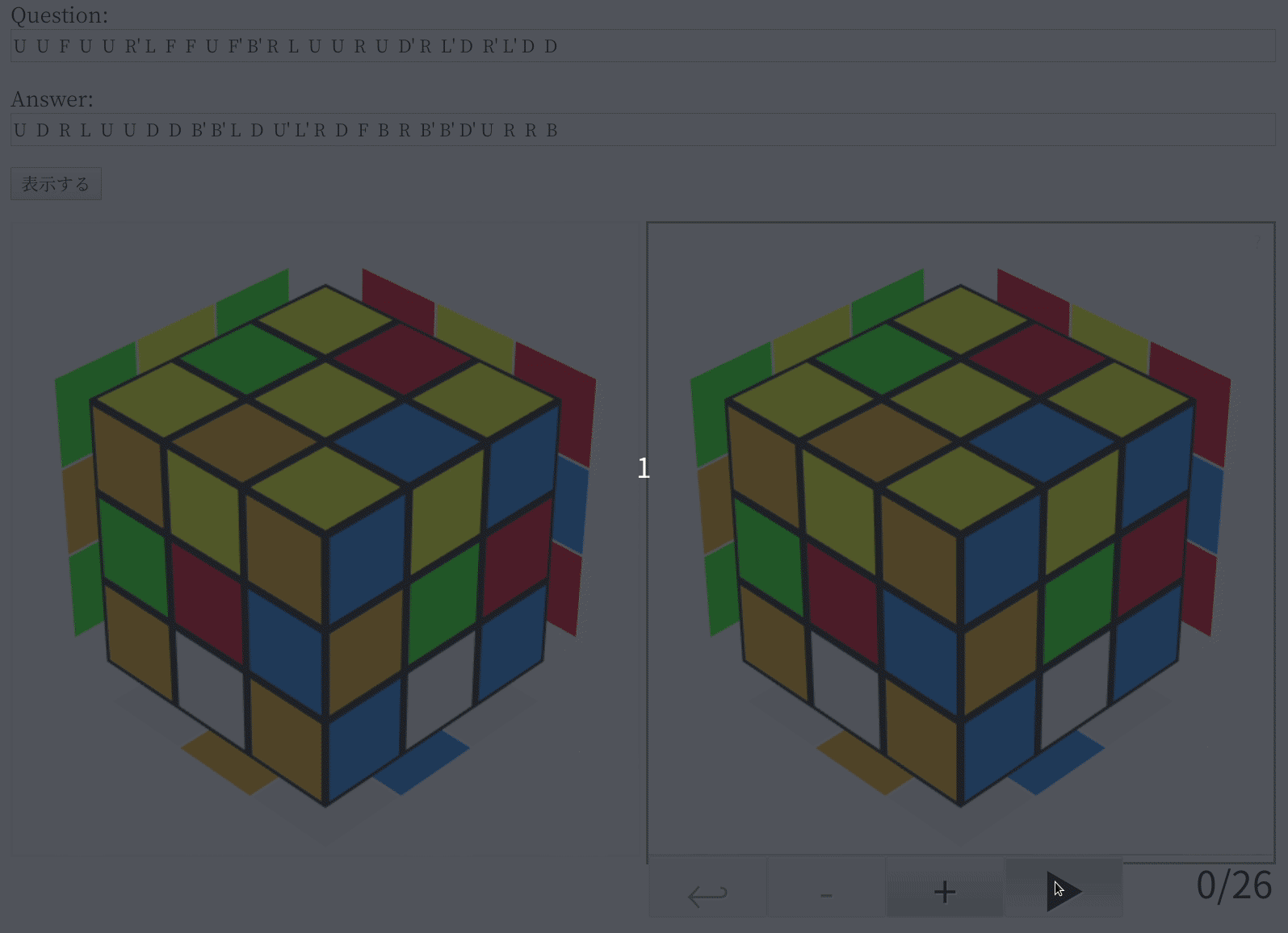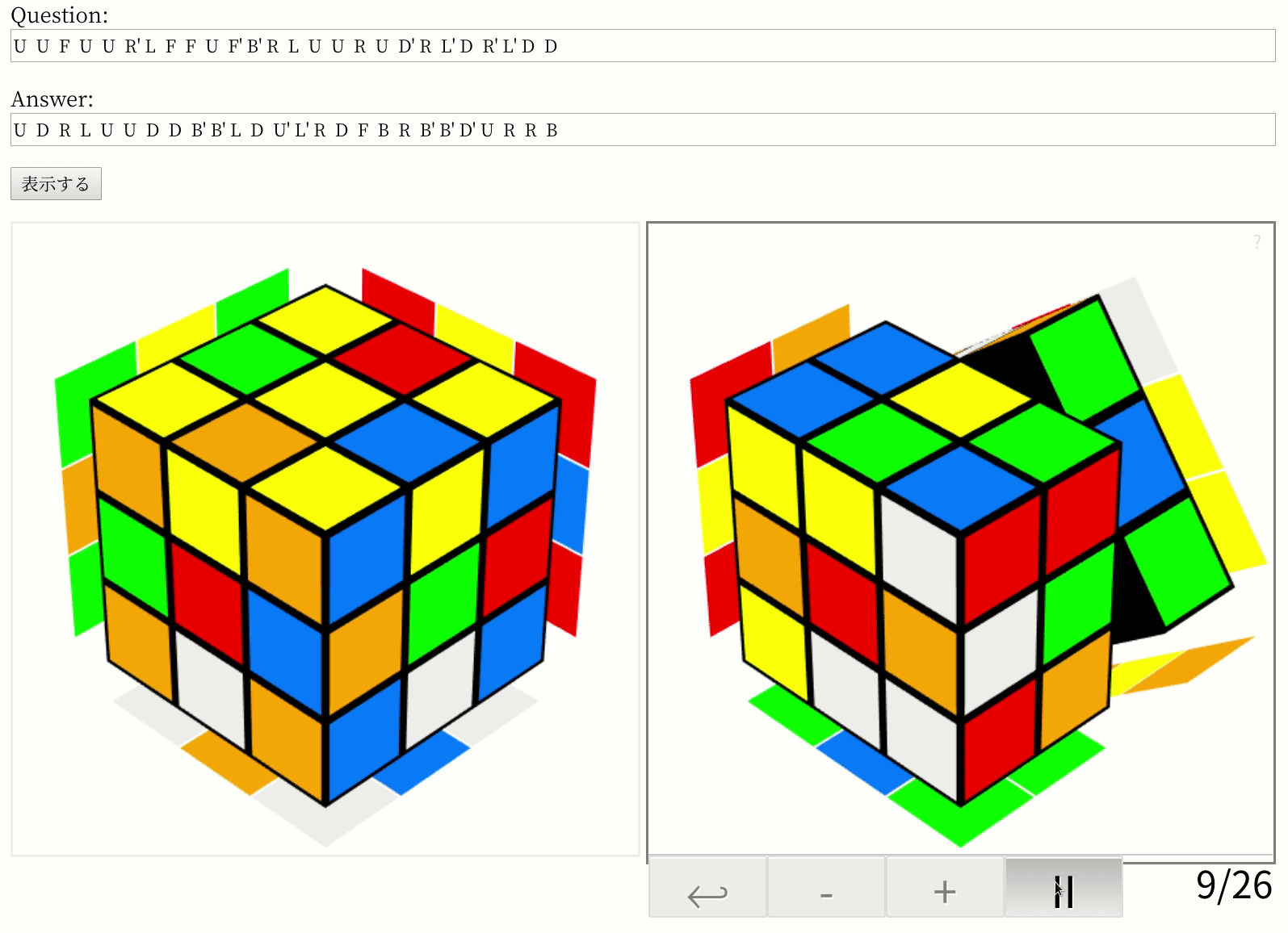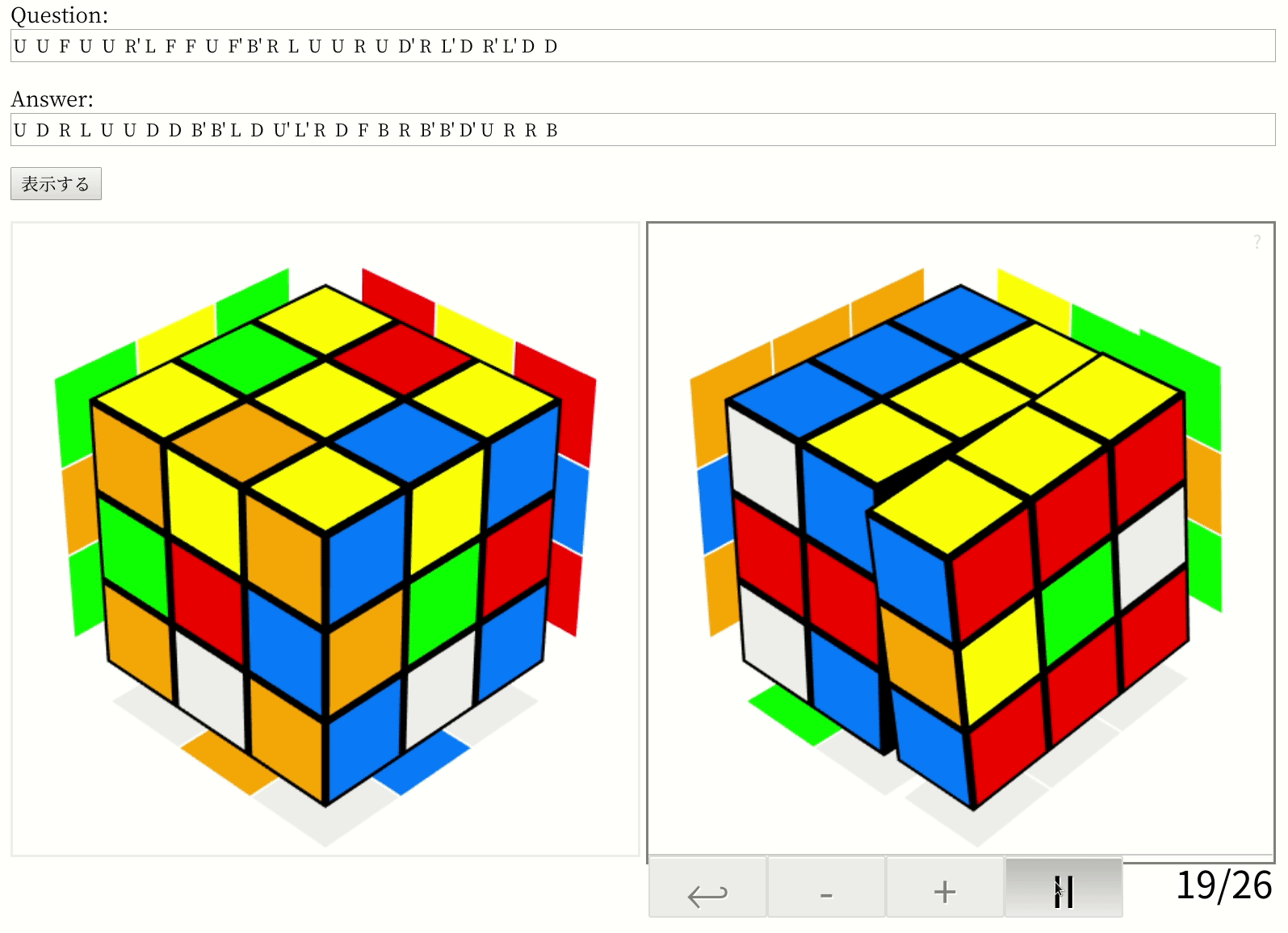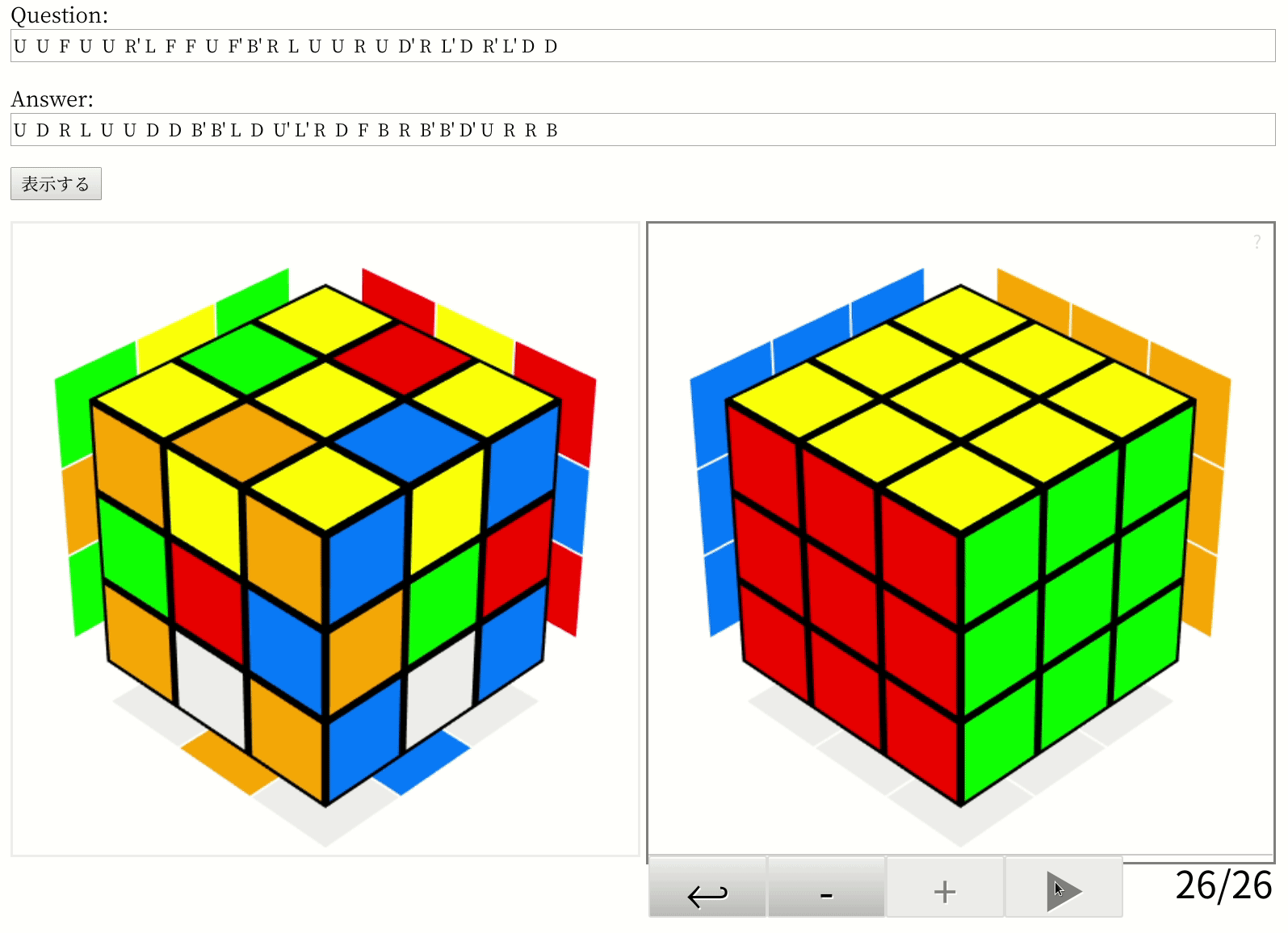
このコードを使って、論文が推奨しているパラメーター（n=10000、l=0.6）で最長手数である26手かかるルービック・キューブの問題（ルービック・キューブは20手で解けるというのは180度まわすのを1手と数える場合で、今回の実装のように90度まわす方式だと26手になるらしい）を解いてみたところ、みごとに最短手数の26手で解けました。私の環境（Core i5 + GeForce 1080 Ti、メモリ16GB）だと487秒もかかったけど……。

import batch_weighted_a_star
import tensorflow as tf

from game import *
from time import *


def main():
    model = tf.keras.models.load_model('model/cost.h5')

    question = "U U F U U R' L F F U F' B' R L U U R U D' R L' D R' L' D D".split(' ')

    state = GOAL_STATE

    for action in question:
        state = get_next_state(state, action)

    starting_time = time()

    answer = batch_weighted_a_star.get_answer(state, model, 10000, 0.6)  # 論文だと、最適解を出す場合はn=10000でl=0.6が良いらしい。

    print(f'{len(answer)} steps, {time() - starting_time:6.3f} seconds')
    print(' '.join(map(lambda action: action if len(action) == 2 else action + ' ', question)))
    print(' '.join(map(lambda action: action if len(action) == 2 else action + ' ', answer  )))

    tf.keras.backend.clear_session()

プログラムが出した答えは、こんな感じです。

ほら、最短の26手で解けてるでしょ？　まぁ、論文の実装でも最適解を出せるのは60.3%と書いてあるので、たまたまかもしれませんけどね。実際、25手の問題の一つでは最適解を逃して27手の解答を出しやがったし。

と、いうわけで

こんな簡単なコード（しかも深層学習の部分はほぼコピー＆ペースト）と民生用のGPUと10日間のダラダラで、今まで一度もルービック・キューブを解けたことがない私のプログラムがルービック・キューブを解けるんですから、最良優先探索と深層学習と、これらを見事に組み合わせてくれたDeepCubeAは素晴らしいですな。

論文によれば、同じやり方でスライドパズルや倉庫番とかも解けるらしい。たぶん、解けたら社会がさらに良くなるだろう、あの難しい問題もね。