Decompilation

The idea of decompiler is based on the fact that for each reducible graph we can always build an appropriate source code, as JavaScript has an ability to break any labeled block. Even if there wasn't such ability, we could emulate it with such construction: do { ... } while (false). So we just need to build a proper block hierarchy. Initially each block should start at the jump to label and end at the label itself. But due to some blocks may overlap, we should move the beginning of block to make them nest each other.

Another fact we should notice is that we can't express back jumps this way. Instead we should compute a loop forest of our CFG. But as we also can't jump inside loop, we should reorder CFG that all nodes, belonging to one loop come one after another. We can't let any non-loop nodes be inserted between loop nodes. So we end up with the following algorithm:

1. Build a CFG loop forest.
2. Perform a depth-first search over the CFG. When we are on some node, we should first visit its successors that exit the most outer loop, then we can visit the remaining ones (i.e. successors which stay on the same loop). Now the list has a topoligically sorted CFG, where no jumps into loops exist.
3. Add all the loops into the set of blocks.
4. For each jump instruction which does not follow a loop back edge add a block beginning at the instruction itself and ending at the node before the jump target label.
5. If two blocks overlap, move the later block's beginning before the beginnig of the earlier block.
6. Place blocks and while (true) loops, remove labels and remove all goto's that jump either the immideately following node or the previous node.
7. Replace remaining goto's with break's from the corresponding blocks.

Consider the following example:

function arrayCopy(arr, len) {
  $0:
    copy = new Array(len);
    copyLen = len;
    origLen = length(arr);
    if (copyLen > origLen) { goto $1; } else { goto $2; }
  $1:
    copyLen = origLen;
    goto $2;
  $2:
    i = 0;
    goto $3;
  $3:
    if (i < copyLen) { goto $4; } else { goto $5; }
  $4:
    elt = arr[i];
    copy[i] = elt;
    tmp = 1;
    i = i + tmp;
    goto $3;
  $5:
    return copy;
}

This is a pseudocode, which is very close to the real JavaScript, except for goto's. The pseudocode is obtained by direct translation of each model instruction into the corresponding JavaScript code. Here is our CFG:

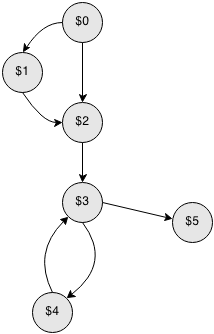
Out algorithm gives the following order: $0, $1, $2, $3, $4, $5. That is, in our example we have already properly ordered graph. The $5 node could follow after $3 if we didn't include additional requirement of visiting loop exits first. In that case we couldn't place block properly, as there would be a possible jump to $5 outside of the loop (but there is no in our example).

After we have ordered graph nodes, we can place blocks. The first block is { $3 $4 } as there is a loop with header is $3 and its last node is $4. Then we repeat block { $3 $4 } as there is jump from $3 to $5. But sinse there is already block { $3 $4 } we don't add it again. The last jump left is from $0 to $2, thus we add { $0 $1 } block. Finally, we have the following structure: { $0 $1 } $2 { $3 $4 } $5

Apply the 6th and 7th steps of our algorithm and get the following valid JavaScript code:

function arrayCopy(arr, len) {
  label2: {
// $0
    copy = new Array(len);
    copyLen = len;
    origLen = length(arr);
    if (copyLen > origLen) { /* goto $1; */ } else { break label2; /* goto $2; */ }
// $1
    copyLen = origLen;
    /* goto $2; */
  }
// $2:
  i = 0;
  /* goto $3; */
  label5: while (true) {
// $3:
    if (i < copyLen) { /* goto $4; */ } else { break label5; /* goto $5; */ }
// $4:
    elt = arr[i];
    copy[i] = elt;
    tmp = 1;
    i = i + tmp;
    /* goto $3; */
  }
// $5:
  return copy;

Optimizations

After building the AST this way we apply some optimizations over the AST, in order to make the resulting code more natural and neat. These optimizations have a practical reason too: they help to reduce the size of the generated JavaScript code in order to speed-up page loading.

Eliminating unnecessary breaks

When we have the following labelled block:

label: {
    A
    if (X) {
        B
        break label;
    }
    C
}

we can eliminate the break statement the following way:

label: {
   A
   if (X) {
      B
   } else {
      C
   }
}

of course, if all break statements have been eliminated eliminated, we can eliminate the whole block. For example, if there are no references to label1 in A, B and C, we could rewrite our example the following way:

A
if (X) {
   B
} else {
   C
}

Eliminating empty if clauses

Consider

if (X) {
    A
} else {
}

The else clause can be ommited:

if (X) {
    A
}

And the second case is

if (X) {
} else {
    A
}

can be transformed to

if (!X) {
    A
}

Nested if joining

The following code:

if (X) {
    if (Y) {
        A
    }
}

can be rewritten as

if (X && Y) {
    A
}

elseif composition

The code

if (X) {
    if (Y) {
        A
    } else {
        B
    }
} else {
    C
}

transformed to

if (!X) {
    C
} else if (Y) {
    A
} else {
    C
}

while condition merging

The following construction:

while (X) {
    if (Y) {
        break;
    }
    A
}

is transformed to

while (X && !Y) {
    A
}

Temporary variable elimination

For each usage of variable we can replace it by its declaration right-hand side, if this variable is used and declared once and the variable's usage follows immediately after its declaration.

Consider the following code:

a = foo()
b = bar()
c = a - b

We apply subtraction in left-to-right order. Thus, we should eliminate temporal declaration in backwards order, i.e. from right to left. Let us apply optimization:

a = foo()
c = a - bar();

and after the second application we have the following:

c = foo() - bar();

Notice, that we must always apply this optimization in the backwards computation order, as otherwise we may alter the method call order. And if these methods both have side effects, we loose the original meaning. Moreover, we can change the computation order in general, that leads to altering of liveness information. But as our register allocation and phi elimination relies in the original liveness information, we change our code meaning.

Applying optimizations example

Let's apply our optimizations to the example we introduced at the start of the section.

1. Apply empty if clause elimination to:

   if (copyLen > origLen) { } else { break label2; }

   and get

   if (copyLen <= origLen) { break label2; }

2. Eliminate unnecessary break in

   label2: {
       copy = new Array(len);
       copyLen = len;
       origLen = length(arr);
       if (copyLen <= origLen) { break label2; }
       copyLen = origLen;
   }

   and get

   label2: {
       copy = new Array(len);
       copyLen = len;
       origLen = length(arr);
       if (copyLen <= origLen) {
       } else {
           copyLen = origLen;
       }
   }

3. Eliminate unneccessary block and again apply empty if clause elimination to the previous code and get

   copy = new Array(len);
   copyLen = len;
   origLen = length(arr);
   if (copyLen > origLen) {
       copyLen = origLen;
   }

4. Apply temporary variable elimination to the code

   elt = arr[i];
   copy[i] = elt;

   and get

   copy[i] = arr[i];

and so forth. After all we end up with the following nice code:

function arrayCopy(arr, len) {
    copy = new Array(len);
    copyLen = len;
    origLen = length(arr);
    if (copyLen > origLen)
        copyLen = origLen;
    }
    i = 0;
    while (i < copyLen) {
        copy[i] = arr[i];
        i = i + 1;
    }
    return copy;
}

Applying registers

After AST optimizations TeaVM renames all variables to corresponding registers that are computed during the previous phase. If only we renamed variables at the previous phase, we loose information abount the number of usages.