Skip to content

Multiple GPUs and machines

Jump to bottom Edit New page
Chris Basoglu edited this page Sep 1, 2016 · 46 revisions

1. Introduction

CNTK currently supports three parallel SGD algorithms:

  1. DataParallelSGD
  2. BlockMomentumSGD
  3. ModelAveragingSGD
Notes on SGD Algorithm implementations location and licensing.

As explained in the corresponding Wiki section the complete CNTK has two licenses, that applicable to different components of the kit:

The second license is specific for the 1-bit Stochastic Gradient Descent (1bit-SGD) and Block-Momentum components and is more restrictive than the main CNTK license.

Data-Parallel SGD may be used with or without 1bit-SGD. When Data-Parallel SGD is used without 1bit-SGD, it is licensed under the main CNTK License. When it is used with 1bit-SGD, it is licensed under the CNTK 1bit-SGD License.

Block-Momentum SGD is always licensed under the CNTK 1bit-SGD License irrespective of the usage scenario. Note, that to obtain the source code implementation for this algorithm, you need to follow the instructions for enabling 1bit-SGD even if you do not plan to use 1bit-SGD itself.

Model-Averaging SGD's implementation is stored with the main CNTK code and is licensed under the main CNTK License.

2. Configuring Parallel Training in CNTK

To enable parallel training in CNTK, it is first necessary to turn on the following switch in either the configuration file or in the command line:

parallelTrain = true

Secondly, the SGD block in the config file should contain a sub-block named ParallelTrain with the following arguments:

  1. parallelizationMethod: (mandatory) legitimate values are DataParallelSGD, BlockMomentumSGD, and ModelAveragingSGD.

    This specifies which parallel algorithm to be used.

  2. distributedMBReading : (optional) accepts Boolean value: true or false; default is false

    It is recommended to turn distributed minibatch reading on to minimize the I/O cost in each worker. If you are using CNTK Text Format reader, Image Reader, or Composite Data Reader, distributedMBReading should be set to true.

  3. parallelizationStartEpoch: (optional) accepts integer value; default is 1.

    This specifies starting from which epoch, parallel training algorithms are used; before that all the workers doing the same training, but only one worker is allowed to save the model. This option can be useful if parallel training requires some "warm-start" stage.

  4. syncPerfStats: (optional) accepts integer value; default is 0.

    This specifies how frequently the performance statistics will be printed out. Those statistics includes the time spent on communication and/or computation in a synchronization period, which can be useful to understand the bottleneck of parallel training algorithms.

    0 means no statistics will be printed out. Other values specifies how often the statistics will be printed out. For example, syncPerfStats=5 means statistics will be printed out after every 5 synchronizations.

  5. A sub-block which specifies details of each parallel training algorithm. The name of the sub-block should equal to parallelizationMethod. (mandatory)

2.1 Data-Parallel Training with 1-bit SGD

CNTK implements the 1-bit SGD technique [1]. This technique allows to distribute each minibatch over K workers. The resulting partial gradients are then exchanged and aggregated after each minibatch. "1 bit" refers to a technique developed at Microsoft for reducing the amount of data that is exchanged for each gradient value to a single bit.

2.1.1 The "1-bit SGD" Algorithm

Directly exchanging partial gradients after each minibatch requires prohibitive communication bandwidth. To address this, 1-bit SGD aggressively quantizes each gradient value... to a single bit (!) per value. Practically, this means that large gradient values are clipped, while small values are artificially inflated. Amazingly, this does not harm convergence if, and only if, a trick is used.

The trick is that for each minibatch, the algorithm compares the quantized gradients (that are exchanged between workers) with the original gradient values (that were supposed to be exchanged). The difference between the two (the quantization error) is computed and remembered as the residual. This residual is then added to the next minibatch.

As a consequence, despite the aggressive quantization, each gradient value is eventually exchanged with full accuracy; just at a delay. Experiments show that, as long as this model is combined with a warm start (a seed model trained on a small subset of the training data without parallelization), this technique has shown to lead to no or very small loss of accuracy, while allowing a speed-up not too far from linear (the limiting factor being that GPUs become inefficient when computing on too small sub-batches).

For maximum effeciency, the technique should be combined with automatic minibatch scaling, where every now and then, the trainer tries to increase the minibatch size. Evaluating on a small subset of the upcoming epoch of data, the trainer will select the largest minibatch size that does not harm convergence. Here, it comes in handy that CNTK specifies the learning rate and momentum hyperparameters in a minibatch-size agnostic way.

2.1.2 Using 1-bit SGD

1-bit SGD itself has no parameter other than enabling it and after which epoch it should commence. In addition, automatic minibatch-scaling should be enabled. These are configured by adding the following parameters to the SGD block:

SGD = [
    ...
    ParallelTrain = [ 
        DataParallelSGD = [
            gradientBits = 1
        ]
        parallelizationStartEpoch = 2  # warm start: don't use 1-bit SGD for first epoch
    ]
    AutoAdjust = [
        autoAdjustMinibatch = true       # enable automatic growing of minibatch size
        minibatchSizeTuningFrequency = 3 # try to enlarge after this many epochs
    ]
]

Note that Data-Parallel SGD can also be used without 1-bit quantization. However, in typical scenarios, especially scenarios in which each model parameter is applied only once like for a feed-forward DNN, this will not be efficient due to high communication-bandwidth needs.

Section 2.2.3 below shows results of 1-bit SGD on a speech task, comparing with the Block-Momentum SGD method which is described next. Both methods have no or nearly no loss of accuracy at near-linear speed-up.

2.2 Block-Momentum SGD

Block-Momentum SGD is the implementation of the "blockwise model update and filtering", or BMUF, algorithm, short Block Momentum [2].

2.2.1 The Block-Momentum SGD Algorithm

The following figure summarizes the procedure in the Block-Momentum algorithm.

bm

2.2.2 Configuring Block-Momentum SGD

To use Block-Momentum SGD, it is required to have a sub-block named BlockMomentumSGD in the SGD block with the following options:

  1. syncPeriod. This is similar to the syncPeriod in ModelAveragingSGD, which specifies how frequent a model synchronization is performed. The default value for BlockMomentumSGD is 120,000.

  2. resetSGDMomentum. This means after every synchronization point, the smoothed gradient used in local SGD will be set as 0. The default value of this variable is true.

  3. useNesterovMomentum. This means the Nesterov-style momentum update is applied on the block level. See [2] for more details. The default value of this variable is true.

The block momentum and block learning rate are usually automatically set according to the number of workers used, i.e.,

block_momentum = 1.0 - 1.0/num_of_workers
block_learning_rate = 1.0

Our experience indicates that these settings often yield similar convergence as the standard SGD algorithm up to 64 GPUs, which is the largest experiment we performed. It is also possible to manually specify the these parameters using the following options:

  • blockMomentumAsTimeConstant specifies the time constant of the low-pass filter in block-level model update. It is calculated as:

    blockMomentumAsTimeConstant = -syncPeriod / log(block_momentum)
# or inversely 
block_momentum = exp(-syncPeriod/blockMomentumAsTimeConstant)

  • blockLearningRate specifies the block learning rate.

Following is an example of Block-Momentum SGD configuration section:

learningRatesPerSample=0.0005
# 0.0005 is the optimal learning rate for single-GPU training. 
# Use it for BlockMomentumSGD as well 
ParallelTrain = [
    parallelizationMethod = BlockMomentumSGD
    distributedMBReading = true
    syncPerfStats = 5
    BlockMomentumSGD=[
        syncPeriod = 120000
        resetSGDMomentum = true
        useNesterovMomentum = true
    ]
]

2.2.3 Using Block-Momentum SGD

1. Re-tuning learning parameters

  • To achieve similar throughput per worker, it is necessary to increase the number of samples in a minibatch proportional to the number of workers. This can be achieved by adjusting minibatchSize or nbruttsineachrecurrentiter, depending on whether frame-mode randomization is used.

  • There is no need to adjust the learning rate (unlike Model-Averaging SGD, see below).

  • It is recommended to using Block-Momentum SGD with a warm started model. On our speech recognition tasks, reasonable convergence is achieved when starting from seed models trained on 24 hours (8.6 million samples) to 120 hours (43.2 million samples) data using standard SGD.

2. ASR experiments

We used the Block-Momentum SGD and the Data-Parallel (1-bit) SGD algorithms to train DNNs and LSTMs on a 2600 hours speech-recognition task, and compared word recognition accuracies vs. speed-up factors. The following tables and figures shows the results (*).

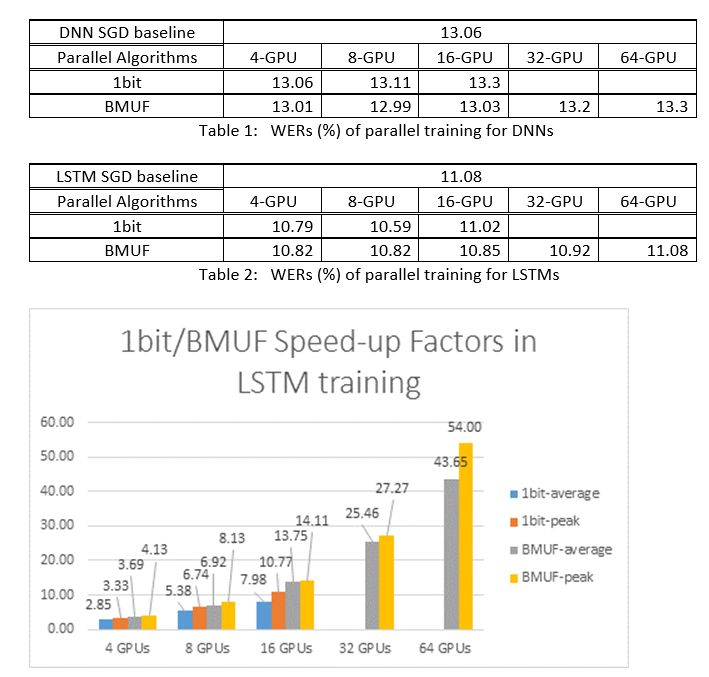
compare

(*): Peak speed-up factor: for 1-bit SGD, measured by the maximum speed-up factor (compared with SGD baseline) achieved in one minibatch; for Block Momentum, measured by the maximum speed-up achieved in one block; Average speed-up factor: the elapsed time in SGD baseline divided by the observed elapsed time. These two metrics are introduced due to the latency in I/O can greatly affect the average speed-up factor measurement, especially when the synchronization is performed at the mini-batch level. At the same time the maximum speed-up factor is relatively robust.

3. Caveats

  • It is recommended to set resetSGDMomentum to true; otherwise it often leads to divergence of training criterion. Resetting SGD momentum to 0 after every model synchronization essentially cuts off the contribution from the last minibatches. Therefore, it is recommended not to use a large SGD momentum. For example, for a syncPeriod of 120,000, we observe a significant accuracy loss if the momentum used for SGD is 0.99. Reducing the SGD momentum to 0.9, 0.5 or even disabling it altogether gives similar accuracies as the one can achieved by the standard SGD algorithm.

  • Block-Momentum SGD delays and distributes model updates from one block across subsequent blocks. Therefore, it is necessary to make sure that model synchronizations is performed often enough in the training. A quick check is to use blockMomentumAsTimeConstant. It is recommended that the number of unique training samples, N, should satisfy the following equation:

    N >= blockMomentumAsTimeConstant * num_of_workers ~= syncPeriod * num_of_workers^2

The approximation stems from the following facts: (1) Block Momentum is often set as (1-1/num_of_workers); (2) log(1-1/num_of_workers)~=-num_of_workers.

2.3 Model-Averaging SGD

Model-Averaging SGD is an implementation of the model averaging algorithm detailed in [3,4] without the use of natural gradient. The idea here is to let each worker processes a subset of data, but averaging the model parameters from each worker after a specified period.

Model-Averaging SGD generally converges more slowly and to a worse optimum, compared to 1-bit SGD and Block-Momentum SGD, so it is no longer recommended.

To use Model-Averaging SGD, it is required to have a sub-block named ModelAveragingSGD in the SGD block with the following options:

  • syncPeriod specifies the number of samples that each worker need to process before a model averaging is conducted. The default value is 40,000.

2.3.1 Using Model-Averaging SGD

To make Model-Averaging SGD maximally effective and efficient, users need to tune some hyper-parameters:

  • minibatchSize or nbruttsineachrecurrentiter. Suppose n workers are participating in the Model-Averaging SGD configuration, the current distributed reading implementation will load 1/n-th of the minibatch into each worker. Therefore, to make sure each worker produces the same throughput as the standard SGD, it is necessary to enlarge the minibatch size n-fold. For models that are trained using frame-mode randomization, this can be achieved by enlarging minibatchSize by n times; for models are trained using sequence-mode randomization, such as RNNs, some readers require to instead increase nbruttsineachrecurrentiter by n.

  • learningRatesPerSample. Our experience indicates that to get similar convergence as the standard SGD, it is necessary to increase the learningRatesPerSample by n times. An explanation can be found in [2]. Since the learning rate is increased, an extra care is needed to make sure the training does not diverge--and this is in fact the main caveat of Model-Averaging SGD. You can use the AutoAdjust settings to reload the previous best model if an increase in training criterion is observed.

  • warm start. It is found that Model-Averaging SGD usually converges better if it is started from a seed model which is trained by the standard SGD algorithm (without parallelization). On our speech recognition tasks, reasonable convergence is achieved when starting from seed models trained on 24 hours (8.6 million samples) to 120 hours (43.2 million samples) data using standard SGD.

The following is an example of ModelAveragingSGD configuration section:

learningRatesPerSample = 0.002
# increase the learning rate by 4 times for 4-GPU training. 
# learningRatesPerSample = 0.0005
# 0.0005 is the optimal learning rate for single-GPU training.
ParallelTrain = [
    parallelizationMethod = ModelAveragingSGD
    distributedMBReading = true
    syncPerfStats = 20
    ModelAveragingSGD = [
        syncPeriod=40000
    ]
]

3. Running Parallel Training with CNTK

Parallelization in CNTK is implemented with MPI. Given any of the parallel-training configurations above, the following command can be used to start a parallel MPI job:

  • Parallel training on the same machine with Linux:

    mpiexec --npernode $num_workers  $cntk  configFile=$config

  • Parallel training on the same machine with Windows:

    mpiexec -n %num_workers%  %cntk%  configFile=%config%

  • Parallel training across multiple computing nodes with Linux:

    Step 1: Create a host file $hostfile using your favorite editor

    # Comments are allowed after pound sign
name_of_node1 slots=4 # we want 4 workers on node1
name_of_node2 slots=2 # we want 2 workers on node2

    Step 2: Execute your workload

    mpiexec -hostfile $hostfile  ...  $cntk  configFile=$config

  • Parallel training across multiple computing nodes with Windows:

    mpiexec --hosts %num_nodes% %name_of_node1% %num_workers_on_node1%  ...  %cntk%  configFile=%config%

where $cntk should refer to the path of the CNTK executable ($x is the Linux shell's way of substituting environment variables, the equivalent of %x% in the Windows shell).

References

[1] F. Seide, Hao Fu, Jasha Droppo, Gang Li, and Dong Yu, "1-bit stochastic gradient descent and its application to data-parallel distributed training of speech DNNs," in Proceedings of Interspeech, 2014.

[2] K. Chen and Q. Huo, "Scalable training of deep learning machines by incremental block training with intra-block parallel optimization and blockwise model-update filtering," in Proceedings of ICASSP, 2016.

[3] M. Zinkevich, M. Weimer, L. Li, and A. J. Smola, "Parallelized stochastic gradient descent," in Proceedings of Advances in NIPS, 2010, pp. 2595–2603.

[4] D. Povey, X. Zhang, and S. Khudanpur, "Parallel training of DNNs with natural gradient and parameter averaging," in Proceedings of the International Conference on Learning Representations, 2014.

Add a custom footer

Getting Started

Additional Documentation

How to use CNTK

Using CNTK Models in Your Code

Advanced topics

Licenses

Source Code & Development

Clone this wiki locally